Energy of motion?

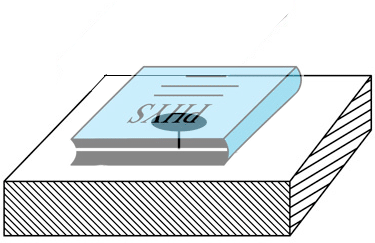A heavy enough book resting on a tack has enough gravitational energy to do work on the tack and push it in to the floor.

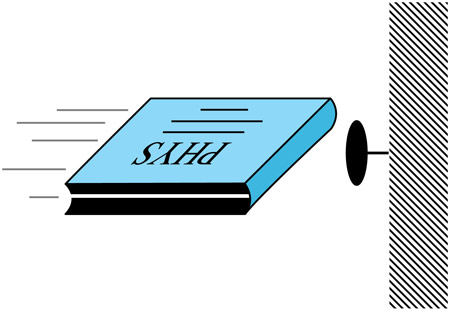But there are other ways to do work, for example, throwing a book at a tack...

Isn't the book in this case also "doing work on the tack"?

What measurable characteristics of the moving book is this related to if it's an energy??

Questions about dropping books

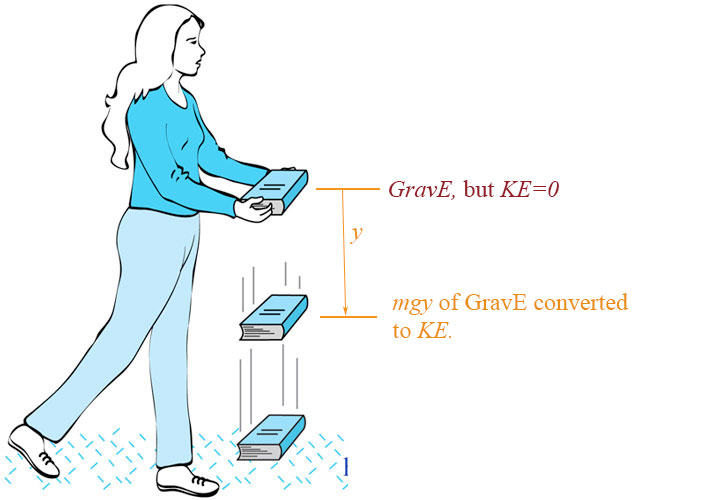
If, instead of lowering a book slowly, and letting it do work on a hand, consider just letting the book drop...

Before the book hits anything... The book should be losing gravitational energy ($mgh$) as it drops.

Where does this gravitational energy "go"?

According to the hypothesis of energy conservation, the book's gravitational energy was converted into another kind of energy, energy of motion: kinetic energy of the book.

As one kind of energy (gravitational) was reduced, another kind (kinetic) increased.

Getting quantitative about kinetic energy

Here are some candidate formulas for kinetic energy ($k$ is a proportionality constant):

• K.E. = $k \frac{v}{m}$
• K.E. = $k \frac{m} {\sqrt{v}}$
• K.E. = $k \frac{m}{v^2}$
• K.E. = $k\cdot m\cdot v$
• K.E. = $k\cdot m \cdot \sqrt{v}$
• K.E. = $k\frac{m}{v}$
• K.E. = $k\cdot m \cdot v^2$

In your experiments with dropping balls, you have already gathered enough data to figure out how the dependence of kinetic energy on velocity if we assume that energy conservation is true:

Energy Conservation

The hypothesis of energy conservation says that:

• If you add up all the kinds of energy that an object has--call this its total energy, $E$,
• The energy might change from one form to another, but
• The total energy, $E$, remains the same.

Consider the total energy of the dropped book being the sum of it's GravE and K.E. Than as the object *loses* GravE (that is, as it drops), what needs to happen to its K.E.?

If K.E. increases as an object drops,

• Let's measure $y$ as the distance below the point at which an object was dropped, so that it's a positive number. But remember, because $y$ is pointed down, the ball is actually *losing* energy as $y$ increases.
• Measure $v$ to be positive in the downward direction.

So energy conservation says: $$\begineq \text{GravE lost} &=& \text{Kinetic E gained}\\ mgy &=&KE(y) \endeq $$

We need to think about how we expect the function $v(y)$ to behave. We'll consider the 3 possibilities:

1. K.E.=$kmv^2$
2. K.E.=$kmv$
3. K.E.=$km\sqrt v$

Now go ahead...

1. Solve each equation to find how the speed should depend on how far the book has dropped: $v(y)$.
2. Make a sketch of roughly how each $v(y)$ should behave (you can use Wolfram Alpha to try out different functions).

and we'll see which way nature seems to work...

 

Expectations and outcomes

So if the gravitational energy that the dropping book loses as it drops a distance $y$ below its starting point is $mgy$,

...and that energy shows up as a gain in kinetic energy, $$\begineq \text{KE gained} &=& \text{GravE lost}\\ \text{KE gained} &=& mgy \endeq $$

Then here are our 3 scenarios for different K.E. expressions:

KE=$kmv^2$	KE=$kmv$	KE=$km\sqrt{v}$
	$$\begineq kmv &=& mgy\\ v&=& \frac{g}{k}y\\ \endeq$$
Plots of $v(y)$ vs $y$...
>

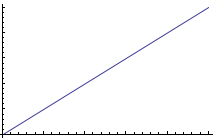Here's a spreadsheet with data from a video of a dropping ball which we'll use to decide...