Characterizing vector fields
*Some* vector fields, $\myv F$, represent the gradient of a function, $\myv F=\myv \grad f$.
In the next few class sessions we'll be trying to figure out:
- How to tell if a vector field, $\myv F(x,y)$, is the gradient of a function,
- How to find a function $f$, such that $\myv \grad f=\myv F$.
- How this makes some line integrals *a lot* easier to evaluate.
- Line integrals?!? Oh yeah, we haven't talked about those yet! We'll also find out what a line integral is, and how to calculate it.
Gradients
The gradient of a scalar field is a vector field. $$ \myv \grad f(x,y)=f_x(x,y)\uv i+f_y(x,y)\uv j=\myv v(x,y)$$
$$\myv \grad f(x,y,z)=f_x(x,y,z)\uv i+f_y(x,y,z)\uv j+f_z(x,y,z)\uv k=\myv v(x,y,z)$$
Gradient Fields
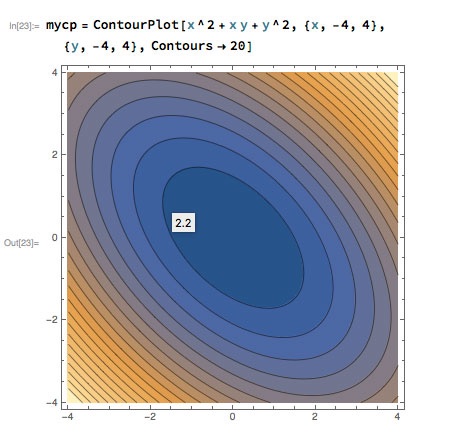
Some (but not all) vector fields are gradient fields. Consider $f(x,y)=x^2+xy+y^2$. The gradient is $$\myv \grad f=\langle f_x,f_y \rangle = (2x+y)\uv i+ (2y+x)\uv j.$$
The contour plot of $f(x,y)$ is shown below. Based on the contour plot what can you say about the vector field $\myv v(x,y) = \myv \grad f$ (which is *not* shown below)?
- The direction of the vectors?
- Where are the vectors longer or shorter?
Grad / Contour example
Grad / Contour example

Grad / Contour example
Conservative fields & potential functions
Consider the vector field... $$\myv F(x,y)=2x\uv i+y\uv j$$
Can you guess a function $f(x,y)$ such that $$\myv F(x,y) = \myv \grad f(x,y)?$$ In other words, what single function, $f(x,y)$ has partial derivatives $f_x=2x$ and $f_y=y$?
If a function $f$ exists such that $\myv F(x,y)=\myv \grad f(x,y)$:
- $\myv F(x,y)$ is a conservative vector field.
- $f(x,y)$ is called a potential function for the vector field $\myv F$.
Another one
Consider the vector field... $$\myv F(x,y)=-y\uv i+2x\uv j$$
Can you guess a function $f(x,y)$ such that $$\myv F(x,y) = \myv \grad f(x,y)?$$ In other words, what function, $f(x,y)$ has partial derivatives $f_x=-y$ and $f_y=2x$?
Conservative vector fields and Clairaut
At this point, we typically start writing the components of *any* 2-d vector field as $$\myv F(x,y)=P(x,y)\uv i+Q(x,y)\uv j.$$
If $\myv F$ is a conservative vector field then there exists a (scalar) potential function $f$, such that: $$\begineq \myv F=\myv \grad f&=f_x\uv i +f_y\uv j\\ &\equiv P\uv i+Q\uv j \endeq$$
According to Clairaut's theorem, for any continuous function on a closed domain, $f_{xy}=f_{yz}\Rightarrow P_y=Q_x$. So in terms of $P$ and $Q$, we have this way of detecting conservative functions:
Cross-derivative test Consider a function $\myv F(x,y)=P(x,y)\uv i+Q(x,y)\uv j$. The vector field $\myv F$ is conservative if $$\frac{\del P(x,y)}{\del y} = \frac{\del Q(x,y)}{\del x}.$$
Apply the cross-derivative test to $\myv F=\myc{2x,-y}$ and $\myv G=\myc{-y,2x}$
In Thermodynamics you'll use some implications of this idea to distinguish between functions (rather than vector fields) which are potential functions and those which are not. We'll find that energy and entropy are "potential functions". But work and heat are *not*.
Notes for homework
- The position vector of a point is defined to be $\myv r(x,y)=\myc{ x, y }$. At any point in space it is pointing away from the origin--it is a radial vector.
- The unit radial vector--$\uv r$ or $\hat{e}_r$--is the same as the unit position vector: $$\uv r=\frac{\myv r}{|\myv r|}=\frac{x\uv i}{\sqrt{x^2+y^2}} +\frac{y\uv j}{\sqrt{x^2+y^2}}$$