Landscapes, surfaces, and gradient fields

The function, $z=f(x,y)$, can be graphed as a surface. We can imagine ourselves on such a surface: $z$ corresponds to the altitude of Earth's surface above sea level, and varies as we move East or West (in the $+x$ or $-x$ direction) or North-South ($\pm y$).
What you already know about the gradient
For a smoothly varying, continuous surface, $z=f(x,y)$, we can calculate the gradient everywhere, $$\myv F(x,y)=\myv \grad f(x,y)=f_x(x,y) \uv i+f_y(x,y)\uv j.$$ The gradient is a vector function and it has these characteristics:
- At any location $(x,y)$, the gradient always points in the direction to go, if you want to go up as steeply as possible at that point.
- The gradient is always perpendicular to contour lines of the surface $f$,
- The magnitude of the gradient is the slope of the surface $f$ in that direction of steepest increase.
The question is... Is every vector field the gradient of some surface? of some continuous surface? To answer this, you'll try to imagine the surfaces that correspond to different vector fields.
Read the following stories, written as hiking journal entries, with corresponding diagrams of 2-d vector fields. Do both of these stories describe plausible surfaces that you could hike on??
June 14 entry
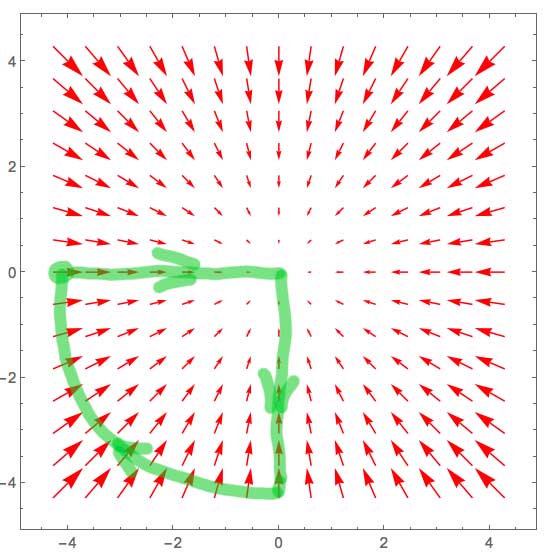 Here's what I wrote in my hiking journal about the hike I took on the surface with these gradient vectors (above):
Here's what I wrote in my hiking journal about the hike I took on the surface with these gradient vectors (above):
-
I awoke early on the side of what appeared to be a mighty mountain peak. I left my camp (the big green dot) headed East. The path, though initially quite steep, gradually flattened out until I found myself at the top, in the middle of a fairly flat meadow, after hiking about 4 miles.
I decided to go back a different way and started hiked south. At first the path was flat, then a mild down hill, but it kept getting steeper and I descended ever faster. After I had gone about 4 miles, pretty much all downhill, my altimeter told me I had reached the altitude of my camp.
I turned West, and "contoured" at a constant height, clockwise around the peak, until I reached my camp again.
I was famished and had a delicious meal of sardines with crackers and cheese.
June 18 entry
Another entry, corresponding to a different diagram of gradient vectors.
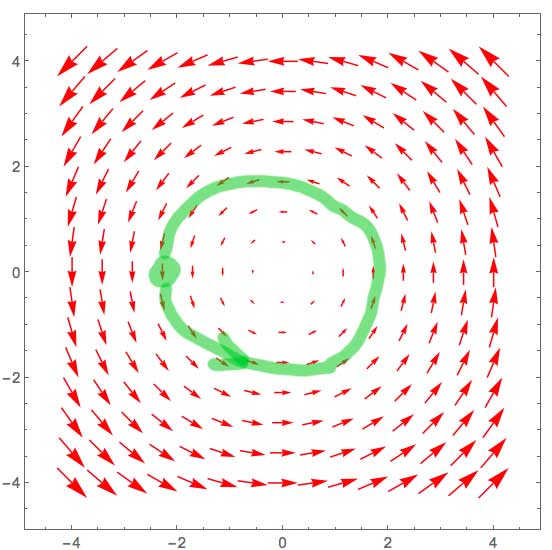 Here is a different entry from my hiking journal
Here is a different entry from my hiking journal
June 18, 2014 - This being new country to me, I didn't know exactly what to expect. Being in possession of a GPS unit, I figured I could hike for a while and eventually find my way back to camp. So, marking the location of my camp, I left camp in a southerly direction, going uphill at first, so as to have an easier time of it later in the day on the way back to camp.
Just a few steps away from my campsite, behind a grove of trees, I found another tent! I met "Ted" who was just getting up, and looked like he was preparing a big breakfast. His plan was to hike North. I waved goodbye and continued on my way.
I went uphill at a steady climb. I kept turning left, little by little (at first towards the East) to keep going up hill at a steady pace. If I had gone straight, I would have found myself going uphill *very* steeply. I continued to climb steadily.
After about 2 hours, I was surprised to see Ted bounding downhill towards me through the woods. He was moving so fast, that we barely had to time to wave at each other before he was gone.
By lunchtime, my GPS told me that I had followed an arc, and was about half-way around a roughly circular path that would eventually take me back to camp.
After lunch, I climbed steadily once more, always as nearly uphill as I could. The flora and fauna were new to me, and looked like something that I vaguely recalled from a painting. I continued for several more hours uphill, until I finally stumbled into camp, after sunset, exhausted. I never did get to go downhill all day!
I heard loud snoring from Ted's tent. I ate a supper of dried ramen noodles without bothering to cook them and fell into a deep sleep.
Respond to these questions
...on Moodle.
- Do both of both of these stories tell equally plausible tales about a hike, or not? Which one is more (or which one is less) plausible?
- Based on the diagrams and accounts... did either hiker go over a sharp ridge or cliff, or encounter some other discontinuity in the landscape?
- When the hiker ended up back at camp (at least, at the same latitude and longitude, according to his GPS) could he have arrived at the same altitude as when he started? Answer this for both hikes.
- What do you conclude about the question of whether all vector fields represent gradient fields of a real surface?
- Questions or things you wondered about?
Here is a real surface which allows you to walk in a circle and always go downhill:

The part that we're walking on is continuous
Such a surface can be continuous. I can follow a circular path (going always downhill) and return to the same latitude and longitude I started from. However I will be at a different altitude from where I started!
For any given latitude and longitude $(x,y)$ position, there is more than one possible altitude. But a function always returns a unique height/altitude for any given input tuple of $(x,y)$. Therefore the surface does not represent a function.
Photo credits: Joshua Ganderson