Fundamental Theorem: Conservative Vector Fields

Fundament = Foundation

• We'll tie together 3 characteristics of conservative vector fields
• and find an easy way to calculate a vector path integral if the vector field is conservative.

Conservative vector field

Cross-derivative test

Consider a function $\myv F(x,y)=P(x,y)\uv i+Q(x,y)\uv j$. The vector field $\myv F$ is conservative if $$\frac{\del P(x,y)}{\del y} = \frac{\del Q(x,y)}{\del x}.$$

Path independence

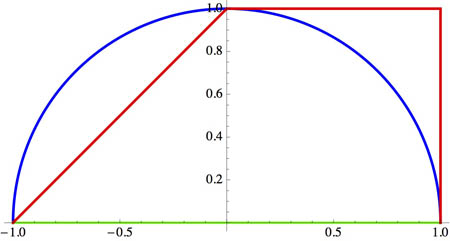In general, the value of a line integral of a given vector function depends, not only on the endpoints, but also on which path is taken.

For the integrals above, we found: $$\color{blue}{\int_\text{blue}\myv F\cdot \myv r=0},$$ $$\color{red}{\int_\text{red}\myv F\cdot \myv r=-\frac 23 },$$ $$\color{green}{\int_\text{green}\myv F\cdot \myv r=0}.$$

These line integrals--all sharing the same initial and final points--give different values depending on which path is taken.

But there exists a class of vector fields for which the path taken when calculating vector integrals does not matter. The only things that do matter are the starting and ending point.

This characteristic might remind you of the...

Fundamental Theorem - single variable calculus

The fundamental theorem of calculus for a single variable: $$\int_a^b \frac{df(x)}{dx}\,dx=\left.f(x)\right|^{x=b}_a=f(b)-f(a)$$ where $\frac{df(x)}{dx}$ is continuous on $[a,b]$.

The integral of [the derivative of $f$] only depends on the values of $f$ at the endpoints of the interval.

Vector integral of a conservative field

$\myv F$ is a conservative vector field, if a potential function, $f$, exists such that $\myv F$ is the gradient of $f$: $\myv F(x,y,z)=\myv \grad f(x,y,z)=\langle \frac{\del f}{\del x}, \frac{\del f}{\del y}, \frac{\del f}{\del z}\rangle$

Integrate it... $$\begineq \int_C\myv F\cdot d\myv r &= \int_C(\myv\grad f)\cdot d\myv r = \int_{t=a}^b (\myv\grad f(\myv r(t))\cdot \myv r'(t)\,dt \\ &=\int_{t=a}^b \langle \frac{\del f}{\del x}, \frac{\del f}{\del y}, \frac{\del f}{\del z}\rangle \cdot \langle \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt}\rangle \rangle \,dt \\ &=\int_{t=a}^b \left( \frac{\del f}{\del x}\frac{dx}{dt}+\frac{\del f}{\del y}\frac{dy}{dt}+ \frac{\del f}{\del z}\frac{dz}{dt} \right)\,dt \endeq $$

But we recognize $(...)$ as $df/dt$ expanded with the chain rule, so we conclude that: $$\int_C\myv F\cdot d\myv r =\int_{t=a}^b \frac{d}{dt}f(t)\,dt=\left.f(t)\right|_a^b=f(\myv r(b))-f(\myv r(a)).$$

This is $\Delta f$, the change in "height" of the potential function between $\myv r(b)$ and $\myv r(a)$.

The integral only depends on the locations of the points at the beginning and end of the path.

At no point in what we just calculated did any details of the path $C$ come into play. So apparently...

The line integral of this conservative field, $\myv F$ is path independent.

In physics, the potential function often corresponds to a potential energy: Gravitational, electric potentials.

A potential function is like a well-behaved landscape. When a body moves in a conservative field, after a round trip, the body will return to the same position in the landscape, and thus it will have the same height (potential energy) as it started with.

In terms of the vector function $\myv F$...

A round trip--same starting and ending point--along a particular path is denoted as $\oint_C$. So we could also write this as $$\oint_C\myv F\cdot d\myv r = 0$$ for all round trips $C$.

Putting all of these together:

Conservative fields

Saved by a conservative field

Integrate the vector function $$\myv F = 2xy\uv i +x^2\uv j$$ along this fearsome-looking, 3-segment path:

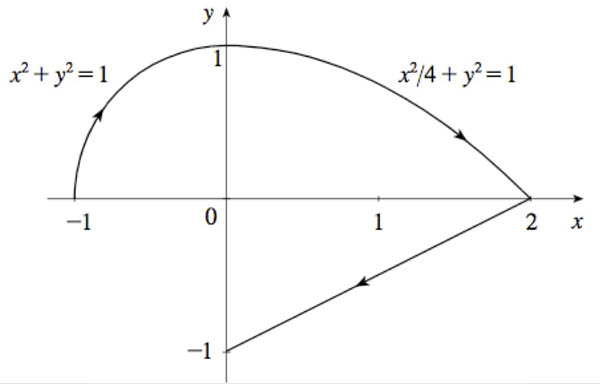
Could this $\myv F$ be the gradient of some function $f$? Applying our test$ \frac{\partial}{\partial y}P \stackrel{?}{=} \frac{\partial}{\partial x}Q$... $$ \frac{\partial}{\partial y}2xy=2x; \hspace{3em} \frac{\partial}{\partial x}x^2=2x;$$

Yes -- it's conservative! This opens up two simpler possibilities to evaluate the integral:

1. Guess the potential--After a little thought $f=x^2y$ should do the trick--and then just find the difference between the values of the potential at the end and beginning points: $$\int \myv F\cdot d\myv r=f(0,-1)-f(-1,0)=(0)^2(-1)-(-1)^2(0)=0.$$
2. Even if you can't guess the potential, you could still choose some *more convenient* path connecting the beginning and end points to integrate along, such as the straight line connecting $(-1,0)\to (0,-1)$.

To Do

• 06.3.think before you integrate

Visually

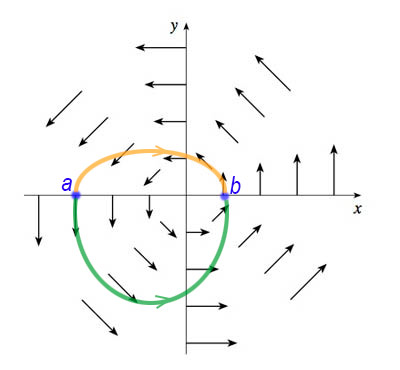Will the vector integral along the orange path be same as along the green path?

BTW - The vector integral $$\oint_C \myv F\cdot d\myv r$$ is also called a circulation integral. And a conservative field is also called "irrotational" because any circulation integral is zero.

Summary: path independence

For the vector field $\myv F=P\uv i+ Q\uv j$, the following statements are all equivalent and imply each other...

• Path independence $$\oint_{\text{all } C} \myv F=0$$
• The vector field is conservative.
• The vector field is irrotational. $$\myv \grad \times \myv F = 0$$
• Cross derivatives equal $$ \frac{\partial}{\partial y}P = \frac{\partial}{\partial x}Q $$
• The vector field is the gradient of some potential function $f$, $$\myv F=\myv \grad f.$$

Recipe to find the potential $f$ from a conservative $\myv F$

(Lab 06)

How to find the potential, $f$, instead of just guessing?

$\myv F=\myv \grad f$ implies that for any path connecting the origin with a point $(x,y)$ this integral will evaluate to $$\int_{(0,0)}^{(x,y)} \myv F\cdot d\myv r=\int \myv \grad f\cdot d\myv r= f(x,y)-f(0,0).$$ along *any* path. So, by integrating we'll find $f(x,y)$ to within a constant. But any constant (for example, $-f(0,0)$) can be added to $f$ and we'll still get the same $\myv F$ after taking the gradient.

Example

Consider the function $\myv F(x,y)= (\sin (x y)+x y \cos (x y))\uv i+ x^2 \cos (x y)\uv j$. Is it conservative?

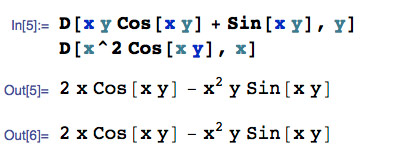
Yes!

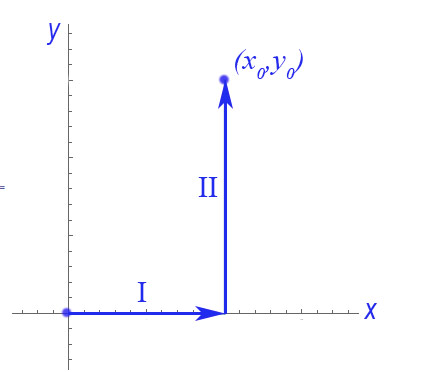Integrate $\myv F$ along this path from the origin to $(x_0,y_0)$.

(We're using $x_0$ and $y_0$ instead of $x$ and $y$ so as not to mix up the arguments of the functions being integrated and the integration limits. We'll go back and replace them at the end.)

Along path I: $y=0$ and d$\myv r = dx \uv i$ so $$\myv F \cdot d\myv r =\left.F_x\right|^{y=0}\,dx=(\sin(x\cdot 0)+x\cdot 0 \cos(x\cdot y))dx = 0$$ So the integral is $$\int_I\myv F \cdot d\myv r =\int_0^{x_0}0\,dx = 0.$$

Along path II: $x=x_0$ and d$\myv r = dy \uv j$ so $$\myv F\cdot d\myv r =\left.F_y\right|^{x=x_0}\,dy= x_0^2\cos(x_0 y) \,dy$$ So the integral is $$\int_{II}\myv F\cdot d\myv r = \int_0^{y_0}x_0^2\cos(x_0 y) \,dy= \left.x_0\sin(x_0y)\right|_0^{y=y_0}=x_0\sin(x_0y_0).$$

Adding and substituting $x_0\to x$ and $y_0\to y$: $$\int_I+\int_{II}=x\sin(xy)=f(x,y)-f(0,0).$$ And checking that the gradient of this function gives us our original vector function....

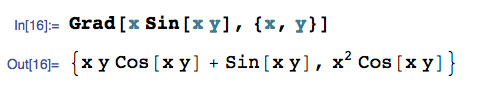
YUP!

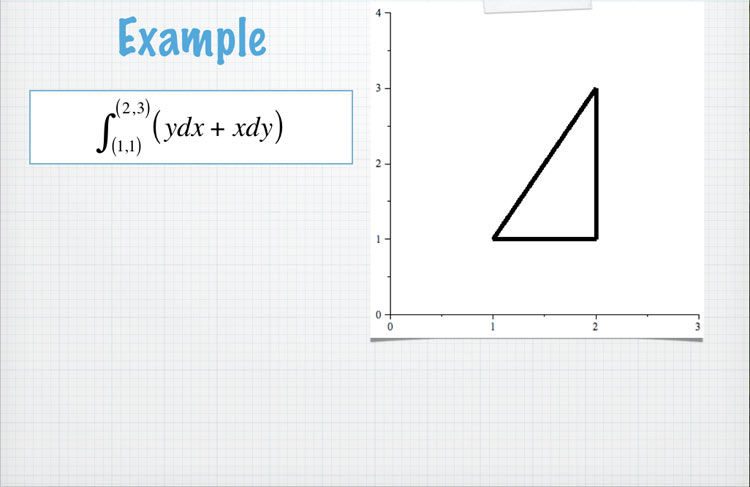
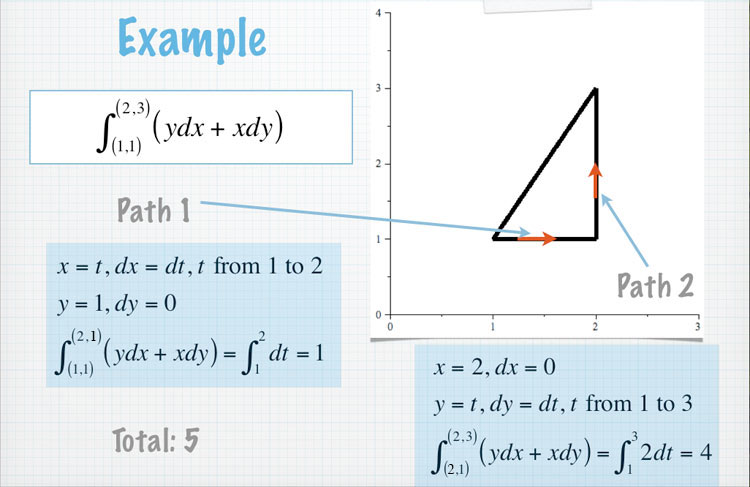
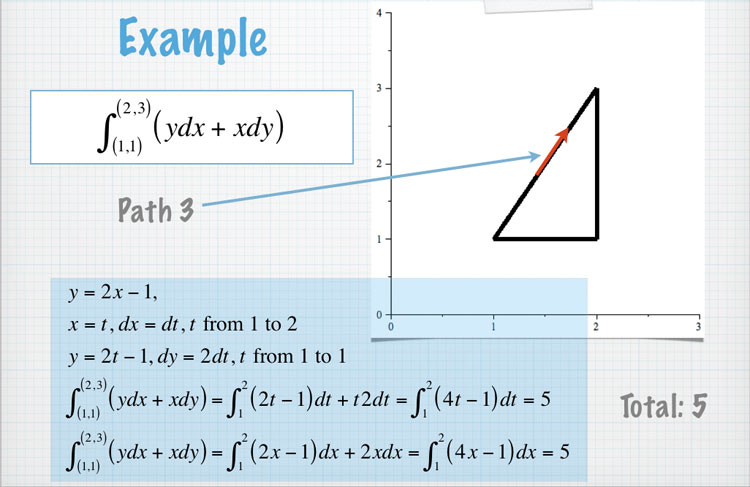
Checking a few paths

Let our potential function be... $$f(x,y)=xy$$

Then $f_x=y$ and $f_y=x$. So the vector function $$F=y\uv i +x\uv j$$ is conservative.

So, the integral... $$\int_C \myv F\cdot d\myv r=\int_{\myv r(a)}^{\myv r(b)}(y\,dx+x\,dy)$$ should be independent of the path $C$ taken.

Image credits

John Carrel`