Stokes' Theorem
Circulation!
Green's Theorem in terms of circulation integrals
Recapping Green's Theorem in terms of the tangential component of a vector field $F$ in the $xy$ plane:
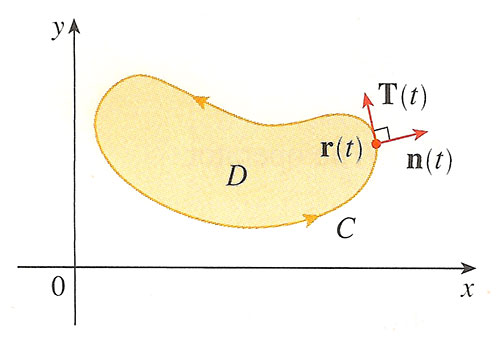
The left hand side of Green's theorem is the tangential component of $\myv F$ around $C$ (positive sense), that is, with $\myv F=P\uv i + Q\uv j$,
$$\oint P\,dx+Q\,dy=\oint \myv F\cdot d\myv r = \oint \myv F\cdot \uv T\,ds$$
The right-hand side of the Green's theorem $$r.h.s. = \iint_D\left(\frac{\del Q}{\del x}-\frac{\del P}{\del y}\right)\,dA$$ can be expressed in terms of a curl, if we treat $\myv F(x,y)$ as a three-dimensionsal field $\myv F(x,y,z)$ with a $z$-component of zero... $$\myv \grad \times \myv F=\text{det} \begincv \uv i &\uv j&\uv k \\ \frac{\del}{\del x} & \frac{\del}{\del y} & \frac{\del}{\del z}\\ P & Q & 0 \endcv = \left(\frac{\del Q}{\del x}-\frac{\del P}{\del y}\right)\uv k. $$ Green's theorem in terms of the curl of $\myv F$ was...
$$\oint_C \myv F\cdot \uv T\,ds = \iint_D \myv \grad \times \myv F \cdot \uv k\,dA. $$
This statement turns out to be a special case of Stokes' Theorem:
Stokes' Theorem Let $S$ be an oriented piecewise-smooth surface that is bounded by a simple, closed, piecewise-smooth boundary curve $C$ with positive orientation. Let $\myv F$ be a vector field whose components have continuous partial derivatives on an open region in $\mathbb{R}^3$ that contains $S$. Then $$\oint_C\myv F\cdot d\myv r=\iint_S \myv \grad \times \myv F \cdot d\myv S$$
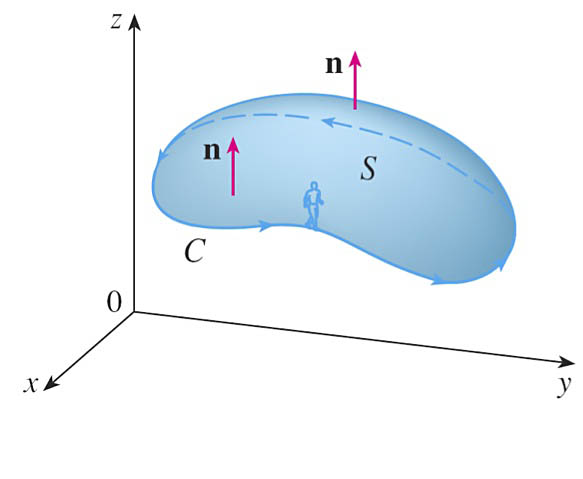
Since...
$$\oint_C \myv F\cdot d\myv r=\oint_C \myv F\cdot \uv T\,ds$$
and
$$\iint_S\myv \grad \times \myv F \cdot d\myv S=\iint_S\myv \grad \times \myv F\cdot \uv n \,dS,$$
the content of Stokes' theorem is that
- The integral of the curl ("circulation density") over a surface is equal to...
- the circulation around the boundary of the surface.
The surface in question can be *any* surface bounded by $C$!
Meaning of curl / circulation
Imagine that we zoom in on a surface in 3-d. If the surface is smoothly varying, and if $\myv F$ is a smoothly varying, continuous function, then perhaps it is plausible we can eventually zoom in sufficiently such that a small patch of the surface is very nearly flat.
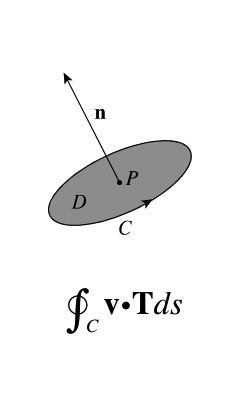Stokes' Theorem makes the claim that curl is a measure of circulation per unit area. If the vector field $\myv v$ is the velocity of fluid flow, then the circulation around a circle $C$ is the integral of the tangential component of $\myv v$ around the boundary of the circle.
Circulation is a measure of the extent to which $\myv v$ maintains the direction of the unit tangent $\uv T$ - the extent to which the flow is rotating in the direction of $C$.
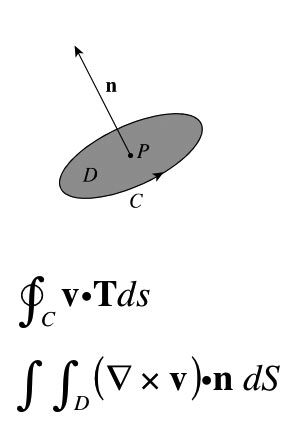Take a point $P$ within the flow and a disk $D$ with unit normal $\uv n$ surrounding $P$.
Stokes' theorem says that the circulation of $\myv v$ around $C$ is approximately equal to the average $\uv n$ component of $\myv \grad \times \myv v$ on $D$ multiplied by the area of $D$.
So the average $\uv n$ component of $\myv \grad \times \myv v$ on $D$ is equal to the circulation around $C$ divided by the area of $D$.
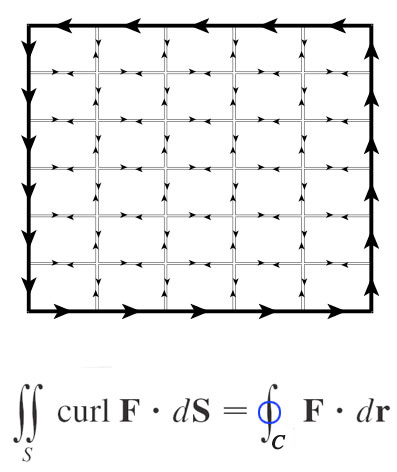
Integrating $\myv \grad \times \myv F$ for the region shown.
- Arrows show the circulation for each patch of surface $\Delta S$.
Inside the large rectangle the rotations cancel so the integration of curl F for the region is equivalent to integrating the flow along the boundary.
Example
Calculate the surface integral $\iint_S \myv \grad \times \myv F \cdot d\myv S$, where
- $\myv F(x,y,z)=6y\cos z\uv i +e^x\sin z\uv j+xe^y\uv k$
- $S$ is the half-sphere $x^2+y^2+z^2=49$ where $z\geq 0$, oriented upward.
Here's the half-sphere:
which is bounded by $C$, a circle of radius 7 centered at the origin.
The points on the circle are given by $$\myv r(t)=x(t)\uv i+y(t)\uv j+z(t)\uv k=7\cos t\uv i+7\sin t\uv j+ 0\uv k.$$ Traversing $C$ in the counterclockwise direction, $t$ runs from 0 to $2\pi$.
We can write $$\iint_S \myv \grad \times \myv F \cdot d\myv S= \oint_C\myv F\cdot d\myv r= \int_0^{2\pi}\myv F\cdot \myv r'(t)\,dt.$$ where the tangent vector is given by $\myv r'(t)=\langle x'(t),y'(t),z'(t)\rangle = \langle -7\sin t,7\cos t,0\rangle.$
Along $C$, $z=0$, and so $$\myv F(x,y,0)=\langle 6y\cos 0,e^x\sin 0,xe^y\rangle =\langle 6(7\sin t),0,7\cos t\, e^{7\sin t}\rangle.$$
The integral above becomes... $$\int_0^{2\pi}\myv F\cdot \myv r'(t)\,dt=\int_0^{2\pi}(42*-7*\sin^2 t+ 0+0)\,dt =-294\pi.$$
That circle in the x-y plane is also a boundary of the half-sphere below the x-y plane (the mirror image of the sphere pictured). If we move around the circle in the same way as above, Is the positive or negative *orientation* for the bottom half-sphere?
Based on your answer above, what is the value of the surface integral of the curl for the bottom half-sphere, with the normal vectors pointing outwards?
Therefore, What would the integral over the whole sphere be, with consistently "outwards" surface normal vectors?
Can you make a general statement about the surface integral of the curl for all closed surfaces?
First WebAssign question--"cube"...