Gradient, Divergence and Curl...as plumbing [6.5]
 Let's imagine the vectors $\myv F(\myv r)$ in a vector field in multiple dimensions as representing water flow. (Water is an approximately incompressible fluid.)
Let's imagine the vectors $\myv F(\myv r)$ in a vector field in multiple dimensions as representing water flow. (Water is an approximately incompressible fluid.)
- Gradient, $\myv \grad$: Which way does water flow in a landscape (=surface)?
- Curl, $\myv \grad \times$: Any swirling happening?
- Divergence, $\myv \grad \cdot$: Where are the leaks or faucets?
Gradient and the "nabla" _operator_
[The following ideas will be illustrated with functions of 2 variables, but can be extended to 3 or more variables.]
Consider a function which represents the height, $h(x,y)$, of a surface. The gradient of $h$:
$$\myv\grad h =h_x \uv i +h_y \uv j,$$
 points in the steepest "uphill" direction for the landscape $h$: If water is released at $(x,y)$ it should start flowing in the $-\myv \grad h$ direction.
points in the steepest "uphill" direction for the landscape $h$: If water is released at $(x,y)$ it should start flowing in the $-\myv \grad h$ direction.
Re-arranging how the gradient is written: $$\myv \grad h=\uv i \frac{\del}{\del x}h + \uv j \frac{\del}{\del y}h=\left[\uv i \frac{\del}{\del x} + \uv j \frac{\del}{\del y}\right] h,$$ suggests the idea of the *thing* in [...] "operating" on the scalar function, $h$, to produce the gradient vector field. This operator is called...
The nabla operator: $$\myv \grad \equiv \uv i \frac{\del}{\del x} + \uv j \frac{\del}{\del y}.$$
- It's a vector operator.
- When nabla operates on a scalar function, $h$, it produces a vector field: the gradient field. $$\myv \grad h(x,y) = \frac{\del h}{\del x}\,\uv i+\frac{\del h}{\del y}\,\uv j.$$
The Curl
The cross-product-like object involving $\myv \grad$ and a vector field $\myv F=P(x,y,z)\uv i+Q(x,y,z)\uv j + R(x,y,z)\uv k$ is
The curl of a vector field $\myv F$ is: $$\begineq\myv \grad \times \myv F &= \begincv \uv{i}& \uv{j}& \uv{k}\\ \frac{\del}{\del x} & \frac{\del}{\del y} & \frac{\del}{\del z}\\ P& Q& R\endcv \\ &= \uv{i}\left(\frac{\del R}{\del y}-\frac{\del Q}{\del z}\right) + \uv{j}\left(\frac{\del P}{\del z}-\frac{\del R}{\del x}\right) +\uv{k}\left(\frac{\del Q}{\del x}-\frac{\del P}{\del y}\right)\endeq.$$
If $\myv F$ is a function of only $x$ and $y$, then only the $\uv k$ component is non-zero.
For $\myv F(\myv r) = -y \uv{i} +x \uv{j}$, sketch $\myv F$ in the $x-$, $y-$ plane ($z=0$)...
 $$\myv \grad \times \myv F = \begincv \uv{i}& \uv{j}& \uv{k}\\
\frac{\del}{\del x}&\frac{\del}{\del y}&\frac{\del}{\del
z}\\
-y& +x& 0\endcv = 2\uv{z}.$$
$$\myv \grad \times \myv F = \begincv \uv{i}& \uv{j}& \uv{k}\\
\frac{\del}{\del x}&\frac{\del}{\del y}&\frac{\del}{\del
z}\\
-y& +x& 0\endcv = 2\uv{z}.$$
For this function, notice that the curl has the same value everywhere, not just at the origin.
"Swirliness" defined by a paddle-wheel
Again thinking of $\myv F$ as the field specifying water velocity...
Imagine placing a  paddle-wheel
with axis oriented in the $\uv{k}$ direction in the water flow represented
by the vector function $\myv F$ and seeing whether it turns counter-clockwise
(positive curl) or clockwise (negative curl).
paddle-wheel
with axis oriented in the $\uv{k}$ direction in the water flow represented
by the vector function $\myv F$ and seeing whether it turns counter-clockwise
(positive curl) or clockwise (negative curl).

In a 3-d water flow field, we could also try orienting the paddle wheel towards $\uv{j}$ or $\uv{k}$ to check for components of the curl in all possible directions.
Conservative fields and curl
We saw that fluid flow in a landscape is related to the gradient field.
Can you imagine some kind of landscape/surface that would give rise to this flow?

Howzabout this landscape?...

Or this somewhat more realistic one?...

Theorem 3 says...
If $f$ is a function of 3 variables, that has continuous second-order partial derivatives, then $$\myv \grad \times (\myv \grad f) = 0$$ at all points $(x,y,z)$.
Alternative statements:
- Any swirliness in the flow $\myv F$? Sorry, there's no landscape for which $\myv F$ represents the flow. (There's no potential function, $h$.)
- A vector field $\myv F$ is conservative if, and only if, $\myv \grad\times \myv F=0$.
This is a test we can use on any vector field $\myv F$ to decide whether it's worth looking for a potential function or not!
A field $\myv F$ is said to be irrotational if for all points in space: $$\myv \grad \times \myv F=0$$
The Divergence
We could form a dot product between the nabla vector operator and...
a vector field, $\myv F(x,y)=P(x,y)\uv i +Q(x,y)\uv j$, where $P$ is the $x$-component of $\myv F$.
The dot product of two vectors is a scalar. This defines...
The divergence of $\myv F(x,y)$ is $$\begineq \myv \grad \cdot \myv F &= \left(\uv{i} \frac{\del}{\del x} +\uv{j} \frac{\del}{\del y}\right) \cdot \left( P\uv{i} + Q\uv{j}\right)\\ &=\frac{\del P}{\del x} + \frac{\del Q}{\del y}.\endeq$$
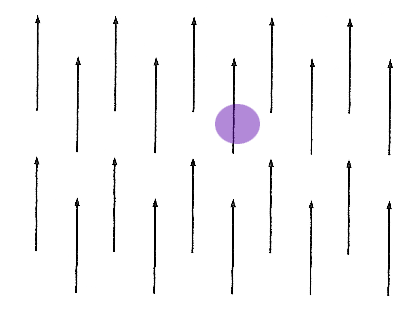
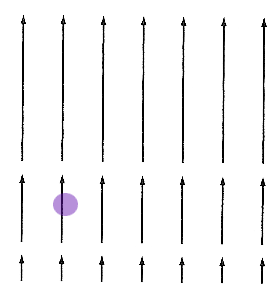
For the following sketches of 2-dimensional vector fields, $\myv F(x,y)$, what [pos, neg or 0] is the 2-d divergence, $\frac{\del P}{\del x}+\frac{\del Q}{\del y}$ at the positions marked in purple?
$\myv F(x,y)=3\, \uv j$
$\myv F(x,y)=x\uv i +y\uv j$

You can estimate visually, without a formula... For the vector field above:
Estimating the divergence of a vector field - Narrated: 2 min.

Where are the leaks (or faucets)?
Imagine that the arrows, $\myv F(x,y)$, represent the velocity of 2-d flow of an incompressible fluid (water!).
Now imagine injecting a "cloud" of purple dye at a location you'd like to investigate for "leaks" in your system, places where the water is disappearing.
A place where the cloud gets smaller corresponds to a location where the divergence is negative: a "leak" (or sink, or drain) where water is leaving your 2-d system

...leaving your 2d system **into another dimension**!
Places where the cloud gets bigger have positive
divergence. There must be a "source" (or faucet) of water **from another dimension**(!).

Consider again these vector fields, as if $\myv F$ of water flow... What's happening to the size of the purple spot?



Incompressible fields
Incompressible means $$\myv \grad \cdot \myv F = 0.$$
When the fluid flow is incompressible, then, if the vectors represent water flow, just as much water enters any bounded volume as exits the volume.
$\myv F(x,y)=3\, \uv j$

$\myv F(x,y)=x\uv i +y\uv j$

Electric fields The divergence of the electric field is zero, except where there are charges, $\myv \grad \cdot \myv E(x,y,z) \propto \rho(x,y,z)$, where $\rho$ is the charge density. This statement is equivalent to saying: Charges are the sources or sinks of the electric field.
- MathInsight.org: the divergence idea.
In the /mvhandouts/ folder... 06.5.VisualDivCurl.php