Stokes' and Divergence Theorems
Parametric surfaces
In the topic on parametric surfaces [12.5] we saw how to express a surface in terms of two parameters $u$ and $v$. The surface is specified by
$$\myv r=x(u,v)\uv i+y(u,v)\uv j+z(u,v)\uv k$$
The surface area is $$A_S=\iint_S 1\,dS = \iint_D\left|\myv r_u \times \myv r_v \right|\,dA.$$
The surface integral
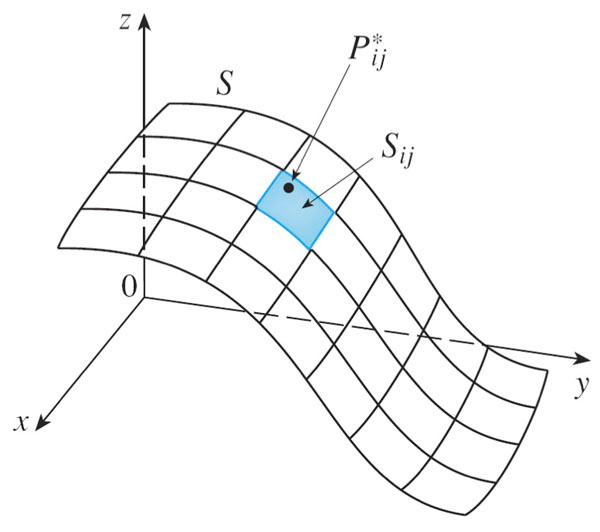
Defining the surface integral in terms of the Riemann sum
Definition
General definition in the parameter space $u$, $v$: $$\iint_S f(x,y,z)\,dS= \iint_D f(\myv r(u,v)) \left|\myv r_u \times \myv r_v \right|\,du\,dv.$$
With $z=g(x,y)$, if we take the parameters to be $x$ and $y$ this turns into $$\iint_S f(x,y,z)\,dS= \iint_D f(x,y,g(x,y))\sqrt{1 + \left(\frac{\del g}{\del x}\right)^2 +\left(\frac{\del g}{\del y}\right)^2 }\,dx\,dy.$$
Oriented surface
We'll shortly be integrating normal components of vector fields.
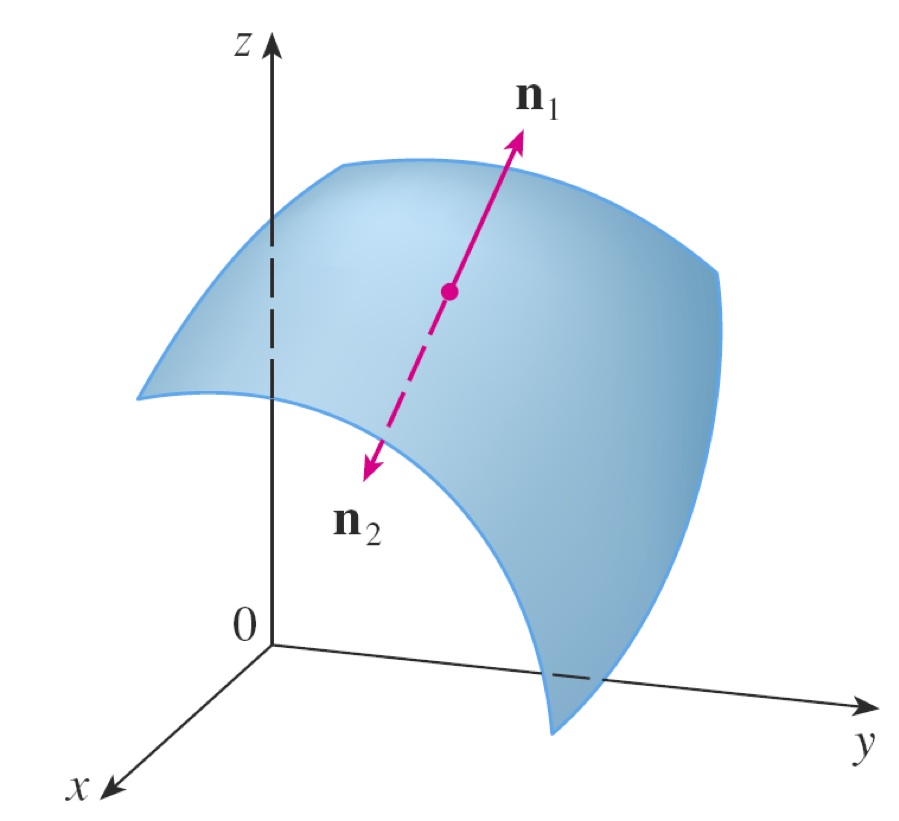There are two possible surface normal orientations.
For closed surfaces we can define a convention for which surface normal to choose.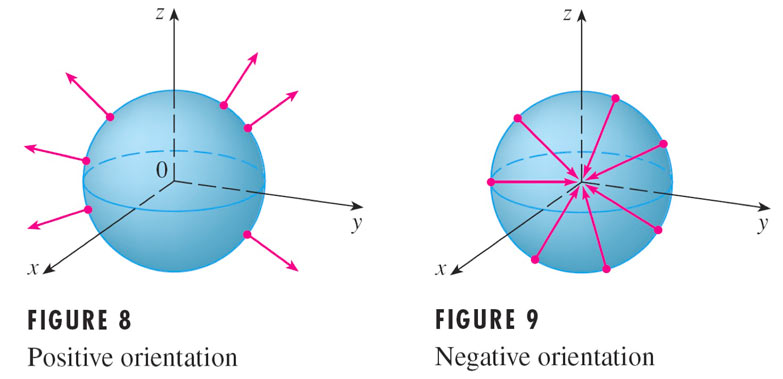
Surface, or flux integral
If necessary, we will use a simpler convention that the positive normal direction is up.
The flux integral or the surface integral of a vector field is $$\iint_S\myv F\cdot \uv n \,dS$$
In terms of the parameters $u$ and $v$,
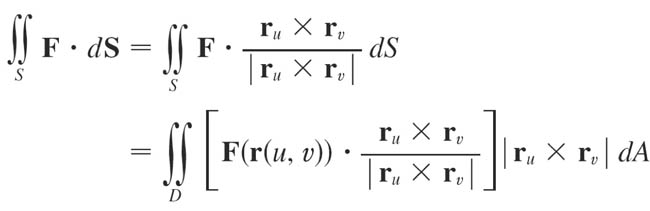
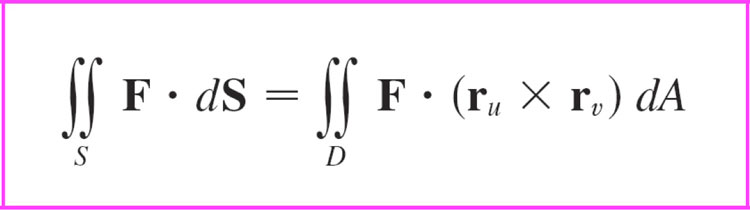
Vector forms of Green's Theorem
Here again are the vector forms of Green's Theorem: $$\oint_C \myv F\cdot \uv T\,ds = \iint_D \myv \grad \times \myv F \cdot \uv k\,dA. $$ $$\oint_C \myv F\cdot \uv n\,ds = \iint_D \myv \grad \cdot \myv F \,dA. $$
Stokes' Theorem
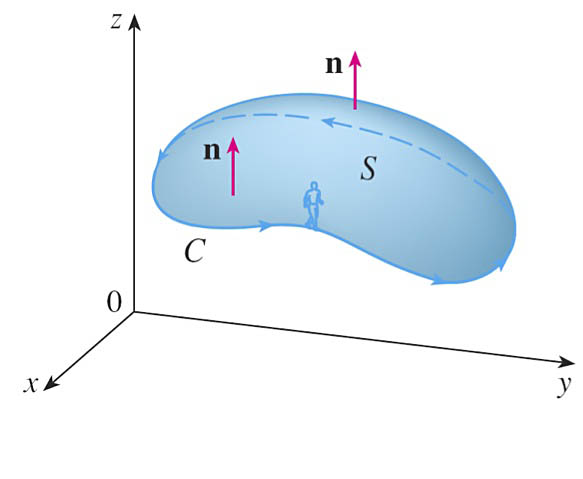
Since... $$\oint_C \myv F\cdot d\myv r=\oint_C \myv F\cdot \uv T\,ds$$ and $$\iint_S\myv \grad \times \myv F \cdot d\myv S=\iint_S\myv \grad \times \myv F\cdot \uv n \,dS,$$ the content of Stokes' theorem is that
- The integral of the circulation density over a surface is equal to
- the circulation around the boundary of the surface.
Meaning of curl / circulation
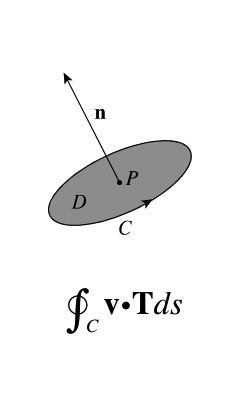Curl is a measure of circulation per unit area. If the vector field $\myv v$ is the velocity of fluid flow, then the circulation around a circle $C$ is the integral of the tangential component of $\myv v$ around the boundary of the circle.
Circulation is a measure of the extent to which $\myv v$ maintains the direction of the unit tangent $\uv T$ - the extent to which the flow is rotating in the direction of $C$.
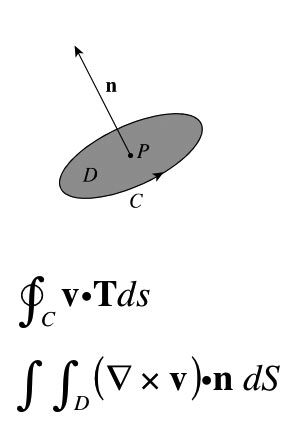Take a point $P$ within the flow and a disk $D$ with unit normal $\uv n$ surrounding $P$.
Stokes' theorem says that the circulation of $\myv v$ around $C$ is approximately equal to the average $\uv n$ component of $\myv \grad \times \myv v$ on $D$ multiplied by the area of $D$.
So the average $\uv n$ component of $\myv \grad \times \myv v$ on $D$ is equal to the circulation around $C$ divided by the area of $D$.
Integrating $\myv \grad \times \myv F$ for the region shown.
- Arrows show the circulation for each patch of surface $\Delta S$.
Inside the large rectangle the rotations cancel so the integration of curl F for the region is equivalent to integrating the flow along the boundary.
The Divergence Theorem
Compare to this vector version of Green's theorem: $$\oint_C \myv F\cdot \uv n\,ds = \iint_D \myv \grad \cdot \myv F \,dA. $$
The divergence at a point is something like the local 'flux density'.
The integral of the flux density over a solid region is equal to the flux through the surface boundary of the region.
Example
Calculate the flux through just the surface
$\iint_S \myv F\cdot \uv n \,dS$
where $S$ is the surface with vertices $(9,0,0)$, $(0,9,0)$, $(0,0,9)$,
and the vector field is
$$\myv F(x,y,z)=(x+y^2)\uv i+(y+z^2)\uv j+(z+x^2)\uv k$$
I'll use this form of the surface integral: $$\iint_S f(x,y,z)\,dS= \iint_D f(x,y,g(x,y))\sqrt{1 + \left(\frac{\del g}{\del x}\right)^2 +\left(\frac{\del g}{\del y}\right)^2 }\,dx\,dy.$$
The equation of the plane containing the triangle is.. $$x+y+z=9 \Rightarrow z=g(x,y)=9-x-y$$
- $g_x=g_y=-1$ so the square root factor is $\sqrt{3}$
- the limits of integration are $$\iint_D=\int_{x=0}^9\int_{y=0}^{9-x}$$
The function $f(x,y,z)=f(x,y,g(x,y))$ in the integral is $\myv F\cdot\uv n$.
- The unit normal vector to the plane is $\uv n=\frac{1}{\sqrt 3}\langle 1,1,1\rangle$,
- so $$\myv F\cdot \uv n = \frac{1}{\sqrt 3} \left(x+y^2+y+z^2+z+x^2\right)$$
- substituting in $z=9-x-y$ on the triangular surface, Mathematica expands this to... $$\myv F\cdot\uv n = \frac{1}{\sqrt 3}(90 - 18 x + 2 x^2 - 18 y + 2 x y + 2 y^2)$$
Putting this all together... $$\iint_D\myv F\cdot \uv n dS = \int_{x=0}^9\int_{y=0}^{9-x}(90 - 18 x + 2 x^2 - 18 y + 2 x y + 2 y^2)\,dy\,dx.$$
Example
Calculate the total flux through *all* the surfaces of the volume bounded byt the triangle, and the planes $x=0$, $y=0$, $z=0$.
with
$\iint_S \myv F\cdot \uv n \,dS$
where
$$\myv F(x,y,z)=(x+y^2)\uv i+(y+z^2)\uv j+(z+x^2)\uv k=P\uv i+Q\uv j+R\uv k.$$
This turns out to be significantly easier! We'll calculate it from the right side of the divergence theorem:
∯${}_S \myv F \cdot \uv n dS = \iiint_E \myv \grad \cdot \myv F dV.$
The divergence is $$\myv \grad \cdot \myv F =\frac{\del P}{\del x}+\frac{\del Q}{\del y} +\frac{\del R}{\del z}= 1+1+1=3.$$
So, $$\iiint_E \myv \grad \cdot \myv F dV=3\iiint_E\,dV=3*(9*9*9/3)=729.$$
Example
∯${}_S \myv F \cdot \uv n dS = \iiint_E \myv \grad \cdot \myv F dV.$
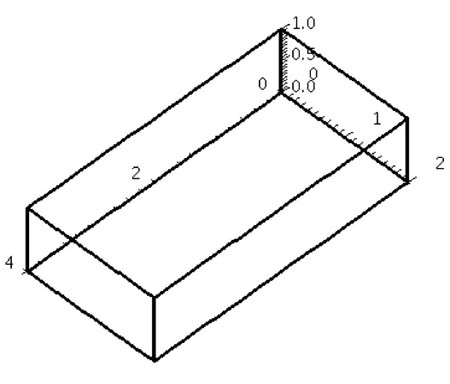For some function $\myv F=P\uv x+Q\uv y+R\uv j$...
[Normal vectors?]