Chapter 9

Learning objectives

Distance formula

The 2d Pythagoras' theorem is the distance between two points $P=(x_1,y_1)$ and $Q=(x_2,y_2)$.

Defining the differences $\Delta x \equiv x_2-x_1$ and $\Delta y \equiv y_2-y_1$, the length of the hypotenuse of a right triangle representing the distance is related to the point coordinates by: $$h^2 = (\Delta x)^2 + (\Delta y)^2$$

In 3-dimensions, $P=(x_1,y_1,z_1)$ and $Q=(x_2,y_2,z_2)$. The Py"three-d"agoras' theorem gives the distance between the points as: $$h^2 = (\Delta x)^2 + (\Delta y)^2 +(\Delta z)^2.$$

Vectors

Vector addition / subtraction / scalar multiple: Geometrically (visually) and in terms of vector components.

Two vectors are parallel if $\myv a=k\myv b$. Perpendicular if $\myv a \cdot \myv b=0$.

Visualizing surfaces: traces and contours

The intersection of the plane $x=k$ with a surface in 3 dimensions is a curve called an $x=k$ trace. If the surface can be expressed in terms of a function $f(x,y)=z$, then an equation for the trace is $z=f(k,y)$.

Be able to calculate and use $x=k$ traces, $y=k$ traces, and $z=k$ traces (or contours) to envision a surface in 3 dimensions. -AND- be able to go from a 3-d depiction of a surface to some likely traces.

Vectors: Dot product understandings

$\cos \theta$: "How parallel" are two vectors?
Product of length of two vectors $\times$ "how parallel"? $$\myv a \cdot \myv b = ab\cos\theta.$$
a scalar number.
Know how to calculate from Cartesian components $$\myv a\cdot \myv b = a_xb_x +a_yb_y+a_zb_z.$$ And the norm or length of a vector, written as $|\myv a| \equiv a$, obeys: $$\myv a\cdot \myv a =a^2=a_x^2 +a_y^2+a_z^2.$$

Vectors: Cross product understandings

$\sin\theta$: "How perpendicular" are two vectors?
Product of length of two vectors $\times$ "how perpendicular" $$\myv a \times \myv b = ab\sin\theta \uv n$$
a vector pointing in the $\uv n$ direction (given by right-hand-rule).
Know how to calculate manually from components.
Interpretation as the area of a parallelagram defined by $\myv a$ and $\myv b$.

$$\myv a \times \myv b \cdot \myv c$$ is the volume of the parallelipiped define by $\myv a$, $\myv b$, and $\myv c$.

Lines

Two vectors, $\myv a$ and $\myv b$, are parallel if one is a non-zero, scalar multiple of the other: $$\myv a =k\myv b$$

The parametric equation for a line: $$\myv r(t)=\myv r_0+t\myv v$$

A line parallel to a direction vector $\myv v$,
passing through a point specified by the position vector, $\myv r_0$, a vector in standard position (with its tail at the origin).
You can find the line through two points, $P=(p_1,p_2,p_3)$ and $Q=(q_1, q_2, q_3)$ by calculating the difference vector $\myvv{PQ} = \langle q_1-p_1, q_2-p_2, q_3-p_3\rangle$. $\myv r_0$ can be either of the position vectors $\myv P$ or $\myv Q$, and the direction vector of the line can be any scalar multiple of $\myvv{PQ}$.

Planes

A plane can be determined by

a point $P_0$ in the plane and
a normal vector, $\myv n$, which is orthogonal (normal) to the plane.

In pictures...

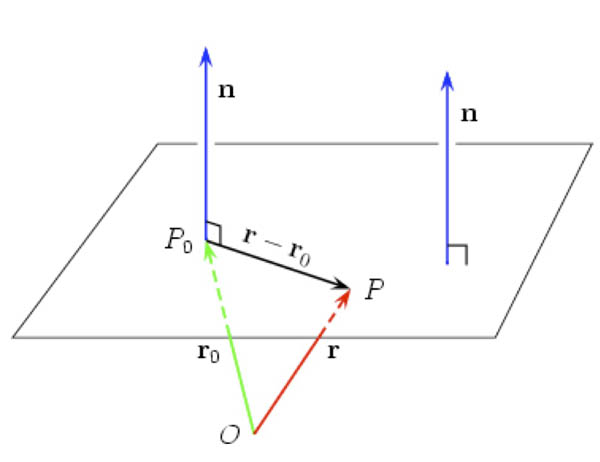
$\myv r_0=\langle x_0, y_0, z_0 \rangle$ is a vector pointing at $P_0$.
$\myv n = \langle\color{blue}a, b, c\color{black} \rangle$ is the normal vector.
$\myv r=\langle x,y,z\rangle$: Some point in the plane, which must satisfy the condition that $\myv r -\myv r_0$ is perpendicular to $\myv n$:

With these definitions:

Equations of a plane: $$\begineq \text{"vector" eq:}\ \ \ \ 0&=\myv n \cdot (\myv r-\myv r_0)\\ &=\langle \color{blue}a,b,c\color{black} \rangle \cdot \langle x-x_0,y-y_0,z-z_0\rangle\\ \text{"scalar" eq:}\ \ \ \ 0&=\color{blue}a\color{black} (x-x_0)+\color{blue}b\color{black}(y-y_0)+\color{blue}c\color{black}(z-z_0)\rangle\\ \endeq $$

Derivatives and Integrals of vector functions

A vector-valued function is a function whose output is a vector, $\myv r$, (usually a position vector) with components that are functions of a single parameter, e.g. $$\myv r(t)=\langle x(t), y(t), z(t)\rangle.$$ Such a function can trace out a path / curve / trajectory in space.

The derivative of such a function is: $$\myv r'(t)\equiv \frac{d\myv r(t)}{dt}=\langle x'(t), y'(t), z'(t) \rangle.$$ The derivative is a vector which points in a direction tangent to the curve at $\myv r(t)$

Think of $\myv r(t)$ as the position of a particle moving in space, as a (parametric) function of time $t$. The particle follows a trajectory, a curve or path in space parameterized by the variable $t$. Then we can interpret the derivatives of this function:

$\myv r'(t)\equiv\myv v(t)$ is the instantaneous velocity vector
$\myv r'(t)$ points in a direction tangent to the path of the particle.
The magnitude of the velocity vector, $|\myv r'(t)|\equiv |\myv v(t)| \equiv v(t)$ is the speed of the moving particle.
$\myv r''(t)\equiv \myv a(t)$ is the acceleration vector of the particle.

Path length & Curvature

As a particle traverse a path $P$, parameterized as $\myv r(t)=\langle f(t), g(t), h(t)\rangle$ it traces out a path in space. $s(t)$ represents the "arc length", or distance along the path, which the particle travels between some initial time (often represented as "0") and some final time (often represented as "t"). Since distance = speed * time, the arc length function is the integral of $ds=v\,dt$: $$ s(t) = \int_0^t v\,dt= \int_0^t \sqrt{\left(\frac{d f(t)}{d t}\right)^2 +\left(\frac{d g(t)}{d t}\right)^2 +\left(\frac{d h(t)}{d t}\right)^2 }\,dt.$$ Along the curve, the rate of the change of the arclength function with respect to the parameter $t$ (time) is the same as the speed if the vector function tracing out the path: $$\frac{ds}{dt}=\left|\frac{d\myv r}{dt}\right|=\left|\myv r'(t)\right|.$$ The unit tangent vector is $$\uv T = \frac{\myv r'}{|\myv r'|},$$ and the curvature, $\kappa$ is defined to be: $$\kappa = \frac{d\uv T}{ds}= \frac{|\uv T'(t)|}{|\myv r'(t)|} .$$ The curvature of a circle of radius $a$ is $\kappa=1/a$. So we can draw an "osculating circle" of radius $a=1/\kappa$ on the inside of any curve, at a point $P$ on a curve where the curvature is $\kappa$, and the circle will nestle nicely tangent to the curve at that point.

There is an associated "normal vector", $\uv N$, $$\uv N(t) \equiv \frac {\uv T'(t)}{|\uv T'(t)|}.$$ which is perpendicular to the curve at point $P$, and points towards the center of the osculating circle at $P$.