3-dimensional coordinate systems [9.1]

Locating objects in 3-dimensions
In single-variable calculus, you can visualize the graph of a function by graphing $y\equiv f(x)$ vs $x$.
We will visualize functions of 2 variables by graphing $z\equiv f(x,y)$ vs $x$ and $y$.
You will become familiar with
- points in 3-d,
- curves and lines in 3-d, which can be represented by 2-d visualizations on screens and pages, equations, vector functions of 2 or more variables and parametric vector functions of one independent variable.
- planes and surfaces, which can often be represented by 2-d visualizations, vector functions and parametric functions of 2 independent variables.
Calculus I and II were largely concerned with functions of one variable...
A function of one variable is a rule that assigns exactly one real number (output) to each input real number.
But we are interested in this course in functions that depend on more than one variable.
A function of $n$ variables is a rule that assigns exactly one real number (output) to each input ordered [pair / 3-tuple / 4-tuple .../ $n$-tuple] of real numbers.
Come up with an example of some quantity (function) that depends on 2 or more independent variables.
Schlicker, 9.1 exercises
7,*10*, 11a, 12ab
We will want to visualize / graph / differentiate / integrate these functions. Sometimes it is straightforward to generalize what we did in single-variable calculus to multi-variable calculus. Sometimes there are new challenges and new concepts that were not needed in single-variable functions.
Today:
- Right-handed Cartesian coordinate systems
- Points in 3-D space
- Equations of planes
- Distance formula in 3 dimensions
- Equations of spheres
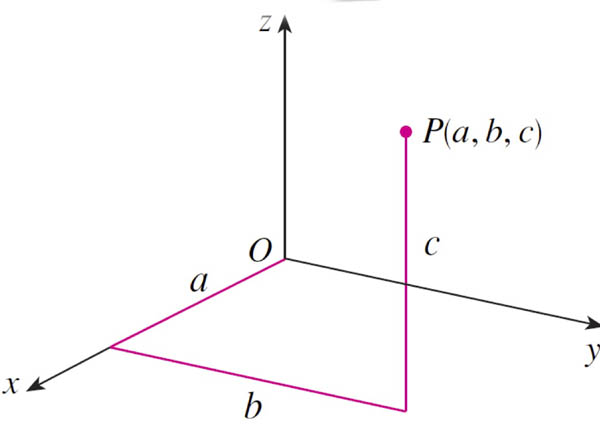
Rectangular coordinates
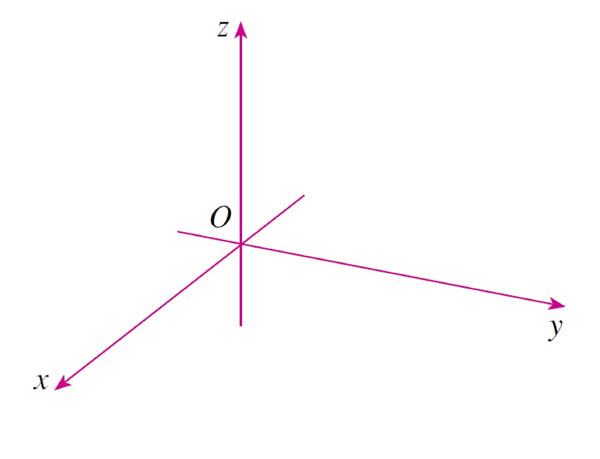
Also known as Cartesian coordinates, after Renes Descartes.
- The three coordinate axes are mutually orthogonal, that is, at right angles to each other.
- The letters $x$, $y$, and $z$ are placed on the parts of each of the coordinate axes which are positive
Does it matter how we arrange the positive $x$, $y$, and $z$ axes?

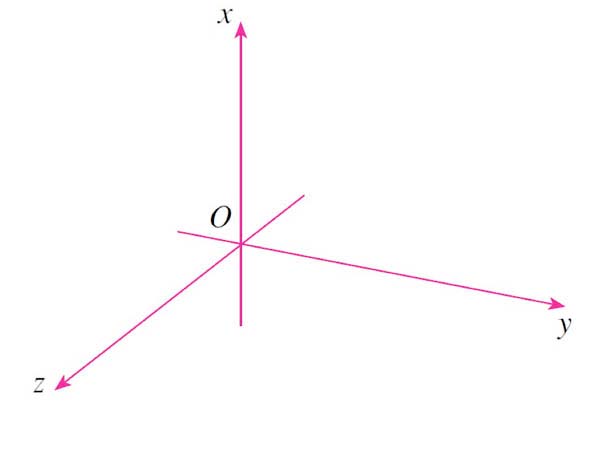
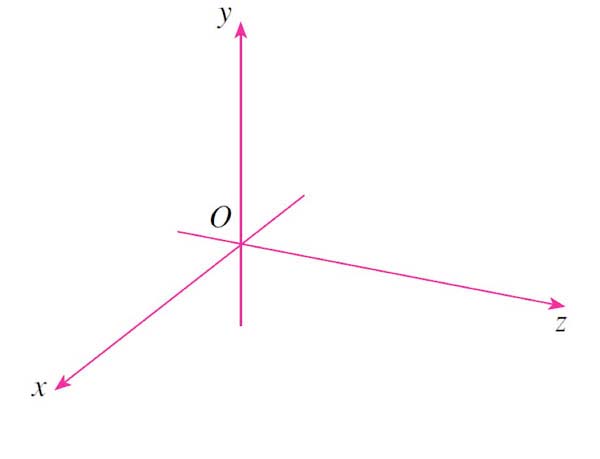
 of the arrangements have the property that one can be *rotated* in space to arrive at the other arrangement. The other one can not be rotated into either of the other two arrangements. Which is the odd one out?
of the arrangements have the property that one can be *rotated* in space to arrive at the other arrangement. The other one can not be rotated into either of the other two arrangements. Which is the odd one out?It may help to hold three fingers of your hand at right angles, like this picture on the Swiss 200 Franc banknote. Write 'x', 'y', and 'z' on your thumb, index, and middle finger and then move them around! For some of the orientations above you can match up with your right hand (as pictured on the bill). For some of the orientations you may have to use your left hand instead.
We say that the two above that can be rotated into each other (with the same hand) have the same 'relative orientation'.
If you were to consider all possible permutations of $x$, $y$, and $z$ on the six different directions in the picture, you would find that there are only two possible relative orientations. One is the right-hand orientation pictured, and the other is with the left hand.
Does it matter which one we pick?
Yes:
When we get to writing the cross product $\myv a \times \myv b$ in terms of the Cartesian components of $\myv a$ and $\myv b$ the formula for the product in one system will give us a vector which is exactly -1 times the product in the other system.
So which one to pick? Like driving on the right or the left, either one would be OK. But it's simpler and safer if everyone agrees to do the same thing!

Sweden changed from driving on the left to driving on right, 5 AM, September 3, 1967.
Right-handed coordinate system
Another way, besides carrying around a 200 franc not:
- Take your right hand...
- Point your straight fingers in the positive $\hat x$ direction.
- Rotate your hand so that you can curl your fingers* to point in the positive $\hat y$ direction.
- Your thumb now points in the $\hat z$ direction.
* You need to be able to curl your fingers through an angle less than $180^o$.
Try x and y, then x and z and y and z, and figure out which way the other axis points.
To Do
Go to GeoGebra.org/3d. The blue axis is the $z$ axis. Using your right hand, figure out and identify by color which of the other two axes is $x$ and which one is $y$.
...did I ask you to figure this out?
Your brain and eyes work together to easily (unconsciously) make sense of the 3-d world around you. It is terrifically useful to take advantage of this system to imagine relations in 3-d space. But the 2-d pictures on a textbook page or a computer screen can only suggest 3-d reality. Visualization is a skill worth developing, to look at such a picture and be able to imagine it in 3-d.
Coordinates
Coordinate planes
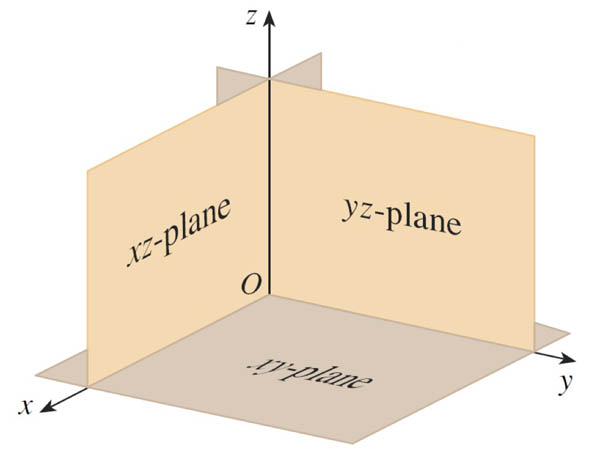
- Any point with an $x$-coordinate of zero is in the $yz$ plane.
- $y=0$ $\Rightarrow$ A point is in the $xz$ plane.
- $z=0$ $\Rightarrow$ A point is in the $xy$ plane.
Geogebra
All of these graph the same set of points. The set of points forms a surface in 3 dimensions:
- formulas for $(x,y,z)$:
(x, y, x^2+y^2): Graphs all the points that have x-coordinate=$x$, y-coordinate=$y$, and z-coordinate=$x^2+y^2$. - function definition:
f(x,y) = x^2+y^2: Graphs all the points with coordinates $(x,y,f(x,y)$. That is, $f(x,y)\equiv z$. - an equation:
x^2+y^2-z = 0orz = x^2+y^2: The surface consists of the points that satisfy the equation that you've typed in.
Projections
...of points
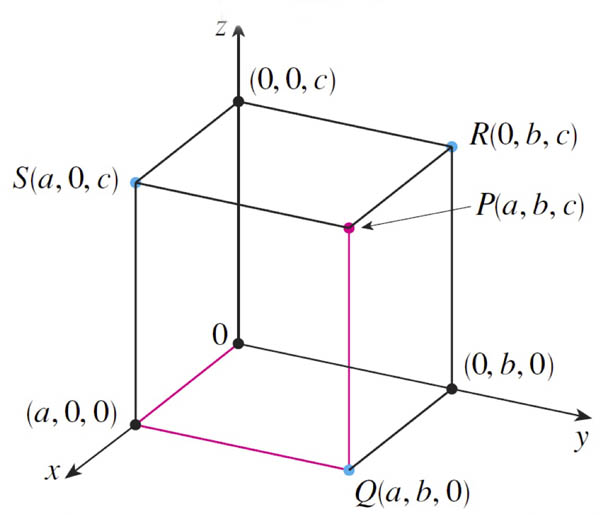
$S=(a,0,c)$ is the projection of $P$ onto the $xz$ plane. All of these are equivalent ways to find this projection:
- Find the closest point to $P$ on the $xz$ plane. -OR-
- Imagine a line from $P$ to the $xz$ plane that is perpendicular to the plane. The intersection of that line with the $xz$ plane is $S$. -OR-
- Imagine a star that is so far away along the $y$ axis that its light rays appear to be mutually parallel, and all hitting the $xz$ plane at a right angle. $S$ is the shadow of point $P$ on the $xz$ plane.
$(0,b,0)$ is the projection of $P$ onto the $y$-axis. These two of the above ways of thinking work for this projection:
- Find the closest point to $P$ on the $y$ axis. -OR-
- Imagine a line from $P$ to the $y$ axis that is perpendicular to the $y$ axis. The intersection of that line with the $y$ axis is our projection.
The space $\mathbb{R}^3$
$\mathbb{R}\equiv$ the real numbers.
- Cartesian Product:
$\mathbb{R}^3\equiv \mathbb{R}\times\mathbb{R}\times\mathbb{R}=\{(x,y,z) | x,y,z\in \mathbb{R}\}$. - Set of all ordered triples.
Surfaces in $\mathbb{R}^3$
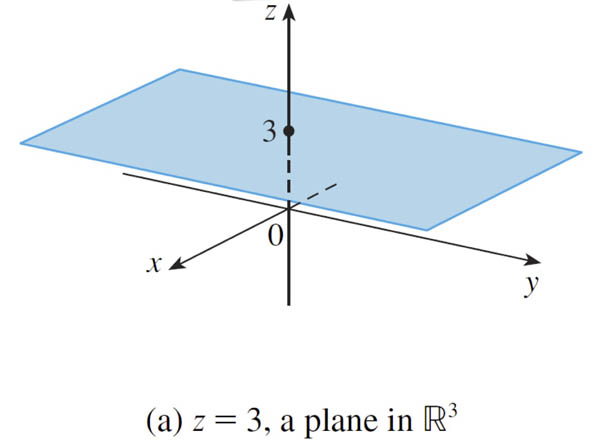
All points with coordinates $(a,b,c)$ where $c=3$
[and $a$ and $b$ can be anything]
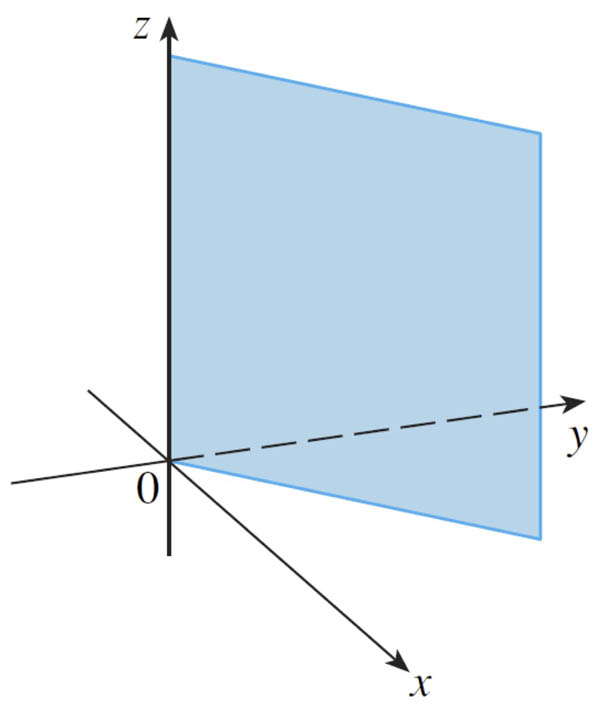
All points with coordinates $(x,y,z)$ where $y=x$.
Notice that $y=x$ is the definition of a line in 2-d with a slope of 1. But here??
Anything a bit deceptive about the picture above?
Should continue to values with x and y less than 0...
To Do
- Section 9.1 Group Work: Fun with Visualization [missing]
- Working with surfaces in 3D space [missing]
Distance
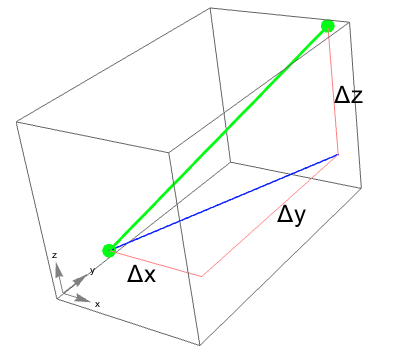
What is the distance $|P_1P_2|$ between two points $P_1(x_1,y_1,z_1)$ and $P_2(x_2,y_2,z_2)$ in three dimensional space?
- The blue line is the hypotenuse of the triangle with legs $\Delta x$ and $\Delta y$: It's length is $\sqrt{(\Delta x)^2+(\Delta y)^2}$.
- The green line is our distance, and is the hypotenuse of the right triangle with legs of $\Delta z$ and the blue line.
So, our distance formula is: show / hide
$$|P_1P_2|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}.$$
Equation of a sphere
All the points on a sphere are the same distance, $r$, away from its center, $C(h,k,l)$. Using the distance formula: $$(x-h)^2+(y-k)^2+(z-l)^2 = r^2.$$
For any of the equations below: The set of points,$\{(x,y,z)\}$ that satisfies the equation forms a surface in 3 dimensions. For each equation, make a guess at the surface corresponding to the equation, then check it by typing the equation into GeoGebra: [Hint, think about what the distance formula implies.]
- $$ 9=x^2+y^2+z^2.$$
- $$z=\sqrt{ 9-x^2-y^2}.$$
- $$9=x^2+y^2.$$
Problem 9.1.038
Consider a 2-d variation of this problem...Find all the points, $P$, (they form a circle) that are twice as far from $A$ as they are from $B$.
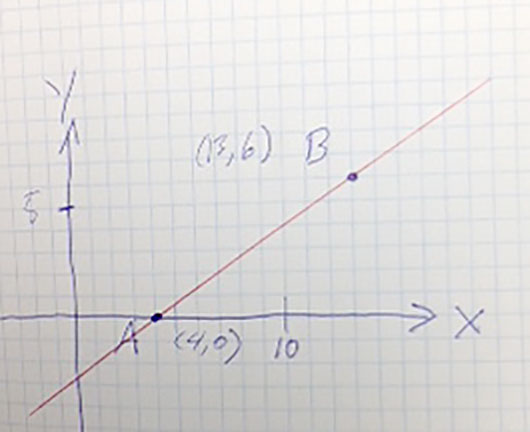
Well... It ought to be possible to find *some* of the points $P$. Consider these (leading) questions:
- How would you find the coordinates of a point which is halfway between $A$ and $B$?
- One of the points in the set $\{P\}$ should be on the line segment between $A$ and $B$. What fraction of the distance from $A$ to $B$ is that point?
- What are the coordinates of that point?
- There is one other point in $\{P\}$ along the red line, but not between $A$ and $B$. What fractional distance would it be? That is... if the distance from $A$ to $B$ were 1, what would the distance from $A$ to this second point be?
- Now we have a segment of the red line that connects two points on a circle. Either the line segment is a diameter line, or it is not. Can you make an argument for why the center of the circle could, or could not be away from the line segment?
- So, where is the center of the circle? And what is its radius?
Schlicker, 9.1 exercises
5, 8, 9