Vectors [9.2]

Sure, many physical quantities--such as the
velocity of the kayak above--have both a magnitude and a
direction.
But mathematically, vectors are key in 3+ dimensions to
generalizing ideas about lines and parallelism and
generating new concepts such as gradient and swirliness.
Vectors and scalars
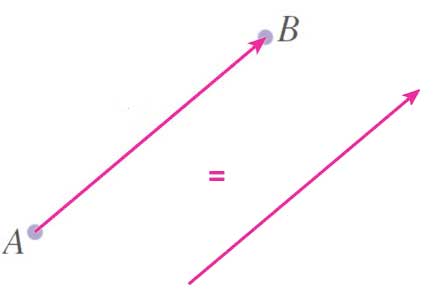
Two vectors are equal if they have the same direction
and the same magnitude. (Their positions don't matter.)
A scalar number is, for our purposes, usually the same as a real number.
A scalar number can be used to represent a quantity that does *not*
have a direction.
For example: time $t$, temperature $T$, the probability that a fish in
the ocean is a shark, $p_\text{shark}$.
Notation
Scalar quantities are typically typeset in italics: $$\nonumber t, T, p_{\text shark}$$
Vector quantities are typeset either in bold: $$ \nonumber \bf u, \bf v, \bf F $$ and/or with an arrow on the top: $$ \nonumber \myv u, \myv v, \myv F $$
I recommend that you always write an arrow over a letter to distinguish a vector from a scalar, when you're writing mathematics out by hand.
In physics
- "Speed", $v$, is a scalar. It can have a value like 30 mph or 6 ft / sec and is always a positive number.
- "Velocity", $\myv v$, is a vector quantity. The magnitude of velocity, $|\myv v|=v$, is speed. The velocity might have a magnitude like 4 meters / sec and a direction, such as north-east.
Components
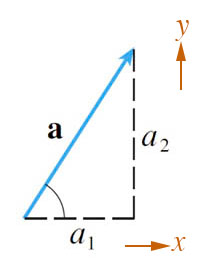 The
vector, $\myv a$, is drawn in a 2-d Cartesian coordinate system. The
difference between the $x$-coordinate of its tip and of its base is
$\Delta x = a_1$. The difference between the $y$-coordinate of its
tip and of its base is $\Delta y = a_2$. We write:
$$\myv a=\langle a_1,a_2\rangle$$
where
The
vector, $\myv a$, is drawn in a 2-d Cartesian coordinate system. The
difference between the $x$-coordinate of its tip and of its base is
$\Delta x = a_1$. The difference between the $y$-coordinate of its
tip and of its base is $\Delta y = a_2$. We write:
$$\myv a=\langle a_1,a_2\rangle$$
where
- $a_1$ (also written $a_x$) is the "$x$-component" of the vector $\myv a$,
- $a_2$ (also written as $a_y$) is the "$y$-component" of $\myv a$.
All of these vectors have the same components: $\langle 3,2\rangle$.
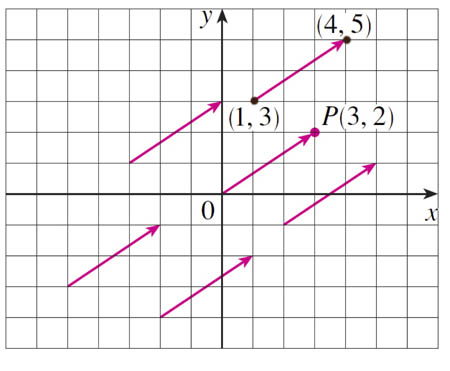
And they all have the same magnitude and direction.
A vector in standard position has its tail at the origin
What do you notice about the one vector in standard position in relation to the point at the tip of the vector?
Classroom
positions / vectors (Tanner study).
Just do $\myvv{OB}$ and
$\myvv{AB}$.
Two vectors $\myv u=\langle u_1,u_2 \rangle$ and $\myv v=\langle v_1,v_2\rangle$, are equal, if and only if their corresponding components are equal: $u_1=v_1$ and $u_2=v_2$.
Scalar multiplication
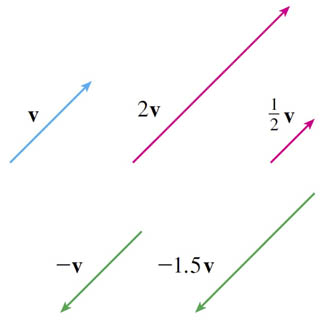
If $c$ is a scalar, and $\myv v$ is a vector, then the scalar multiple $c\myv v$ is the vector with:
- a length of $|c|$ times the length of $\myv v$, and
- a direction which is:
- the same as $\myv v$ if $c \gt 0$, or
- opposite $\myv v$ if $c \lt 0$, or
Scalar multiplication (components)
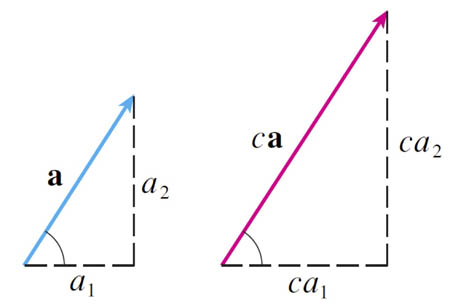
$$\myv a = \myc{a_1,a_2};\ \ \ \ c\myv a = \myc{ ca_1,ca_2 }.$$

- For each vector...Which other vectors is it parallel to?
- What relationship (involving scalar multiplication) must exist between two vectors $\myv a$ and $\myv b$ iff [if and only if] they are parallel?
Adding vectors
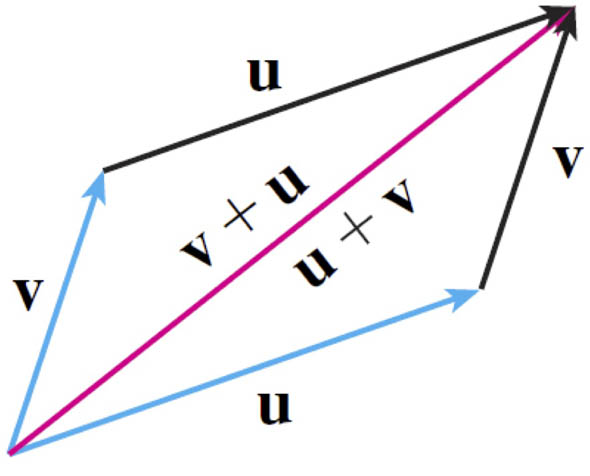
- If $\myv u$ and $\myv v$ are vectors,
- positioned such that the tale of $\myv v$ is at the tip of $\myv u$,
- then the sum $\myv u + \myv v$ is the vector from the tail of $\myv u$ to the tip of $\myv v$.
Vector subtraction
The idea is... $$\nonumber \myv u - \myv v \equiv \myv u + (-1)\myv v $$
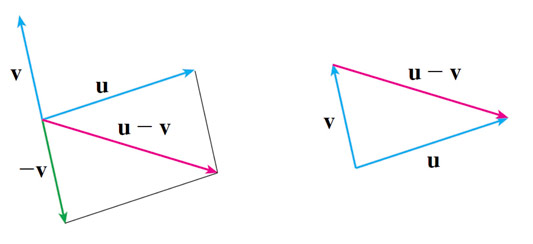
Vector addition and subtraction (components)
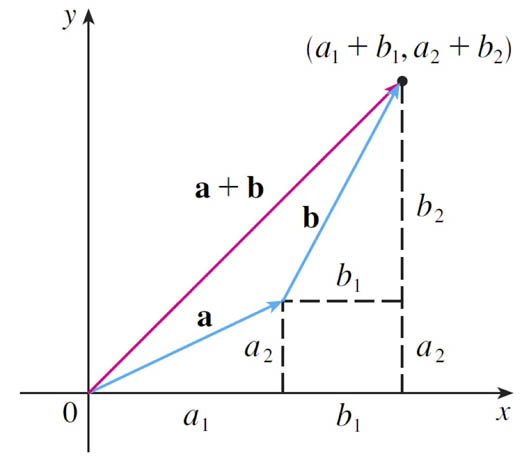
$$ \myv a + \myv b = \langle a_1+b_1, a_2+b_2 \rangle $$
Subtraction: $$ \myv a - \myv b = \langle a_1-b_1, a_2-b_2 \rangle $$
All these results generalize to 3-d.
Vector and scalar multiple addition
Length
...of a vector in terms of its components.
Length $|\myv a|$ (a scalar number) of the 2-d vector $\myv a=\langle a_1,a_2 \rangle$: $$|\myv a|=\sqrt{a_1^2+a_2^2}.$$
Length of the 3-d vector $\myv a=\langle a_1,a_2,a_3 \rangle$: $$|\myv a|=\sqrt{a_1^2+a_2^2+a_3^2}.$$
Standard basis vectors
The 3 standard "basis vectors" in a Cartesian coordinate system are: $$\myv i \equiv \langle 1,0,0 \rangle; \ \ \myv j \equiv \langle 0,1,0 \rangle; \ \ \myv k \equiv \langle 0,0,1 \rangle$$
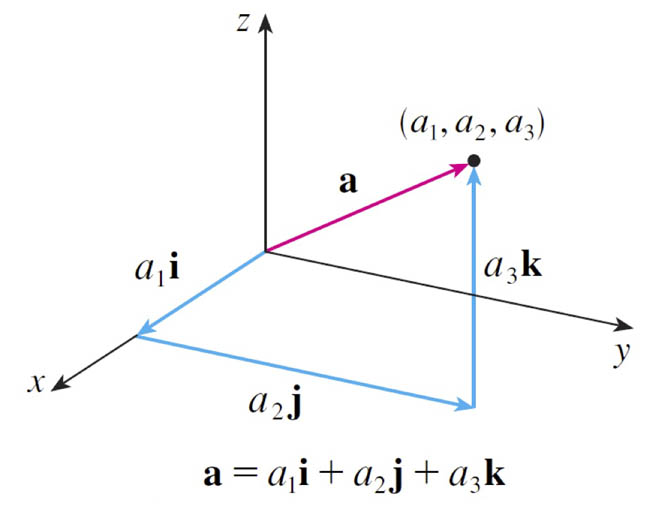
Notice that each of these vectors has a length of 1. That is, they are unit vectors.
I like to indicate unit vectors with the caret ('^') symbol up top (replacing the arrow): $$\uv i \equiv \langle 1,0,0 \rangle \equiv \uv x; \ \ \uv j \equiv \langle 0,1,0 \rangle \equiv \uv y; \ \ \uv k \equiv \langle 0,0,1 \rangle\equiv \uv z$$
Another way of writing a vector: As a sum of scalars times basis vectors: $$\langle 0.4, 0, -2 \rangle \equiv 0.4\uv i -2\uv k$$
Find the unit vectors
Find the unit vector...
- that points in the direction $\langle 8, 0, 0 \rangle$.
- that points in the direction $\langle 5,5,0 \rangle$.
- that is opposite to the direction $\langle 1,-1,3 \rangle$.
Time permitting: Unit vectors
Parallel
Two vectors, $\myv a$ and $\myv b$, are parallel if $\myv b$ is a scalar multiple of $\myv a$. That is: $$\myv b = c\myv a,$$ where $c$ is any non-zero real number.
If $\myv a$ is a vector, then a unit vector, pointing in the same direction as $\myv a$, but with a length of 1 unit is: $$\uv a = \frac {\myv a}{|\myv a|}\equiv\frac{1}{a}\myv a.$$
For example, if $\myv a=\langle 5,5,0\rangle$, then $a=\sqrt{5^2+5^2+0^2}=\sqrt{50}$, so $$\uv a= \frac {\myv a}{a}= \frac {\myc{5,5,0}}{\sqrt{50}}= \myc{ \frac{5}{\sqrt{50}},\frac{5}{\sqrt{50}},0}.$$ Checking the length of $\uv a$: $$\begineq |\uv a| &=\sqrt{\frac{5^2}{(\sqrt{50})^2} +\frac{5^2}{(\sqrt{50})^2} + 0^2}\\ &=\sqrt{\frac{25}{50} +\frac{25}{50}}=\sqrt{\frac{50}{50}}=1 \endeq$$
Using the vectors (not necessarily unit vectors) $\myv b = \langle 1,0\rangle$ and $\myv c = \langle 1,2\rangle$, try to express and $\myv a$ as $r\myv b + s\myv c$.