Dot product [9.3]

No, no, not those kind of dots...
How effective is a force at moving a cart along a road?
Consider pushing a cart, with the same force, $F=100N$, (the same force as the weight of a 10 kg bowling ball)
but in different directions: (The blue vector is the direction we'd like the cart to move: along (parallel to) the road.)

Brian Evans
- parallel to the road;
- at right angles to the road;
- at some intermediate angle $\theta$ (say $45^{o}$) to the road.
Which direction is most effective at moving the cart? 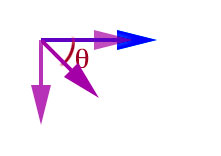
We'd like to multiply the force by some function of the angle that is greatest when $\theta=0$ and least (actually zero) when $\theta=\pi/2$
and "somewhat" effective when $\theta=\pi/4$.
How about: $$F\cos\theta??$$
$\cos \theta$ is a measure of how closely aligned two directions are (given by the directions of two vectors).
I'm trying hard not to say parallel...
How much energy?

"Work" in physics is the energy expended when a constant force $\myv F$ acts to displace an object by a vector displacement $\myv d$. It seems like this "Work" should depend on
- The force, $F$,
- how far we move it: the displacement, $d$,
- and how parallel $\myv F$ and $\myv d$ are to each other, $\cos\theta$.

Work is the product of the displacement and the component of the force along the direction of the displacement. $$\nonumber \text{Work}=F_d d = (F \cos \theta) d=Fd\cos\theta.$$We shall see shortly that this can be written as $$\text{Work}=\myv F \cdot \myv d.$$ [Units: Newton-meter = Joule]
So... If the force is at right angles to the displacement no work is done? Can you think of an example?
Component
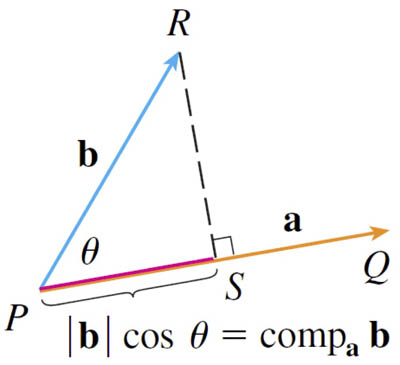
The component of $\myv b$ along $\myv a$ is a scalar: $$\text{comp}_{\myv a}\myv b = b \cos \theta.$$ ...also called the scalar projection.
Projection
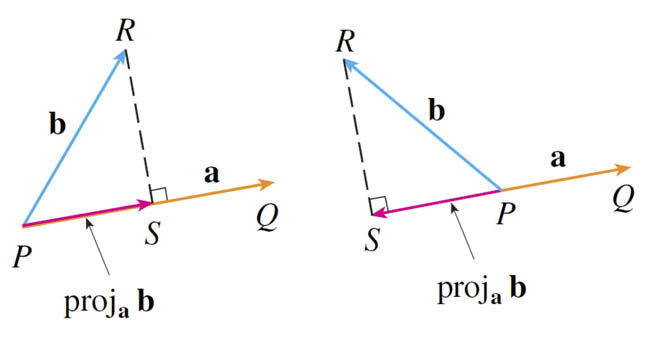
The vector projection of $\myv b$ along $\myv a$ is a vector which points along $\myv a$ and has a length of $b\cos\theta=\text{comp}_{\myv a}\myv b$.
Get the 09.3.Projections activity from the handouts folder. Work on the first two parts.
The dot product
...of two non-zero vectors $\myv a$ and $\myv b$ is defined as $$\myv a \cdot \myv b \equiv |\myv a| |\myv b| \cos \theta$$ where $\theta$ is the smallest possible angle between the vectors when they're drawn with the same initial point. That is, $0 \leq \theta \leq \pi$.
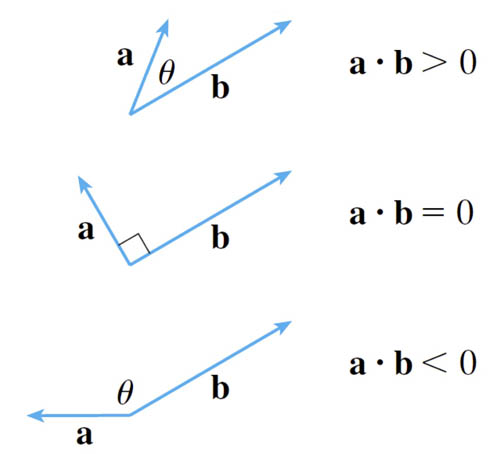
Two vectors are orthogonal (which is a general way of saying "perpendicular") if and only if their dot product is zero. $$\myv a \cdot \myv b=0 \ \ \Leftrightarrow \ \ \myv a \perp \myv b.$$
Component form
The dot product of $\myv a=\langle a_1,a_2,a_3\rangle$ and $\myv b=\langle b_1,b_2,b_3\rangle$ can be written in terms of their components: $$\myv a \cdot \myv b = a_1b_1+a_2b_2+a_3b_3.$$ Examples:
$$\nonumber \langle 2,4 \rangle \cdot \langle 3,-1\rangle = 2(3)+4(-1)=2$$
$$\nonumber \langle -1, 7, 4\rangle \cdot \langle 6,2,\frac 12\rangle = -1(6)+7(2)+4(\frac 12)=10$$
$$\nonumber (\myv i + 2\myv j -3\myv k)\cdot(2\myv j -\myv k)=1(0)+2(2)-3(-1)=7$$
Could also multiply out the product in that last one, and show how orthogonality is used.
Properties of the dot product

Components and Projections re-visited
Component

The component of $\myv b$ along $\myv a$ is a scalar: $$\text{comp}_{\myv a}\myv b = b \cos \theta = \frac{|\myv a|}{|\myv a|} |\myv b| \cos \theta = \frac{\myv a \cdot \myv b}{|\myv a|}.$$

The vector projection of $\myv b$ along $\myv a$ is a vector which points along $\myv a$ and has a length of $b\cos\theta=\text{comp}_{\myv a}\myv b$.
We can construct a vector, $\uv{a}$ of unit length pointing in the $\myv a$ direction like this: $$\uv{a}=\frac{\myv a}{|\myv a|}$$
The vector projection is: $$\text{proj}_{\myv a}\myv b = b\cos\theta \uv a = \frac{\myv a \cdot \myv b}{|\myv a|^2}\myv a.$$
To do
- The Regular Hexagon (see the handouts folder)
Image credits