Lines and planes [9.5]

Casa Batlló by Antoni, "enemy of the straight line" Gaudí and Josep Maria Jujol.

Vector form of a line

It seems like "two points determine a line" should work in three dimensions as well as in 2-d. But we may have hit a dead end with $y=mx+b$: It's not obvious what the "slope" is in 3-d. It's certainly not a scalar number.

In the preview activity, you became acquainted with a new way of describing a line, that still works in 2-d but generalizes to 3-d more easily. The line that passes through 2 points $P$ and $Q$...

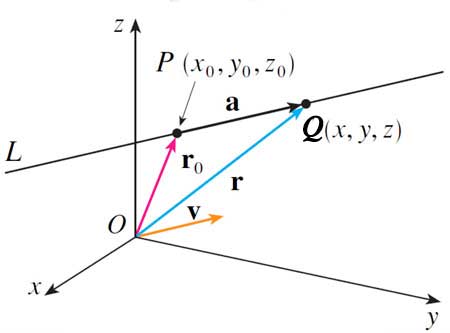
• $\myvv{OP}=\myv r_0$ is the position vector of a point on the line with tail at the origin, and head at point $P=(x_0,y_0,z_0)$.
• $\myvv{PQ}\equiv \myv a$ is the difference vector, which runs from $P$ to some other point $Q$, both on the desired line.
• $\myv v=\langle a,b,c\rangle$ is the direction vector, and it is parallel to $\myv a$.
• Any vector parallel to $\myv v$ can be expressed as some scalar multiple $t\myv v$ of $v$.

So, using vector addition, we can express the set of points on the line in parametric form (as a function of the parameter $t$) as:

Vector form of a line $$\myv r(t)=\myv r_0 + t\myv v$$

• If you know any two points on a line, say $P$ and $Q$, you can use the difference vector $\myvv{PQ}$ as your direction vector.
• Even in 2-d, we could use this form to describe vertical lines, e.g. using $\myv v=\langle 0,1\rangle$, something we can't do with $y=mx+b$.

Do Activity 9.5.2. Parallel lines?

The parametric equations of a line

$$\begineq \myv r(t) &= \myv r_0 + t\myv v \\ &= \langle x_0,y_0,z_0\rangle+t\langle a,b,c\rangle \\ \langle x(t), y(t), z(t)\rangle&= \langle x_0+ta, y_0+tb, z_0+tc \rangle .\endeq $$

We know that a 3-d vector equation is really *3* equations. In order for two vectors to be equal, their $x$-, $y$-, and $z$-components must each be equal. The three equations here are:

Parametric equations for a line $$x(t)=x_0 +at;\ \ y(t)=y_0 +bt;\ \ z(t)=z_0 +ct$$

Each of these 3 can be solved for $t$, e.g. $\frac{x(t)-x_0}{a}=t$. We'll have three expressions each equal to $t$, so we can set them mutually equal:

Symmetric equations of a line $$\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}.$$

• Notice that $a$, $b$, $c$ are the components of $\myv v$, the direction vector parallel to the line $L$.
• These are something like the point-slope form of the equation of a line in 2-d. Indeed, the first two equations for a 2-d line can be arranged like this: $$\frac{y-y_0}{x-x_0}=\frac ba \equiv m.$$

  A 9.5.3 Is a point on the line?

  Example

  Consider two lines: $$\nonumber x=1+t;\ \ y=-2+3t;\ \ z=4-t$$ and $$\nonumber x=2s;\ \ y=3+s;\ \ z=-3+4s$$

  Do they intersect?

  Solution: If they intersect at some common point (x,y,z), then that point should be a simultaneous solution in $s$ and $t$ to these three equations: $$1+t=2s;\ \ -2+3t=3+s;\ \ 4-t=-3+4s$$

  Those same two lines: $$\nonumber x=1+t;\ \ y=-2+3t;\ \ z=4-t$$ and $$\nonumber x=2s;\ \ y=3+s;\ \ z=-3+4s$$

  Are the lines parallel?

  Solution: Re-arrange the equations into the form of the symmetric equations (solve each equation for $t$...or for $s$...) to find the components (denominators) of a vector parallel to each line.

  Lines which are not parallel to each other, and do not intersect are called skew lines.

  To do

  • Lines in the plane

  Planes

  A plane can be determined by

  • a point $P_0$ in the plane and
  • a normal vector, $\myv n$, which is orthogonal (normal) to the plane.

  In pictures...
  

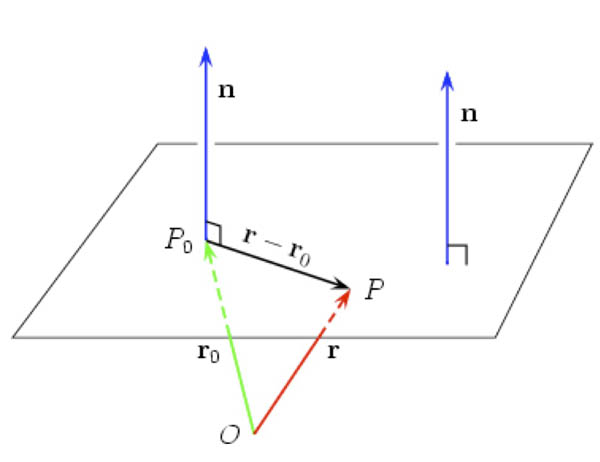
  • $\myv r_0=\langle x_0, y_0, z_0 \rangle$ is a vector pointing at $P_0$.
  • $\myv n = \langle\color{blue}a, b, c\color{black} \rangle$ is the normal vector.
  • $\myv r=\langle x,y,z\rangle$: Some point in the plane, which must satisfy the condition that $\myv r -\myv r_0$ is perpendicular to $\myv n$:

  With these definitions:

  Equations of a plane: $$\begineq \text{"vector" eq:}\ \ \ \ 0&=\myv n \cdot (\myv r-\myv r_0)\\ &=\langle \color{blue}a,b,c\color{black} \rangle \cdot \langle x-x_0,y-y_0,z-z_0\rangle\\ \text{"scalar" eq:}\ \ \ \ 0&=\color{blue}a\color{black} (x-x_0)+\color{blue}b\color{black}(y-y_0)+\color{blue}c\color{black}(z-z_0)\rangle\\ \endeq $$

Pushing the equation above one step further, let's expand the products and add up all the constant terms calling their sum $k=\myv n\cdot\myv r_0$: $$\begineq ax_0+by_0+cz_0&=ax+by+cz\\ k&=ax+by+cz \endeq $$

So that if you see an equation for a plane such as: $$56=7x-3y+2z,$$ You can just read off the components of a normal vector to the plane as: $$\myv n=\langle 7,-3,2 \rangle.$$

Do Problem 7 - Angle between planes.

Example

A plane intersects the $x$-, $y$-, and $z$-axes at the points shown. Find the equation of the plane.

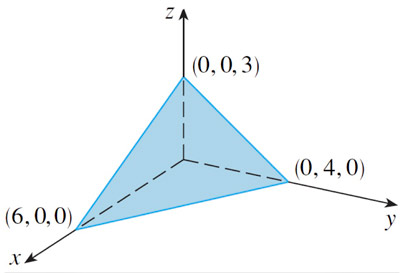
First find the normal to the plane.
[Find two vectors that are in the plane, and then take their cross product.]

Then find the equation for the plane. [Take as $\myv r_0$ any of the three points shown.]

Find the surface normal:
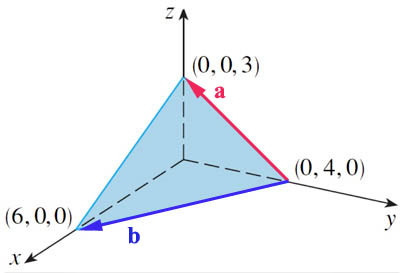$\myv a=\langle 0,-4,3 \rangle$
$\myv b=\langle 6,-4,0 \rangle$
$\myv a \times \myv b=12\uv i+18\uv j+24\uv k$

Let's take for the normal vector $\frac16$ of the the vector above (just because we'll have smaller numbers to keep track of...): $$\myv n=2\uv i+3\uv j+4\uv k =a \uv i + b \uv j +c \uv k$$

Picking $(0,4,0)$ as the point in the plane, then the prescription above is... $$\begineq 0 &=a(x-x_0)+b(y-y_0)+c(z-z_0)\\ &=2(x)+3(y-4)+4(z) = 2x+3y-12+4z\\ \endeq$$ So, the equation for the plane can be written as: $$2x+3y+4z = 12.$$ where a normal vector to the plane was $\myv n=\myc{2,3,4}$.

Notice that when the equation for a plane is written in this form that you can read off the components of the normal vector from the coefficients of $x$, $y$, and $z$!

Image credits

vgm8383