Vector functions [9.6]
Curves in space.

Blessing of the media, Soyuz launch 2013 [NASA]
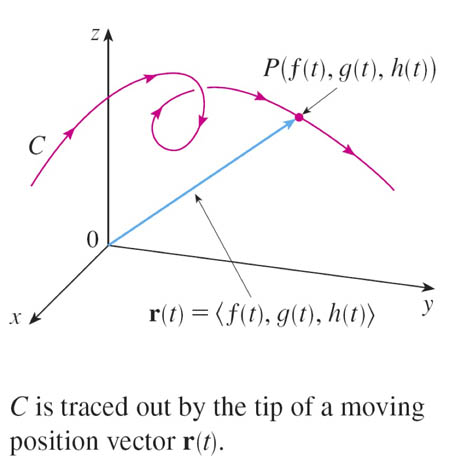
A curve in space can be described as the path of the tip of a position vector $\myv r(t)$: $$\myv r(t)=\langle x(t), y(t), z(t)\rangle,$$ which is a function of a single parameter.
For example: A line
Animation of the parametric equation, $$\begineq\myv r(t)&=(-1.34,1.32, 0)+t \langle 2/3,-1/3,2/3 \rangle\\ &=(-1.34,1.32, 0)+t \myv v \endeq$$ of a line. We'll often use a parameter named $t$ or $k$.
Parametric vector functions
But we're not limited to lines. Consider the animation of the equation for the position vector $\myv r(t)$: $$\myv r(t)= \langle \cos t, \sin 2t, 0.3+\sin(t)\cos(t) \rangle$$
The position of an object in
3-d, as a function of time,
$\myv r(t)$ is an example of a vector function.
In GeoGebra type (or copy and paste): (sin(t),cos(t),sin(t) cos(t)) and notice the curve that appears, and the way GeoGebra changes what you've typed in, and adds some default values...
Vector functions and parametric equations
Consider the 2-d vector function: $$\myv r(t)=\langle t,t^2\rangle$$
- $\myv r(t)=\langle t,t^2 \rangle$
- $x(t)=t;\ \ \ y(t)=t^2$
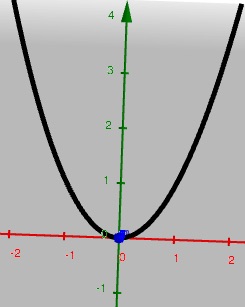 In this case we can write $y$ as a function of $x=t$:
$$\nonumber y=x^2$$
and we know what that looks like...
In this case we can write $y$ as a function of $x=t$:
$$\nonumber y=x^2$$
and we know what that looks like...
In GeoGebra: we can make parametric plots, by specifying functions for the $x,\ y$ and $z$ coordinates of a position vector in terms of a common parameter, for example, the parameter $t$, like this
( [x(t)], [y(t)], [z(t)] )
For example
(t,t^2,0)is a parametric plot, where $x(t)=t;\ y(t)=t^2;\ z(t)=0$, where $t$ runs over all possible values.Curve(t,t^2,0, t,0,10)is a portion of the parametric plot above, limited to a restricted domain of parameter values: $0 \lt t \lt 10$. >
Try it out!
Parametric plotting of expressions in polar coordinates
Remember polar coordinates?
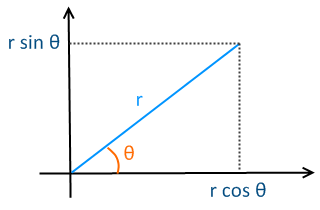
Going from Cartesian coordinates, $(x,y)$ to polar coordinates:
$$r=x^2+y^2;\ \ \ \ \theta=\arctan\left(\frac yx\right),$$
and the other way...
$$x=r\cos\theta;\ \ \ \ y=r\sin\theta$$
It is frequently useful to remember that
$$\sin^2\theta+\cos^2\theta=1.$$
Finding a "parameterization" of a curve
A common problem is:
Given an equation for a curve, say $x=y^2$ or $x^2+y^2=4$... Can you find a way to parameterize the equation? That is, express it in terms of parametric expressions for each of the coordinates, $\langle x(t),y(t)\rangle$?
For examples above....
- E.g. $x=y^2$: If one coordinate is given in terms of the other...Let one of the coordinates be the parameter: $$ y(t)=y; \ \ \ x(t)=t^2 .$$
- E.g. $x^2+y^2=4$. Use some geometrical relationship: We know that this is the equation for a circle of radius 2. We can use polar coordinates to describe the the coordinates of the points on the circle in terms of the angle $\theta\to t$:
$$ x(t)=2\cos t; \ \ y(t)=2\sin t;\ \ 0\lt t \lt 2\pi $$
GeoGebra expects you to specify functions in terms of Cartesian coordinates anyway, and implicitly assumes that the name of your parameter will be '$t$'. So,
( 2*cos(t), 2*sin(t), 0 )Will plot a circle in the $xy$ plane of radius 2.
Can you imagine what these functions look like?
Guess first, and then plot in Geogebra to confirm: $$\myv r(t)=\langle t\cos t, t\sin t, 0\rangle?$$ $$\myv r(t)=\langle \cos t, \sin t, t\rangle?$$Do the 'paraboloid' activity (9.6.4).
c.) Use polar coordinates to parameterize this curve in terms of $\theta=t$.
d.) To find the level curve for $z=25$, use polar coordinates to parameterize in terms of $t=\theta$. But what to make of their hint??? Instead: Convert $x$ and $y$ to polar coordinates; and then substitute $\cos^2 \theta\to 1-\sin^2\theta$. Now solve for $r(\theta)$. There's a square root. What angles is $r(\theta)$ defined for? For what 4 angles does $r(\theta)\to \infty?$ Now evaluate $r(0)$ and $r(\pi)$ and sketch $r(\theta)$.Plotting and visualizing curves in 3 dimensions
Consider this curve: $$\myv r(t)=\langle \cos t, \sin t, t\rangle\nonumber$$ If we *ignore* the $z$ coordinate (or, think of just setting it to 0), we'll have this simpler parametric equation: $\myv r(t)=\langle x(t),y(t)\rangle = \langle \cos t, \sin t \rangle$. You might recognize this as the equation for the unit circle. The tip of the vector will trace out all the points on a circle of radius 1 as $0 \lt t \lt 2\pi$.
- So in 3-d, the path traced out by $\myv r(t)$ must lie on the surface of the cylinder $x^2+y^2=1$
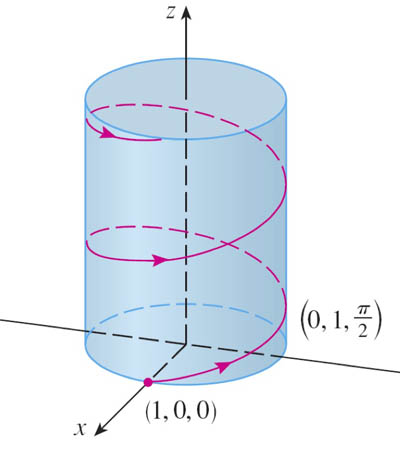
This process of ignoring one coordinate, and seeing how 2 of the coordinates relate to each other without regard to the other one is "projection". Doing this with the other coordinate pairs, we see the familiar-looking relations: $$\nonumber x=\cos z;\ \ \ y=\sin z$$
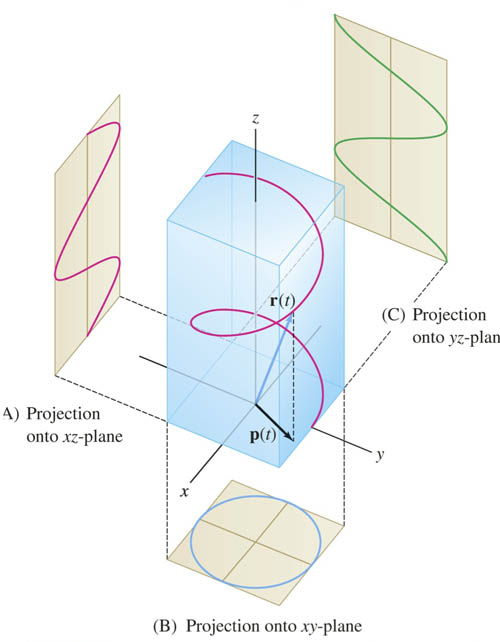
To Do
- Handout: 09.6.ProjectionsOfCurves
Intersections and projections
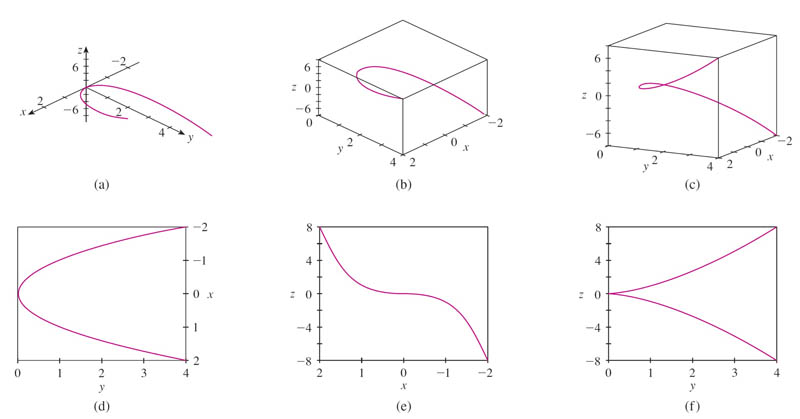
Consider $$\myv r(t)=\langle t,t^2,t^3 \rangle \nonumber$$
Since $y(t)=t^2$ and $x(t)=t$ we can combine these equations to get $$\nonumber y=x^2.$$
And similarly $$\nonumber z=x^3,$$ so we could plot the 3-d surfaces
- $y=x^2$ (for any $z$), and
- $z=x^3$ (for any $y$)
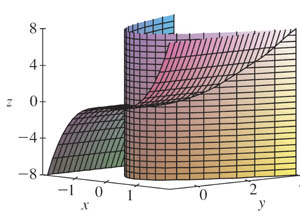 The points in $\myv r$ need to be on *both* of those surfaces, so we could look for $\myv r$ as the intersection of the surfaces.
The points in $\myv r$ need to be on *both* of those surfaces, so we could look for $\myv r$ as the intersection of the surfaces.
Projections of $\langle t,t^2,t^3 \rangle$