Derivatives and integrals of vector functions [9.7]

Derivatives
In Calc I, we defined the derivative as the limit of a "Difference Quotient": $$f'(x)=\lim_{h\to 0} \frac{f(x+h)-f(x)}{h}.$$
For a vector function, $\myv r(t)$, there's a similar difference quotient: $$\frac{d\myv r}{dt} \equiv \myv r'(t) = \lim_{h\to 0} \frac{\myv r(t+h)-\myv r(t)}{h}.$$
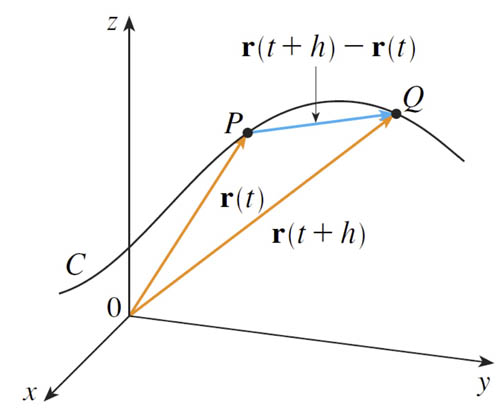
In the limit $h \to 0$, $\myv r'(t)$ is a vector which is tangent to the curve at $\myv r(t)$.
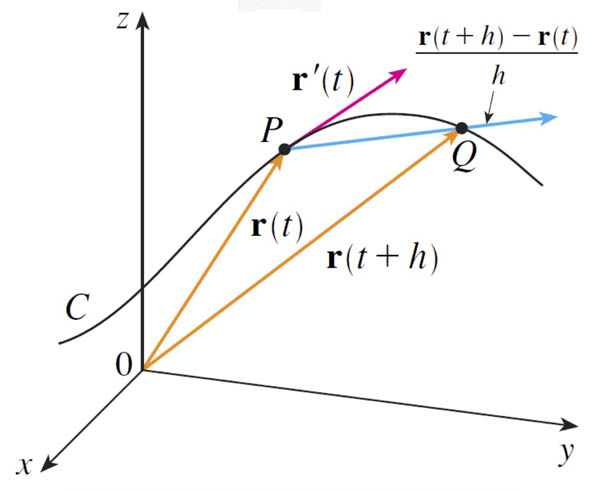

Try out this Difference Quotient (DQ) visualization (GeoGebra).
When $t=2.5$,
points $P$ and $Q$ are points at the tip of position vectors:
$$P=\myv r(2.5); \ \ \ Q=\myv r(2.5+h)\nonumber.$$
The difference vector is:
$$\color{blue}\mathsf{diff}=\myvv{PQ}=\myv r(2.5+h)-\myv r(2.5)$$
and the difference quotient is:
$$\color{red}\mathsf{DQ}=\frac{\mathsf{diff}}{h}=\frac{\myv r(2.5+h)-\myv r(2.5)}{h}$$
and the derivative is
$$\left.\myv r'(t)\right|^{t=2.5} = \lim_{h\to 0}\frac{\myv r(2.5+h)-\myv r(2.5)}{h}.$$
Differentiation - components
A theorem: if $\myv r(t)=\langle f(t),g(t),h(t)\rangle = f(t)\uv i+g(t)\uv j+h(t) \uv k$, where $f$, $g$, and $h$ are differentiable functions, then $$\myv r'(t)=\langle f'(t),g'(t),h'(t)\rangle = f'(t)\uv i+g'(t)\uv j+ h'(t)\uv k.$$
Do 9.7.3, Calculating derivatives, a. and d.
Differentiation rules

- $\myv r'(t)\equiv \myv v(t)$
The first derivative of position with respect to time, $t$,
is the object's velocity, $\myv v(t)$. - $\myv r''(t)=\myv v'(t)\equiv \myv a(t)$
The second derivative of position wrt $t$,
is the first derivative of velocity wrt $t$,
is the object's acceleration, $\myv a(t)$.
Do A 9.7.4, velocity and acceleration
Cusp?
A vector function $\myv r(t)=\myc{f(t),g(t),h(t)}$ might have a cusp if, at some time $t$ exists such that $\myv r'(t)$ is a zero vector.
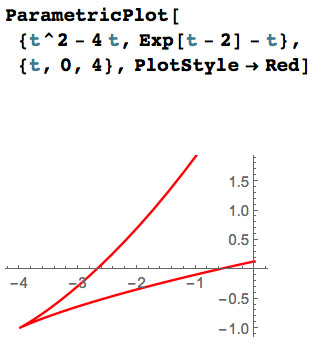 At right: $\myv r(t)=\myc{t^2-4t,e^{t-2}-t}$, so
$\myv r'(t)=\myc{2t-4,e^{t-2}-1}$.
At right: $\myv r(t)=\myc{t^2-4t,e^{t-2}-t}$, so
$\myv r'(t)=\myc{2t-4,e^{t-2}-1}$.
And... $\myv r'(2)=\myc{0,0}$.
Tangent lines

The line, $L$, tangent to the curve at $\myv r(t_0)$ is: $$\myv L(t) = \myv r(t_0) + t \myv r'(t_0).$$
Do A 9.7.5, Tangent line. Use Geogebra to graph $\myv r(t)$. Put a point at $\left.\myv r(t)\right|^{t=\pi}$. Calculate $\myv r'(t)$ by hand. Then plot the vector $\left.\myv r'(t)\right|^{t=\pi}$, with its tail at $\left.\myv r(t)\right|^{t=\pi}$.
The unit tangent vector is given by: $$\uv T(t) = \frac{\myv r'(t)}{|\myv r'(t)|}.$$
Theorem: If a vector function, $\myv r(t)$, has constant length, then its derivative, $\myv r'(t)$, is perpendicular to $\myv r(t)$.
Proof:
- We're assuming that the length of $|\myv r(t)|$ is not changing. That is, $$\frac{d}{dt}|\myv r(t)|=0.$$
- Then, (length)${}^2$ is also unchanging: $$\begineq 0&=\frac{d}{dt}|\myv r(t)|^2\\ &=\frac{d}{dt}(\myv r\cdot\myv r)=\myv r'\cdot \myv r+\myv r\cdot\myv r'\\ 0 &=2\myv r'\cdot \myv r\\ \endeq $$
- Since the dot product of $\myv r'$ and $\myv r$ is zero, $\myv r' \perp \myv r$.
Example: $\myv r(t)=\langle cos(t),sin(t)\rangle$. Taking the derivative of its component functions... $$\nonumber \myv r'(t)=\langle -\sin(t),\cos(t)\rangle.$$ The magnitude of this derivative vector is $$|\myv r'(t)|=\sqrt{(-\sin t)^2+\cos t)^2}=\sqrt{\sin^2 t+\cos^2 t} = 1.$$ We see that the magnitude of the derivative is a constant (not changing with $t$).
See Circular motion (GeoGebra)
The unit tangent
- The Unit Tangent $\uv T(t)=\frac{\myv r'(t)}{|\myv r'(t)|}$ has constant length 1.
- The only characteristic of $\uv T(t)$ that changes as $t$ changes is its direction.
- $|d\uv T/dt|$ measures the rate of change of the direction of the unit tangent vector. ["units" are radians per $t$-unit].
Example: $\myv r(t)=\langle t^3,t^6\rangle$
Integrals
$$\begineq \int_a^b \myv r(t)\,dt &= \int_a^b \langle f(t),g(t),h(t)\rangle\,dt\\ &= \left(\int_a^b f(t)\,dt\right)\uv i + \left(\int_a^b g(t)\,dt\right)\uv j + \left(\int_a^b h(t)\,dt\right)\uv k\\ \equiv& \myv R(t). \endeq $$
These are the components of $\myv R(t)$, the anti-derivative of $\myv r(t)$: $$\int_a^b \myv r(t)\,dt = \left. \myv R(t)\right|_a^b = \myv R(b)-\myv R(a). $$ And $\myv R'(t)=\myv r(t)$.
To do
Do (in the mvhandouts folder) 09.7.GrimReaper - the grim reaper.
Projectile motion
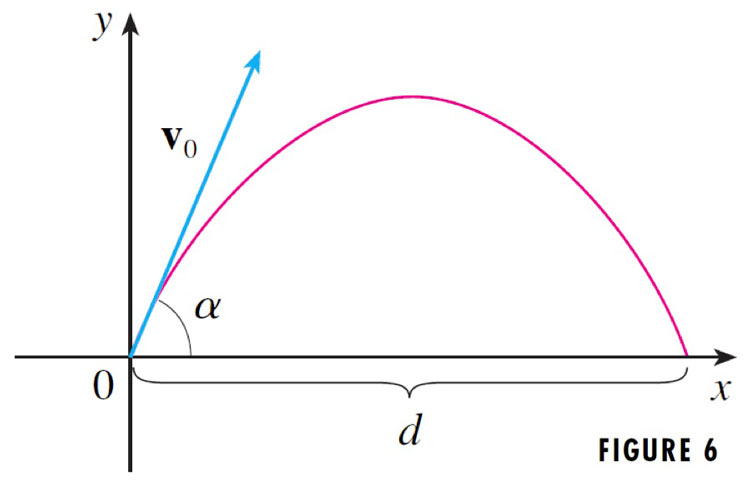
Acceleration due to gravity is constant, and always *down*.
Newton's law, $\myv F=m\myv a$: The only force acting on the projectile is gravity. The gravitational force is the object's weight, $mg$ (where $g=9.8$ m/s${}^2$). $$\myv F= m(a_x(t) \uv i+a_y(t) \uv j=-mg \uv j =\myc{ 0, -mg}.$$
Assuming that a projectile is launched at $t$ from the origin in the diagram above, we have: $$\myv r(0)=\myc{0,0}$$ $$\myv v(0)=\myc{v_0\cos\alpha,v_0\sin\alpha}.$$
In the vertical direction ($\uv j$ component) this becomes: $$-g=a_y(t)=v_y'(t)$$ Integrating as above and saying that $t=0$ is the time of launch (so that $v_y(0)=v_0\sin\alpha$ and $v_x(0)=v_0\cos\alpha$) we get: $$v_y(t)=v_0\sin\alpha-gt.$$ Integrating once more, as above, gives: $$y(t)=(v_0\sin\alpha) t-\frac12gt^2.$$
Going through a similar process, the horizontal position is found to be: $$x(t)=(v_0\cos\alpha) t.$$