Arc length (and curvature) [9.8]

The Nowitna river (Alaska) - How long is it?
a
- Calculating arclength and curvature
- Arclength is independent of the choice of parameter used to describe a curve.
- Re-parameterizing a curve - using the arclength as the parameter.
- Geometric definition of curvature.
- The TNB frame (Tangent - Normal - Binormal unit vectors).
- Tangent and Normal components of acceleration
Arclength
You know some special-case formulas for calculating the distance along a straight line between 2 points, or the perimeter of a circle.
But now that you know how to describe *any* continuous curve in space with parametric equations, we'll develop a general way to integrate to find the distance along *any* continuous curve in space.
$\myv r(t)$ is a vector function.
$$\myv r(t)=\langle f(t),g(t),h(t)\rangle\nonumber;
\ \ t_i\leq t\leq t_f.$$
where $\myv r(t_i)=\myv a$ and $\myv r(t_f)=\myv b$
The tip of the position vector $\myv r(t)$ traces a curve (trajectory) in space which
looks schematically like:
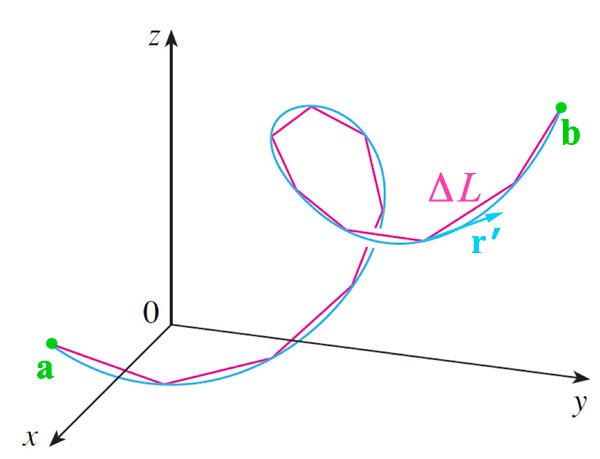
- The arclength is the distance along the curve from $\myv a$ to $\myv b$.
- Arclength is a scalar.
- It is not the distance "as the crow flows" of a vector starting at $\myv a$ and terminating at $\myv b$.
- $\myv a\equiv \myv r(t_i)$ and $\myv b\equiv \myv r(t_f)$.
The arclength from $\bf{a}$ to $\bf{b}$ is approximately equal to the sum of the The derivative $\myv r'(t)$ is a vector tangent to the curve. Its magnitude is the "speed" of a particle moving in time, $t$, according to $\myv r(t)$. So, the arclength is approximately
$$L\approx \sum |\myv r'(t)|\Delta t\nonumber.$$
In the limit of ever smaller $\Delta t\to dt$, the sum approaches the integral...
$$\begineq L&=\int_{t_i}^{t_f} |\myv r'(t)|\,dt\\
&=\int_{t_i}^{t_f} \sqrt{\left(\frac{df}{dt}\right)^2
+ \left(\frac{dg}{dt}\right)^2
+ \left(\frac{dh}{dt}\right)^2
}\,dt
\\
&=\int_{t_i}^{t_f} \sqrt{\left(f'(t)\right)^2
+ \left(g'(t)\right)^2
+ \left(h'(t)\right)^2
}\,dt
\endeq
$$
$$s(t) = \int_0^t |\myv r'(t)|\, dt
=\int_0^t\sqrt{\left(\frac{dx}{dt}\right)^2 +
\left(\frac{dy}{dt}\right)^2+
\left(\frac{dz}{dt}\right)^2
}
\,dt$$.
Taking the derivative w.r.t. $t$ of both sides, this means that
$$\frac{ds}{dt}=|\myv r'(t)|.$$
...though some
well-regarded textbooks (Stewart!) write "parametrization".]
The two parametric curves above are plotted here (GeoGebra) (one as a point, and one as the tip of a position vector). Discuss with a partner:
It may be useful (and is certainly beautiful) to re-parameterize a curve in terms of
the arclength along a curve
We could use the arclength ("distance along the curve") as the parameter to describe a curve (instead of the time, or angle, or some other parameter).
Example -- $\myv r(t)=\langle \cos t,\sin t,t\rangle$:
Reparametrize with respect to arc length, beginning at (1,0,0) in direction of increasing $t$.
This depends on being able (easily or otherwise) to take $s(t)$ and invert it to $t(s)$.
This is a technique used in General Relativity: We talk about the "proper time" measured along the the space-time trajectory of a particle as a quantity that all observers agree on.
Since distance = speed (times) time, we can approximate the distance $\Delta L$ moved in a time interval $\Delta t$ as
$$ \Delta L \approx \left| \myv r'\right| \Delta t\nonumber$$
Example
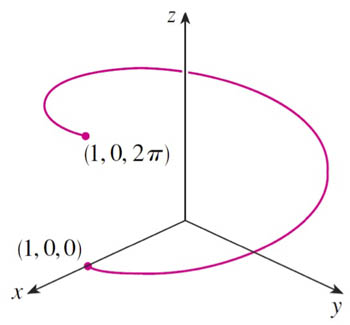 Find the length of the arc of the helix that obeys the equation
$$\nonumber \myv r(t)=\langle \cos t, \sin t, t \rangle$$
from the point $(1,0,0)$ to $(1,0,2\pi)$.
Find the length of the arc of the helix that obeys the equation
$$\nonumber \myv r(t)=\langle \cos t, \sin t, t \rangle$$
from the point $(1,0,0)$ to $(1,0,2\pi)$.
It looks like
$$ 0 \leq t \leq 2\pi.$$
Estimating first: Before you do the problem, what is the arclength around $\myc{\cos t, \sin t, 0}$ over that same interval $0\leq t\leq 2\pi$? Will the answer to your problem above be greater than or less than this answer?
Substituting into the arclength expression
$$L =\int_0^{2\pi} \sqrt 2 \,dt=\sqrt 2 2 \pi.\nonumber$$
Arclength distance function
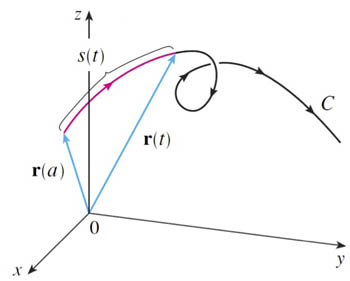 The arclength distance function $s(t)$, where $s(0)=0$,
The arclength distance function $s(t)$, where $s(0)=0$,
Parameterizations
Re-parameterization
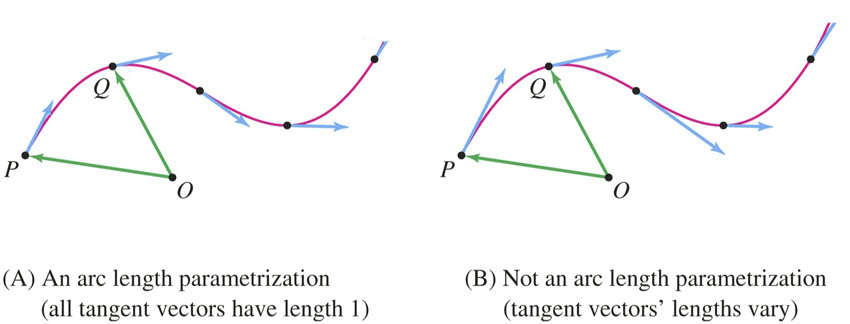
Image credits