Curvature
The question: How to describe "curvature" in a useful way?
The curvature should be...
- a scalar number which should be
- large when the path is changing direction "quickly",
- small when the path is more nearly straight.
The velocity vector $\myv r'(t)$ is tangent to the curve at each position on the curve. So, as the direction of a curve changes,the velocity vector will also change. So our first attempt to quantify the idea of "curvature" might be to look at at the change of the velocity vector, that is, the acceleration:
$$\myv a (t)= \frac{d\myv r'(t)}{dt}$$
Can you think of a situation in which the acceleration is not zero, even though the curvature of the path is zero?
Acceleration in a straight line.
The unit tangent $$\uv T(t)=\frac{\myv r'}{|\myv r'|}$$ is a vector quantity that is always the same length, no matter what the velocity $\myv r'$ is. So, what about $$\frac{d\uv T(t)}{dt}?$$ What's the problem with that?
In this picture, the unit tangent vectors are evenly spaced along the curve:
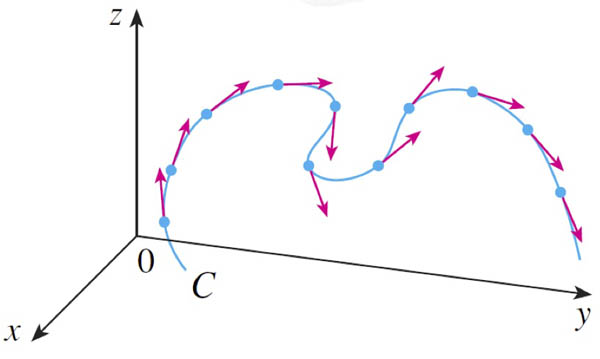
Does this suggest a useful way to think about curvature?
...We should look at how $\uv T$ changes with respect to changes in the arclength, $s$, (instead of w.r.t time $t$):
The curvature, $\kappa$, is $$\kappa = \frac{d\uv T}{ds},$$ the rate of change of unit tanget vector direction with respect to arclength.
By the chain rule, this is $$\kappa = \left|\frac{d\uv T}{dt}\right| \frac{dt}{ds} =\frac{\left|\frac{d\uv T}{dt}\right|}{ \frac{ds}{dt} }= \frac{|\uv T'(t)|}{|\myv r'(t)|} .$$
Curvature of a circle
It seems like a circle ought to have a constant curvature. Let's see...
Circle of radius $a$: $$\nonumber\myv r(t)=a \cos t\uv i + a \sin t\uv j.$$
$$\nonumber\myv r'(t)=-a\sin t \uv i + a \cos t\uv j.$$
$$\begineq\nonumber|\myv r'(t)| &= \sqrt{(-a\sin t)^2+(a\cos t)^2}\\ &=\sqrt{a^2\sin^2 t+a^2\cos^2 t}\\ &=a\sqrt{\sin^2t+\cos^2t}=a\endeq$$.$$
$$\nonumber\uv T(t) = \myv r'(t)/|\myv r'(t)|=\myv r'(t)/a=- \sin t \uv i+\cos t\uv j.$$
$$\nonumber\uv T'(t) =- \cos t \uv i - \sin t\uv j.$$
$$\nonumber|\uv T'| = \sqrt{(-\cos t)^2 +(-\sin t)^2}=\sqrt{\cos^2 t+\sin^2 t} = 1.$$
$$\kappa = \frac{|\uv T'(t)|}{|\myv r'(t)|}=\frac{1}{a}.$$
- The curvature $1/a$ is constant, independent of $t$.
- Small circles have a large curvature, and
- large circles have a small curvature.
- A straight line has a curvature of 0, because there is no change of the unit tangent vector.
This suggests a geometric definition of curvature...
Osculating circle
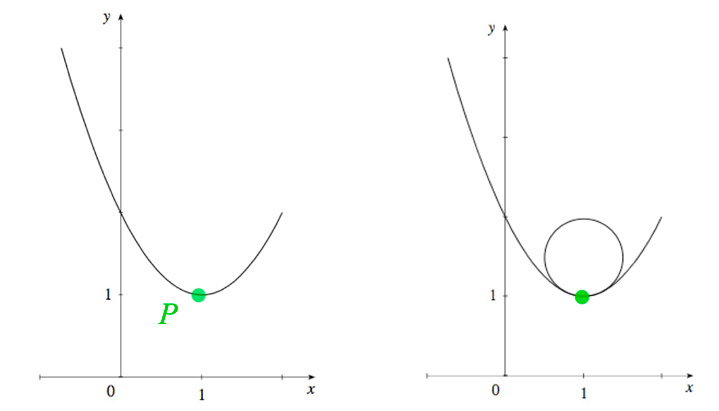
The circle with the same curvature (that is, radius=$1/\kappa$) as $\myv r(t)$ at a point $P$ on the curve.
Another way to calculate curvature
We had: $$\kappa = \left|\frac{d\uv T}{dt}\right| \frac{dt}{ds} = \frac{|d\uv T(t)/dt|}{|\myv r'(t)|} = \frac{\left|\frac{d}{dt}\left[ \frac{\myv r'(t)}{|\myv r'(t)|}\right]\right|}{|\myv r'(t)|}.$$
Theorem: The curvature of the curve given by $\myv r(t)$ is given by: $$ \kappa(t)=\frac{|\myv r'(t)\times \myv r''(t)|}{|\myv r'(t)|^3}.$$
Do 9.8.6 - curvature of an ellipse, part a. Start by graphing the ellipse with $a=1$ and $b=4$. Based on the sketch, where do you think the curvature will be greatest or smallest? (and what values of $t$ locate those points?)
Example 4 - group work
...uses the formula above to calculate the curvature of the 'twisted cubic' $\myv r(t)=\langle t,t^2,t^3 \rangle$: $$\kappa(t)=\frac{2\sqrt{1+9t^2+9t^4}}{(1+4t^2+9t^4)^{3/2}}$$ The twisted cubic...[plot the twisted cubic.]
- Would you expect the curvature function to be symmetric or not about $t=0$ which corresponds to $(0,0,0)$?
- Would you expect there to be a maximum, minimum, or neither at $t=0$?
[Graph $\kappa(t)$ to see...]
Unit tangent, unit normal, binormal
Several quantities, defined in terms of derivatives of $\myv r(t)$:
The unit tangent vector is $$\uv T(t) \equiv \frac {\myv r'(t)}{|\myv r'(t)|}.$$
Under what circumstances is $\uv T'(t)=0$?
(That is to say, $\uv T'\equiv \frac{d}{dt}\uv T$ is not necessarily a unit vector.)
But when $|\uv T'(t)|\neq 0$...
- $\uv T(t)$ is a vector whose length (=1) is not changing with time.
- Therefore $\uv T'(t)$ must be at right angles to ("normal to") $\uv T$.
The unit normal vector is $$\uv N(t) \equiv \frac {\uv T'(t)}{|\uv T'(t)|}.$$
$\uv N$ points towards the center of the osculating circle for $\myv r(t)$.
What's the magnitude of the cross product of two unit vectors, which are at right angles?
The binormal vector is $$\myv B(t)=\uv T(t)\times\uv N(t).$$
We may as well write it as $\uv B(t)$ because it must have unit length by this definition.
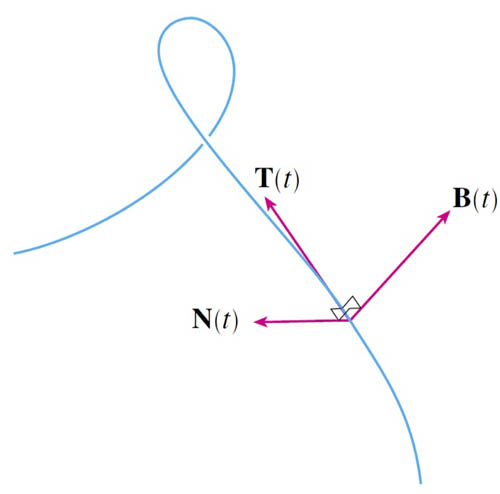
Example
For $\myv r(t)=2\cos t \uv i + 2\sin t \uv j + 3t \uv k$: Find $\uv T$, $\uv N$, and $\uv B$ at $t=3\pi/2$. Sketch these on a plot of $\myv r(t)$.
See 10.3.TBN.nb for calculations
Acceleration- components
Interesting things happen when we resolve acceleration into components parallel (tangential) and perpendicular (normal) to the velocity...
Since the unit tangent vector $\uv T=\frac{\myv r'(t)}{|\myv r'(t)|}=\frac{\myv v}{v}$, $$\myv v= v\uv T.$$
Differentiating both sides of this equation, using the product rule on the right, gives us $$\myv v' = \myv a = v' \uv T + v \uv T'.\label{accel}$$
Now re-writing 2 relations from 10.3 in terms of velocity/speed: The curvature, $\kappa$, $$\nonumber \kappa = \frac{|\uv T'|}{|\myv r'|}= \frac{|\uv T'|}{v},$$ and the unit normal vector $\uv N=\uv T'/|\uv T'|$, $$\nonumber \uv T' = |\uv T'| \uv N=\kappa v \uv N.$$
Substituting into \ref{accel},
$$\myv a = v' \uv T +\kappa v^2 \uv N.$$
- No $\uv B$ component (binormal) to the acceleration??!!
- This means that acceleration is always in the $\uv T$-, $\uv N$-plane.
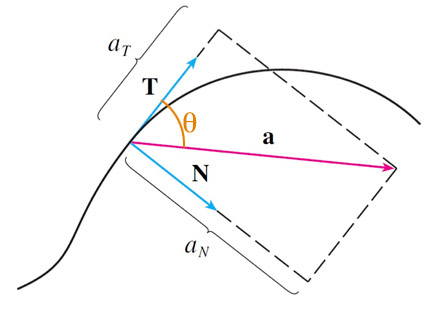A change in speed, $v'$ only affects the tangential component, $a_T$.
- A very important difference from motion in one dimension is the acceleration of the velocity vector due to a change in direction:
If a particle is moving around a curve, even at constant speed, it must have a normal component of acceleration towards the "inside" of the curve (towards the center of the osculating circle).
- The normal component of acceleration, $a_N$, is only sensitive to speed^2 and curvature, not the change in speed.
- Newton's law is: $\myv F = m \myv a$.
- So, the "sideways force" (the normal force) that the rails/road exerts on a train/car in order to keep it on the track/road is the normal component of the force (also called the centripetal force):
$$F_N=ma_N=m\kappa v^2.$$
There is a maximum sideways force that rails can exert before a train "hops the rails"...
[People, > 70, died in this accident :-<]"Twice the speed limit"...
If you double the speed, the sideways force needed to stay on the rails quadruples.
Components in terms of $\myv a$
$$\myv a(t)=a_T(t) \uv T(t)+a_N(t)\uv N(t).$$
[In what follows, I'll stop writing the explicit time dependence, but just remember that all the quantities we're dealing with are time dependent.]
The tangential component, $a_T$ is the dot product of $\myv a$ with a unit vector in the tangential direction, namely $\uv T$: $$\begineq a_T&=\myv a\cdot\uv T\\ &=\myv a \cdot \frac{\myv v}{|\myv v|}=\frac{\myv a\cdot \myv v}{v}.\\ \endeq$$
We can write the dot product as $\myv a \cdot \uv T=a \cos \theta$, where $\theta$ is the angle between $\myv a$ and $\uv T$.
Since $\uv T \perp \uv N$, We could write $$\nonumber a_N=\myv a \cdot \uv N = a \sin \theta.$$
But $|\myv a \times \uv T| = a \sin \theta$ too, so
$$\begineq a_N &= |\myv a \times \uv T| \\ &= \left|\myv a \times \frac{\myv v}{v} \right| = \frac{|\myv a \times \myv v|}{v} .\endeq$$
Summary
Unit tangent vector
$$\uv T = \frac{\myv v}{v}$$
Unit Normal vector
$$\uv N = \frac{\uv T'}{|\uv T'|}$$
Decomposition of acceleration
$$\uv a(t)=a_T(t) \uv T(t) + a_N \uv N(t)$$
Tangential component
$$a_T=v'=\frac{\myv a \cdot \myv v}{v}$$
Normal component
$$a_N=\kappa v^2 =\frac{|\myv a \times \myv v |}{v}$$
$$a_N \uv N=\myv a -a_T\uv T = \myv a - \frac{\myv a \cdot \myv v}{\myv v\cdot\myv v}\myv v$$