Limits and Continuity [10.1]
Sometimes where you end up depends on how you pursue your goals!
Limit definition
$$\lim_{(x,y)\to (a,b)} f(x,y)=L$$ Meaning:
- As $(x,y)$ approaches $(a,b)$...
- the limit of $f(x,y)$ is $L$...
- *if* we can make the value of $f(x,y)$ as close to $L$ as we like...
- by taking $(x,y)$ sufficiently close to the point $(a,b)$, but not equal to $(a,b)$!
Examples
What happens as both $x$ and $y$ approach 0 for the function... $$f(x,y)=\frac{\sin(x^2+y^2)}{x^2+y^2}?$$
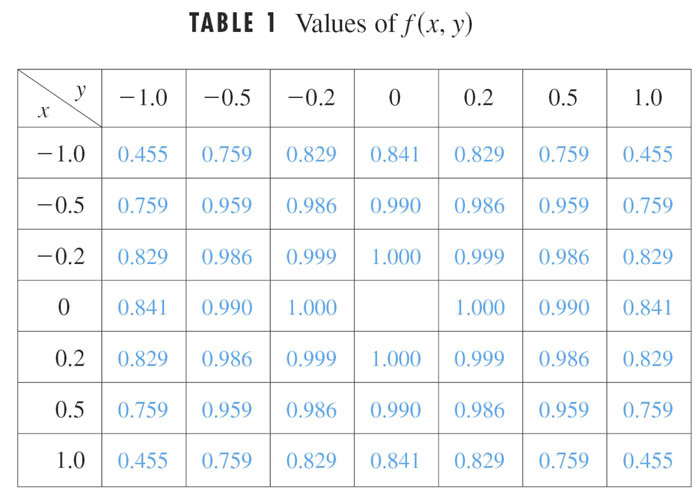
It appears that we can write: $$\lim_{(x,y)\to (0,0)} f(x)= 1.$$
What happens as both $x$ and $y$ approach 0 for the function... $$g(x,y)=\frac{x^2-y^2}{x^2+y^2}?$$
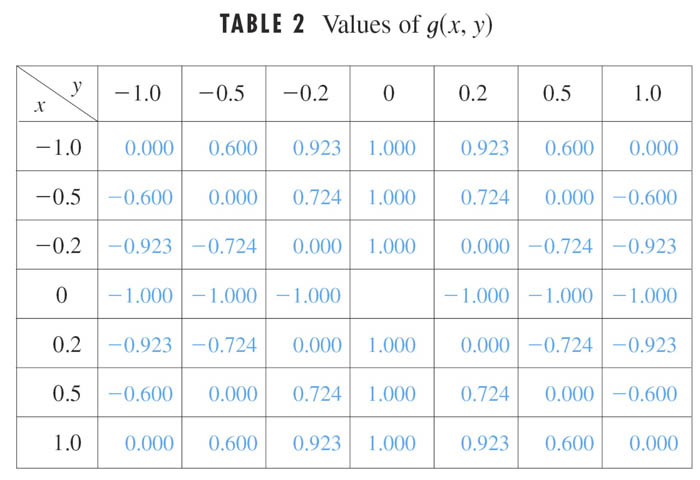
It appears that: $$\lim_{(x,y)\to (0,0)} g(x)\ \text{does not exist}.$$
Graphs of the two function
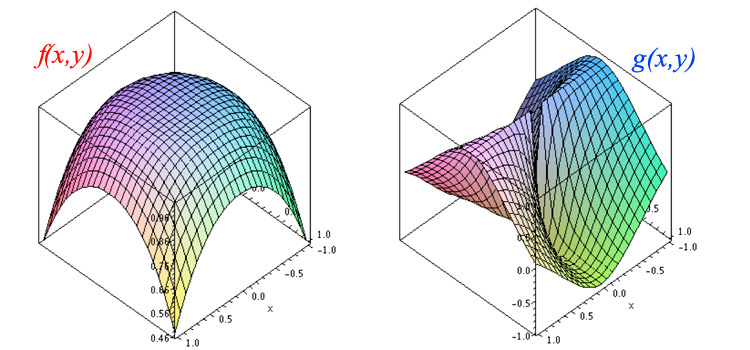
Direction of approach
$$\lim_{(x,y)\to (a,b)} f(x,y)=L$$ means that the values of $f(x, y)$ approach the number $L$ as the point $(x, y)$ approaches the point $(a, b)$ along any path that stays within the domain of $f$:

- Our definition says that the distance between $f(x, y)$ and $L$ can be made arbitrarily small by making the distance from $(x, y)$ to $(a, b)$ sufficiently small (but not 0).
- The definition refers only to the distance between $(x, y)$ and $(a, b)$. It does not refer to the direction of approach.
- Therefore, if the limit exists, then $f(x, y)$ must approach the same limit no matter how $(x, y)$ approaches $(a, b)$.
- Thus, if we can find two different paths of approach along which the function has different limits, then $f(x, y)$ has no limit as $(x, y)$ approaches $(a, b)$.
For the function $g(x)=(x^2-y^2)/(x^2+y^2)$ the particular directions:
- Along the $y$-axis, $x=0$, so $g(x,y)\to -y^2/y^2$, so apparently the limit when approaching the origin will be -1.
- But along the $x$-axis, $y=0$, so $g(x,y)\to x^2/x^2$, so apparently the limit when approaching the origin will be 1.
...So we have two different paths of approach with different limits, and therefore *the* limit of the $g(x,y)$ is not unique near the origin, and does not exist.
Converse?
If we can show the same limit when approaching $(a,b)$ from two different directions, does that mean that a function has a unique limit at $(a,b)$?
Consider the function $h(x,y)$ $$h(x,y)=\frac{xy}{x^2+y^2}.$$ Does it have a limit at the origin $(0,0)$ or not?
- along the $x$-axis: to get to the $x$-axis, $y\to 0$, and when this happens $f(x,y)\to 0/x^2\to 0$.
- along the $y$-axis: to get to the $y$-axis, $x\to 0$, and when this happens $f(x,y)\to 0/y^2\to 0$.
So, same limit from two different directions.
But approaching the origin along the line $x=y\equiv t$: $$h(t,t)=t^2/(2 t^2)\to 1/2.$$ So the limit along this line is 1/2, and *the* limit of $h$ at $(0,0)$ is not unique.
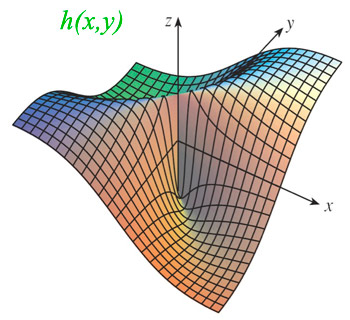
Graphically...
What is the limit as you approach the origin along the line $x=-y$?

Continuity
A function $f$ of two variables is called continuous at $(a,b)$ if $$\lim_{(x,y)\to (a,b)} = f(a,b).$$
We say $f$ is continuous on $D$ if $f$ is continuous at every point $(a,b)$ in $D$.
To do
- 10.1.Limits handout
