Which way to go?

The hiking question(s)

Which direction should I go...
- to go up most steeply?
- to go down most steeply?
- to keep moving around the mountain while staying at the same altitude?
- Also, how steep is the path I'm on right now?
Ummmmm... Actually our brains working with our eyes are pretty good at answering such questions unconsciously with little or no calculus training!
We will instead be trying to answer questions about surfaces for which we have a mathematical description (often a function). The surfaces will mostly be continuous and well behaved.
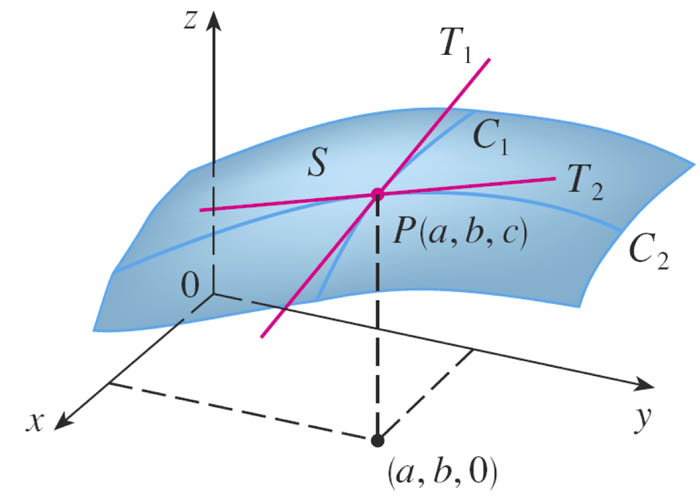
The slope...in any direction

For a function, $f(x)$, of one variable, $\frac{df}{dx}$ is *the* slope of the graph at $x$.
But on a mountain (=surface), slope depends on the direction of motion. Or we could say, it depends on the path taken.
Partial derivatives [10.2]
If $f$ is a function of two variables, then its partial derivatives are the functions $f_x$ and $f_y$ defined by $$f_x(x,y)=\lim_{h\to 0}\frac{f(x+h,y)-f(x,y)}{h}$$ $$f_y(x,y)=\lim_{h\to 0}\frac{f(x,y+h)-f(x,y)}{h}$$ In the first definition, $y$ is constant and $x$ varies. In the second one $x$ is constant and $y$ varies.
Notation... $$f_x(x,y)\equiv f_x\equiv \frac{\del f}{\del x}\equiv \frac{\del}{\del x}f(x,y)\equiv \frac{\del z}{\del x}\equiv D_x f.$$ $$f_y(x,y)\equiv f_y\equiv \frac{\del f}{\del y}\equiv \frac{\del}{\del y}f(x,y)\equiv \frac{\del z}{\del y}\equiv D_y f.$$ with $z=f(x,y)$.
[I have seen $f_1$ or $D_1$ very rarely].
Rules for calculating partial derivatives
- To find $f_x$, regard $y$ as constant, and differentiate $f(x,y)$ with respect to $x$.
- To find $f_y$, regard $x$ as constant, and differentiate $f(x,y)$ with respect to $y$.
For example: $$f(x,y)=3xy^2$$
$$f_x=\frac{\del }{\del x} (3y^2)x=3y^2$$
$$f_y=\frac{\del }{\del y}(3x)y^2=(3x)*2y=6xy$$
 In CoCalc (at right):
In CoCalc (at right):
Mathematica: D[f,x], D[f,y]
Do A 10.2.4, Speed of sound in the ocean.
Visualizing
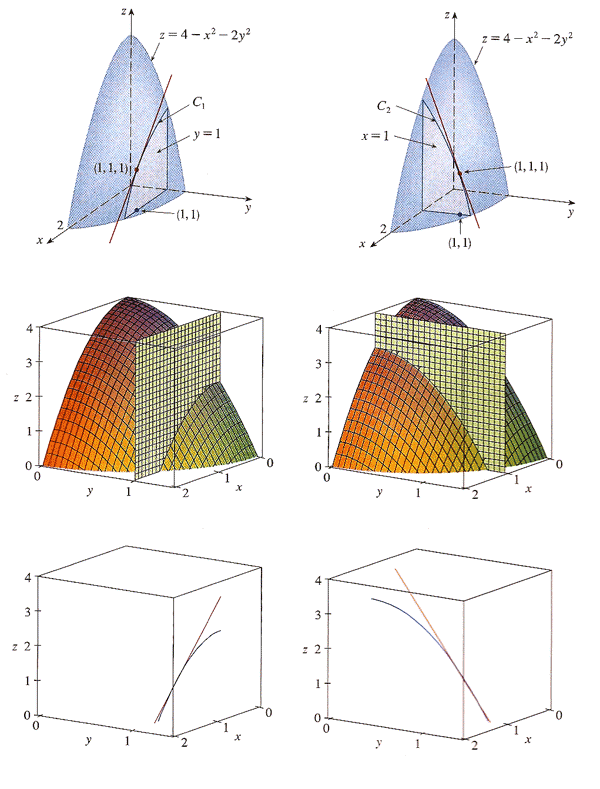
- Tabular data - Just 1-3.
- Graphical data - Just 1-3.