Directional derivatives and the gradient

For a function $f(x,y)$, we have $f_x\equiv$ slope in the $x$-direction, and $f_y\equiv$ slope in the $y$-direction. What if we want the slope in some direction other than just the $x$- or $y$-direction?

Extended example

Consider the function $$\nonumber f(x,y)\equiv z(x,y)=x^2+xy$$

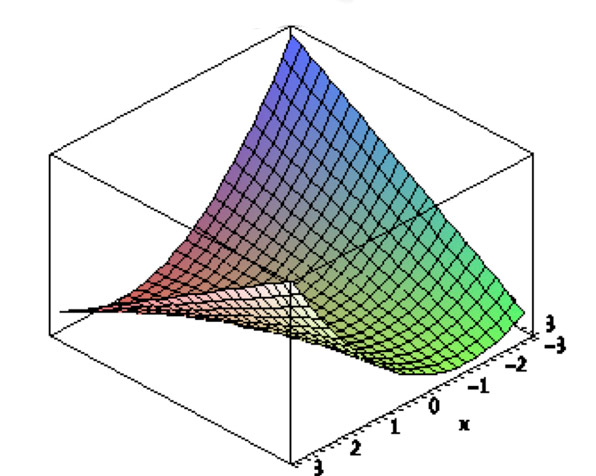
How does the surface height, $z$, vary as you move along the line $$\nonumber x=t;\ \ y=2\ ?$$

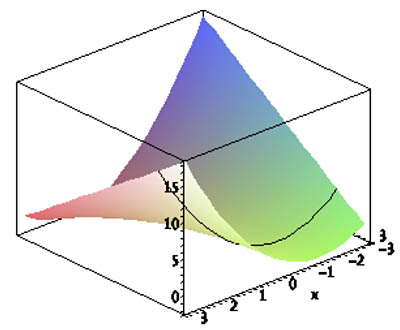
Height $z$ along the line $$\nonumber x=t;\ \ y=2\ ?$$ $$\nonumber \left. \begin{eqnarray*} f(x,y)&= x^2+xy\\ x&=t\\ y&=2 \end{eqnarray*} \right\}\Rightarrow z=t^2+2t$$

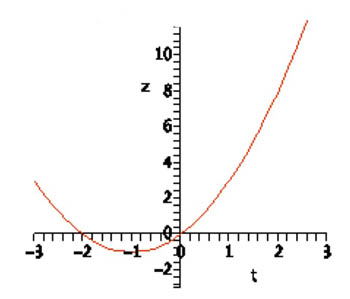
Compare

$$\nonumber \frac{dz}{dt}=2t+2$$

The chain rule...$$ \begineq \frac{dz}{dt} &= \frac{\del z}{\del x} \frac{dx}{dt} + \frac{\del z}{\del y} \frac{dy}{dt}\\ &=[2x+y](1)+[x](0)\\ &=2x+2=2t+2\\ \endeq $$

Height $z$ along the line $$\nonumber x=1;\ \ y=2+t\ ?$$

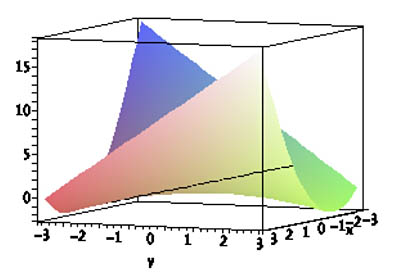
$$ \left. \begin{eqnarray*} f(x,y)&= x^2+xy\\ x&=1\\ y&=2+t \end{eqnarray*} \right\} \Rightarrow z=1^2+(2+t)=3+t $$

Compare

$$\nonumber \frac{dz}{dt}=1$$

The chain rule...$$\nonumber \begineq \frac{dz}{dt} &= \frac{\del z}{\del x} \frac{dx}{dt} + \frac{\del z}{\del y} \frac{dy}{dt}\\ &= [2x+y](0)+[x](1)= \left. x\right|^{x=1}=1 \endeq $$

Height $z$ along the line $$\nonumber x=-3+t;\ \ y=-3+t\ ?$$ $t=0\Rightarrow (x,y)=(-3,-3)$ $t=6\Rightarrow (x,y)=(3,3)$

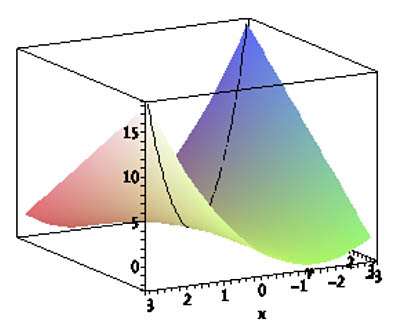
$$ \left. \begin{eqnarray*} f(x,y)&= x^2+xy\\ x&=-3+t\\ y&=-3+t \end{eqnarray*} \right\} $$ $$ \begineq \Rightarrow z&= (-3+t)^2+(-3+t)(-3+t)\\&=2(-3+t)^2 \endeq $$

Compare

$$\nonumber \frac{dz}{dt}=4(-3+t)=4t-12$$

The chain rule...$$\nonumber \begineq \frac{dz}{dt} &= \frac{\del z}{\del x} \frac{dx}{dt} + \frac{\del z}{\del y} \frac{dy}{dt}\\ &=[2x+y](1)+[x](1)=3x+y\\ &=3(-3+t)+(-3+t)=4t-12 \endeq $$

Height $z$ along the line $$\nonumber x=-3+t;\ \ y=3-t\ ?$$ $t=0\Rightarrow (x,y)=(-3,3)$ $t=6\Rightarrow (x,y)=(3,-3)$

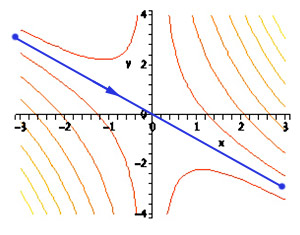
$$\nonumber \left. \begin{eqnarray} f(x,y)&= x^2+xy\\ x&=-3+t\\ y&=3-t \end{eqnarray} \right\} $$ $$ \begineq \Rightarrow z&=(-3+t)^2+(3-t)(-3+t)\\ &=(-3+t)^2-(-3+t)^2=0\endeq$$

Compare

$$\nonumber \frac{dz}{dt}=0$$

The chain rule...$$\nonumber \begineq \frac{dz}{dt} &= \frac{\del z}{\del x} \frac{dx}{dt} + \frac{\del z}{\del y} \frac{dy}{dt}\\ &=[2x+y](1)+[x](-1)=x+y\\ &=(3-t)+(-3+t)=0\\ \endeq $$

So, by parameterizing a direction with $t$, we can evaluate the slope along any direction.

But usually we think of $t$ as time, so the units of our slopes will be $$\frac{\Delta z}{\Delta t} =\left[m/sec\right].$$ We should like to have the same units as a traditional slope, where both $\Delta z$ is in meters (the "rise") and denominator is the "run", in meters...

Derivative in some arbitrary direction

Let's say that we want the slope of the surface $z(x,y)$ in some arbitrary direction. Can we use the machinery that we used above--the chain rule and a line in the $x$- $y$-plane, but parameterized in terms of the distance along such a line, $h$, instead of the time?

Yes:

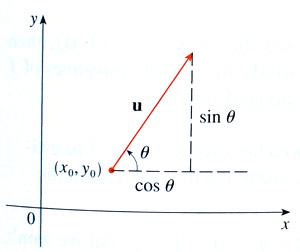Let's say that the direction in the $x$- $y$-plane is specified by a unit vector $\uv u$. In terms of the angle $\theta$ that it makes with the $x$-axis, its components are $$\uv u = \langle \uv u \cdot \uv i, \uv u \cdot \uv j\rangle=\langle \cos \theta, \sin \theta \rangle \equiv \langle u_1,u_2 \rangle.$$

A vector function for the line $L$ running through $(x_0,y_0)$ which is parallel to the direction vector $\uv u$ in terms of a parameter $h$ is $$\begineq\langle x(h), y(h)\rangle &= \myc{ x_0,y_0}+h\myc{ u_1, u_2 }\\ &= \langle x_0+hu_1, y_0+hu_2 \rangle.\endeq$$ And by construction, $h$ is now the length (say in meters) along the line from the point $(x_0,y_0)$.

Your book defines the directional directive of the function/surface $f(x,y)\equiv z$ at a particular point:

The directional derivative of $f$ at $(x_0,y_0)$ in the direction of a unit vector $\uv u=\langle a, b\rangle$ is $$D_{\uv u} f(x_0,y_0) \equiv \lim_{h \to 0} \frac{f(x_0+hu_1,y_0+hu_2)-f(x_0,y_0)}{h}.$$

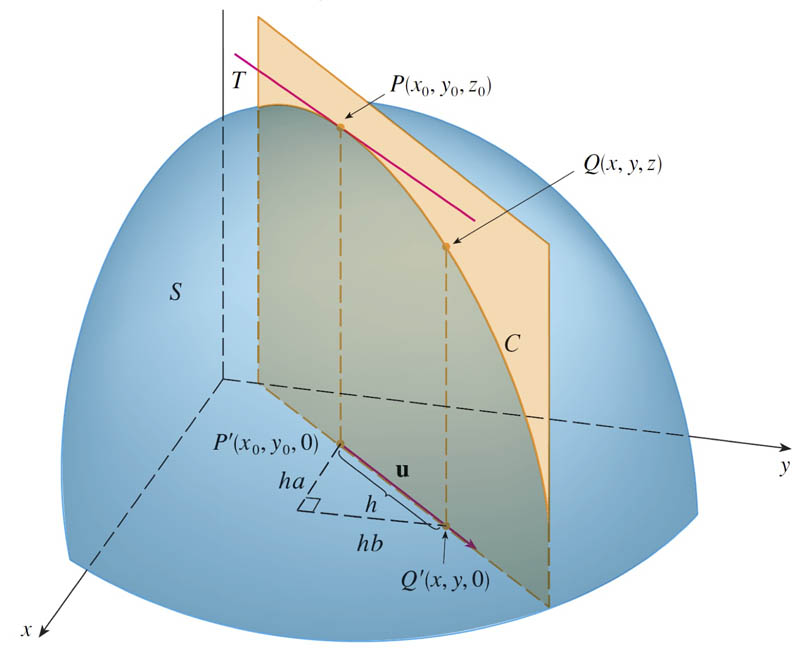
But we are in a position to find a slightly more general version, using the chain rule: $$\begineq D_{\uv u}z(x,y)&=\left. \frac{dz}{dh}\right|^{\text{along }L}\\ &= f_x \left. \frac{dx}{dh}\right|^{\text{along }L} + f_y \left. \frac{dy}{dh}\right|^{\text{along }L}\\ &=f_x a + f_y b &=\frac{\del f}{\del x} u_1 + \frac{\del f}{\del y} u_2 \endeq$$

Since $\uv u=u_1 \uv i + u_2\uv j$ we could formally write this as a dot product of two vectors: $$D_{\uv u}f = \langle f_x,f_y \rangle \cdot \uv u\label{protog}.$$ That quantity in $\langle ... \rangle$ is so useful that we give it a name:

The gradient

If $f$ is a function of $x$ and $y$, then the gradient of $f$ is the vector function defined by $$ \myv \grad f \equiv \langle f_x(x,y),f_y(x,y) \rangle = \frac{\del f}{\del x} \uv i + \frac{\del f}{\del y}\uv j.$$

With this definition, the directional derivative can be written $$D_{\uv u} f = \myv \grad f (x,y) \cdot \uv u.$$

Maximizing $D_{\uv u}$