Maximum and Minimum Values

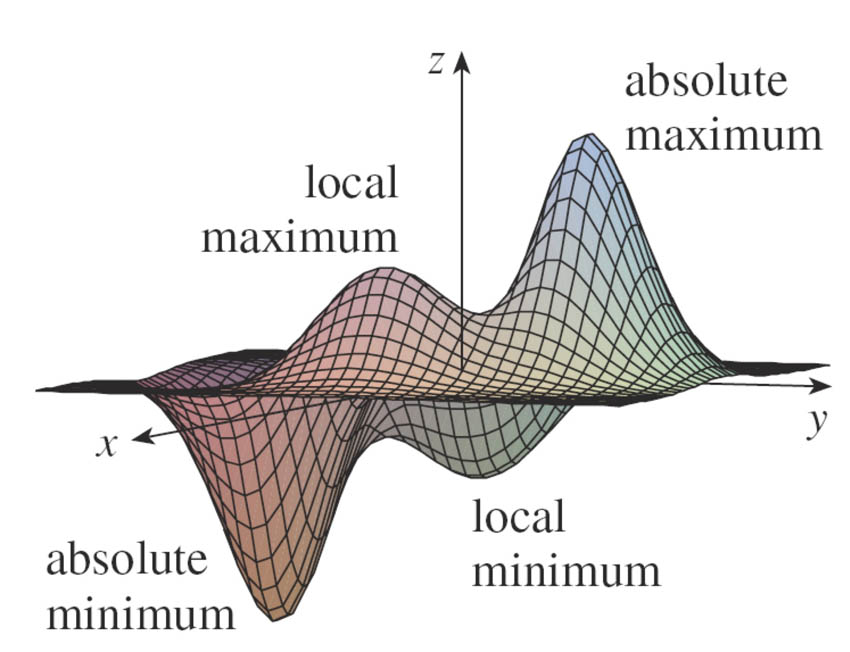
A definition and a theorem

A function of two variables has a local maximum at $(a,b)$...

• if $f(x,y)\leq f(a,b)$ when $(x,y)$ is near $(a,b)$.
• [This means that $f(x,y)\leq f(a,b)$ for all points $(x,y)$ on some disk centered at $(a,b)$.]
• The number $f(a,b)$ is called the local maximum value

...if instead $f(x,y)\geq f(a,b)$ near $(a,b)$, then $f(a,b)$ is a local minimum value.

Theorem if $f$ has a local maximum (or minimum) at $(a,b)$, and the first order partial derivatives exist there, then $$f_x(a,b)=0 \ \ \text{ and }\ \ f_y(a,b)=0.$$

Does this relationship go the other way?

Consider the saddle point pictured...

Second derivatives test

In calculus of one variable, the second derivative can be used to decide if a point is a maximum, minimum, or neither. There's a second derivatives test for functions of two variables:

Suppose that the first partial derivatives exist, and vanish at $(a,b)$, that is $f_x(a,b)=f_y(a,b)=0$, then $(a,b)$ is a critical point.

Now, suppose that in addition, the second partial derivatives of $f$ also exist on a disk centered at $(a,b)$. The determinant of the Hessian matrix of 2nd derivatives, $D$, turns out to be useful for testing critical points: $$\begineq D(a,b)&\equiv f_{xx}(a,b)f_{yy}(a,b)-\left[f_{xy}(a,b)\right]^2\\ &=\text{det} \begincv f_{xx} & f_{xy}\\ f_{yx} & f_{yy} \endcv \endeq $$

(*) Either $f_{xx}(a,b)$ or $f_{yy}(a,b)$ can be tested..

Do A 10.7.4 - Find and classify the critical points.

Example

Find three positive numbers whose sum is $n$, and whose product is a maximum.

We could define these two conditions as: $$x+y+z=n$$ and $$xyz=\text{maximum}.$$

One approach

1. Solve the first equation for $z$: $$z=n-x-y$$
2. Define the product of the three numbers as a function of $x$ and $y$, by subbing in for $z$: $$f(x,y)=xy(n-x-y)=nxy-x^2y-xy^2.$$
3. The maximum of this function will occur when both $\frac{\del f}{\del x}=0$, and $\frac{\del f}{\del y}=0$.
4. This is two equations and there are two unknowns, $x$ and $y$. Solve the two equations for $x$ and $y$.
5. Actually there is more than one $(x,y)$ pair that solves this, but you can try them out, and see which gives the largest product. (Hint, some of them involve $x=0$ or $y=0$, which will give a minimum for the product, instead of a maximum).

Bounded regions

• The Extreme Value Theorem claims that
  1. there is always an absolute maximum and an absolute minimum...
  2. for some points in a closed and bounded region
  3. of a continuous function, $f(x,y)$.

  The points could be in the interior, or on the boundary.

  To check the boundary, parameterize it, in segments if necessary, and check for critical points on the boundary, or at the endpoints of the boundaries.

  Do 10.7.6 - a triangular domain

  A quick way to view the bounded domain in GeoGebra is the plot the surface, and then the three planes, $x=0$, $y=0$, $y=-x$.