Lagrange multipliers [10.8]
How to find peaks, or valleys, along a particular path?
1st approach
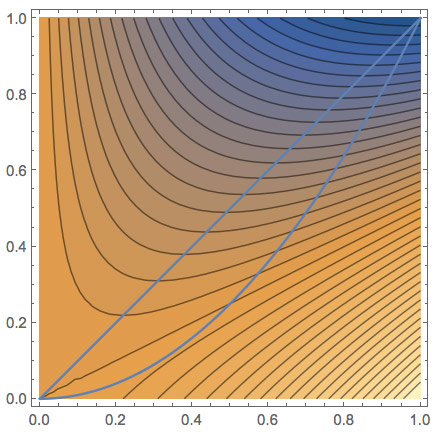
In the kitten problem, $T(x,y)=x^2-2xy$, you guessed that the highest temperature occurred on the bottom blue boundary, as close to the next-highest contour line outside as possible.
Now we'll carry out two try approaches (which will hopefully agree!)::
- Parameterize the blue path, $y=x^2$, coming up with $x(t)$ and $y(t)$,
- Find $z(t)=T(x,y)=T(x(t),y(t))$
- Find critical points: $t$ such that $dz/dt=0$. If more than one, figure out the maxima.
- Use that $t$ to find coordinates $x(t)$ and $y(t)$.
What are the coordinates of the point along the boundary with the highest temperature?
Now we'll try a another way, a new one...
The gradient and contour lines
$z=f(x,y)$ is the equation for a surface in three dimensions.
What we mean by a "contour line":
- $f(x,y)=k$ is a level curve or contour line.
- A contour line is a curve graphed in the $xy$ plane. (Not in 3-dimensions.)
The gradient at a point $(x_0,y_0)$ in the $xy$ plane:
- $$\begineq \myv \grad f(x_0,y_0)&=f_x(x_0,y_0)\uv i +f_y(x_0,y_0)\uv j\\ &\equiv\left.\frac{\del f(x,y)}{\del x}\right|^{(x_0,y_0)} \uv i +\left.\frac{\del f(x,y)}{\del y}\right|^{(x_0,y_0)} \uv j \endeq$$
- It points in the direction of maximum slope of the surface $z=f(x,y)$.
- But the gradient is a vector in the $xy$ plane. (It has no $z$ component).
- The gradient at $(x_0,y_0)$ is always perpendicular to the contour line $f(x,y)=k=f(x_0,y_0)$.
At every point along the 2-d curve $f(x,y)=k$, the gradient $\myv \grad f$ is a normal vector of the curve.
Using gradients to find extreme points
Imagine that you are hiking along a path specified by the equation $g(x,y)=k$ through a landscape where the height is specified by $f(x,y)$. How do you find the highest point of your hike?
In mathematical terms:
- Try to find the extreme values of $f(x,y)$...
- Subject to the constraint $g(x,y)=k$.
We seek the the extreme values of $f(x,y)$ when the point $(x,y)$ is restricted to lie on the level curve $g(x,y)=k$.
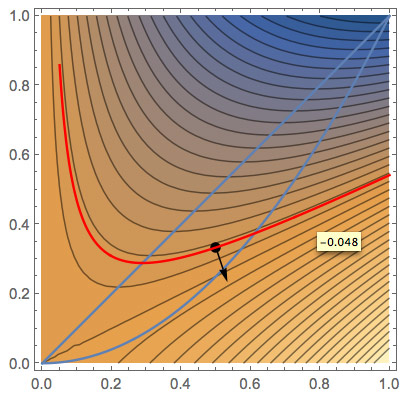
E.g. maximizing $f(x,y)$ means finding the contour $f(x,y)=c$ that $g(x,y)$ touches, where $c$ has the largest possible value.
It looks like this happens when the desired contour of $f$ is tangent to $g(x,y)=k$.
[If $g$ is not tangent to a particular contour of $f$, then there exists a point on $g$ which is higher, and one which is lower on either side of their intersection.]
Tangent means that the normal vectors to the 2-d curves $g=k$ and $f=c$ are parallel (one is the scalar multiple of the other).
We know $\myv \grad f$ is always normal to any 2-d contour line of $f$. Ditto for $\myv \grad g$ along the particular contour line $g=k$. Therefore...
At the location $(x_0,y_0)$ where the two contours are tangent, it will also be the case that the normals are parallel, $\myv \grad f \parallel \myv \grad g$, which means: $$\myv \grad f(x_0,y_0) = \lambda \myv \grad g(x_0,y_0)$$ where $\lambda$ is some scalar.
The method of Lagrange multipliers
Kitten, re-re-visited
$$T(x,y)=x^2-2xy$$ The gradient of this function.. $$\myv\grad T= T_x\uv i + T_y\uv j= (2x-2y)\uv i -2x\uv j.$$
We're interested in the the highest contour of $T$ along the path $y=x^2$.
We need to express the path $y=x^2$ in the form of $g(x,y)=k$... How about
$$g(x,y)=x^2-y=0?$$
We can calculate the gradient of this function... $$\myv\grad g=2x \uv i -1\uv j.$$
The condition that the gradients are parallel, $$\begineq \myv \grad T &= \lambda \myv \grad g \\ (2x-2y)\uv i -2x\uv j&= \lambda( 2x \uv i -1\uv j) \\ (2x-2y)\uv i -2x\uv j&= \lambda2x \uv i -\lambda\uv j \\ \endeq$$
Two vectors are only equal if, separately, their $x$ components are equal and their $y$ components are equal.
The $x$-components are equal: $$2x-2y=\lambda 2x$$ and the $y$-components are equal: $$-2x = -\lambda.$$
Using the two to eliminate the scalar $\lambda$: $$2x-2y=(2x)2x=4x^2$$ Taking into account our constraint equation, that $y=x^2$, leads to one equation for $x$: $$\begineq 2x-2(x^2)&=4x^2\\ 1-x&=2x \endeq$$ The solution is $x=1/3$, $\Rightarrow y=1/9$. Hopefully the same location we found by parametric means?!
Solve ing simultaneous equations in Cocalc
[or in Mathematica
Do A 10.8.2 - the cylindrical pop can.
We're trying to minimize the surface area: $$S(r,h)=2\pi r^2+2\pi rh$$
Subject to the constraint that the total volume is $$V=355\text{ cm^3}=\pi r^2 h.$$ We set the gradient of $S$ equal to a scalar multiple of the gradient of V: $$\begineq \myv \grad S &= \lambda \grad V\\ \langle S_r,S_h\rangle &=\lambda \langle V_r,V_h\rangle\\ \langle 4\pi r+2\pi h,2\pi r\rangle &= \langle \lambda 2rh\pi,\lambda \pi r^2\rangle \endeq $$
The three equations to solve for $r$,$h$, and $\lambda$ are:
$$4\pi r+2\pi h = \lambda 2rh\pi;$$
$$2\pi r =\lambda \pi r^2;$$
$$355 =\pi r^2 h.$$
Solving these in CoCalc, and evaluating the only non-imaginary solution:
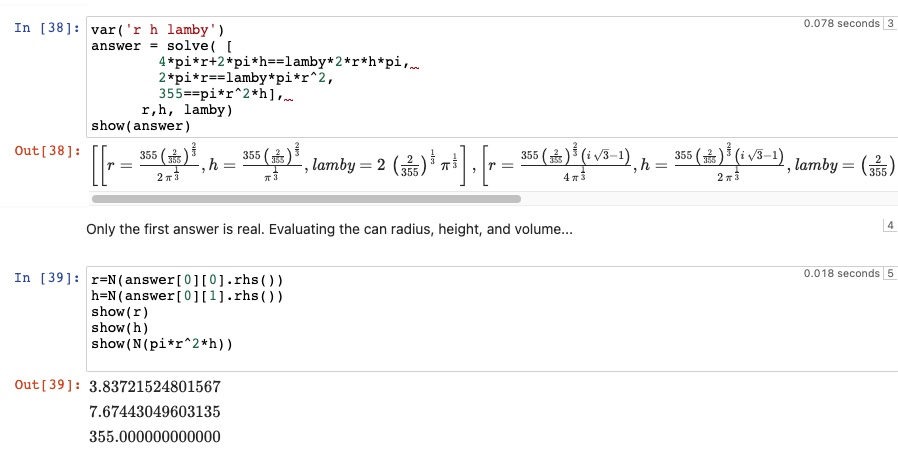
$r=3.84$ cm, $h=7.67$ cm, and I've checked that the volume is 355 cm^3.
Measuring an actual 355 ml can of pop, I found $r=$3.1 cm and $h=$12 cm. The seam on the top of the can, and the rim of the bottom stick out below the cylindrical contents, and the cost of making the ridge probably tilts the real-life calculation towards a relatively smaller radius / height ratio.
Two constraints?
Suppose that we want to find...
- the maximum or minimum values of a function $f(x,y,z)$,
- subject to two constraints: $h(x,y,z)=c$ and $g(x,y,z)=k$.
Geometrically, we are looking for the extreme values of $f$ when $(x,y,z)$ lies on the curve of intersection, $C$, of the level surfaces
$h(x,y,z)=c$ and $g(x,y,z)=k$. Which can be expressed as...
$$\myv\grad f(x_0,y_0,z_0) = \lambda\myv\grad g(x_0,y_0,z_0) + \mu\myv\grad h(x_0,y_0,z_0)$$
where $\lambda$ and $\mu$ are scalars.
This amounts to solving these five equations... $$f_x=\lambda g_x +\mu h_x$$ $$f_y=\lambda g_y +\mu h_y$$ $$f_z=\lambda g_z +\mu h_z$$ $$g(x,y,z)=k$$ $$h(x,y,z)=c$$ for the five unknown quantities $\lambda$, $\mu$, $x$, $y$, and $z$.
ToDo
- Lagrange Multiplier Problems: *Do* use CoCalc to solve the systems of equations.
- ANSWERS (*.pdf file) to the Lagrange Multipliers Problems.