Double integrals over rectangles [11.1]
Approximating volumes with stacks of blocks...
Finding volumes using double integrals
Consider the volume, $V$, of the solid which is...

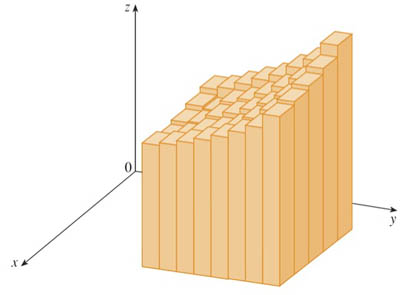
- bounded below by the rectangle, $R=[a,b]\times[c,d]$ in the $xy$ plane,
- Goes straight up from $R$,
- Is bounded above by the surface, $f(x,y)$.
- Split up $[a,b]$ into $m$ sub-intervals, split up $[c,d]$ into $n$ sub-intervals.
Approximate volume is $$V\approx\sum_{i=1}^m\sum_{j=1}^n f(x_{ij}^*,y_{ij}^*)\Delta A.$$ where...
- $(x_{ij}^*,y_{ij}^*)$ is the coordinate of some point in rectangle $R_{ij}$;
- $\Delta A$ is the area of one of the small, identical rectangles with sides $\Delta x=(b-a)/m$ and $\Delta y=(d-c)/n$. That is to say...
$$\Delta A = \left(\frac{b-a}{m}\right)\left(\frac{d-c}{n}\right)=\frac{A}{mn},$$
where $A=(b-a)(d-c)$ is the area of the large rectangular region $R$.
In the limit $\Delta A \to dA \to 0$ this sum becomes exactly this integral $$V=\iint_R f(x,y)dA.$$
To do /handouts/
- mv11.1.data - Double Integrals from Data
$\langle f(x,y) \rangle$ above a rectangular region
Average value of a 1-dimensional function on the interval $[a,b]$: $$\begineq \langle f(x)\rangle&= \frac{1}{b-a}\int_a^b f(x)\,dx\\ &=\frac{1}{l}\int_a^b f(x)\,dx \endeq$$
If you chopped off all the area in the peaks above this line at $y=\langle f(x)\rangle$, it would just fill in the area in the valleys below the line...

Analogously, for a function of $x$ and $y$... $$\begineq\langle f(x,y)\rangle &= \frac{1}{(b-a)(d-c)}\int_a^b\int_c^d f(x,y)\,dy\,dx\\ &= \frac{1}{A}\int_a^b\int_c^d f(x,y)\,dy\,dx.\endeq$$
If you chopped off all the volume in the peaks above this plane surface at $z=\langle f(x,y) \rangle$, it would just fill in the volume of the valleys below this plane.

Approximating the average by sampling
$$\begineq\langle f(x,y)\rangle &= \frac{1}{A}\int_a^b\int_c^d f(x,y)\,dy\,dx\\ &= \frac{1}{A}\sum_i^m\sum_j^n f(x_{ij}*,y_{ij}^*)\Delta A = \frac{\Delta A}{A}\sum_i^m\sum_j^n f(x_{ij}*,y_{ij}^*)\\ &= \frac{\Delta A*m*n}{A}\frac{\sum_{i=1}^m\sum_{j=1}^n f(x_{ij}*,y_{ij}^*)}{m*n}\\ &= \frac{\sum_i^m\sum_j^n f(x_{ij}*,y_{ij}^*)}{m*n},\\ \endeq$$ because there are $m*n$ sub-rectangles, so $A=\Delta A*m*n$. Therefore the average value $\langle f(x,y)\rangle$ is just the average of the sampled values of the function--one sample for each sub-rectangle.To do /handouts/
- mv11.1.park: Back to the Park
Image credits