Parametric surfaces [11.6]

Walt Disney concert hall, Los Angeles, architect: Frank Gehry
- Alternate ways to describe a surface,
- In high symmetry situations, a different parameterization may be simpler (than Cartesian coordinates!)
- Eventually we'd like to answer questions like "how much aluminum will we need for that concert hall roof?".
A vector function $\myv r(t)=\myc{f(t),g(t),h(t)}$ of a single parameter described a curve (quasi-1d object) in space.
A surface is a quasi-2d object. So we'll use two parameters to parameterize such an object.
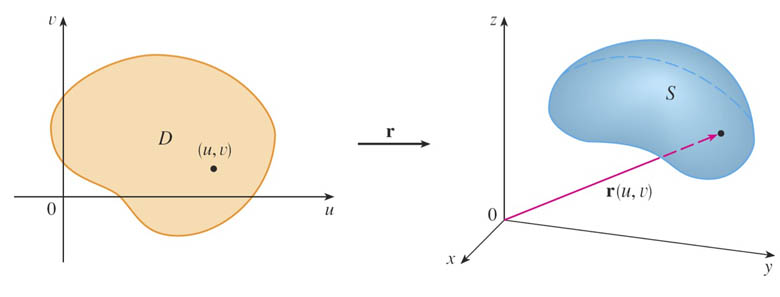
- Suppose that $$\nonumber \myv r(u,v)=\langle x(u,v), y(u,v), z(u,v) \rangle$$ is a vector-valued function,
- Defined on a region $D$ of the $u$- $v$-plane. (parameter space)
- As $(u,v)$ varies throughout $D$, then $\myv r$ traces out a surface $S$ in 3 dimensions.
$x$ and $y$ as 'parameters'
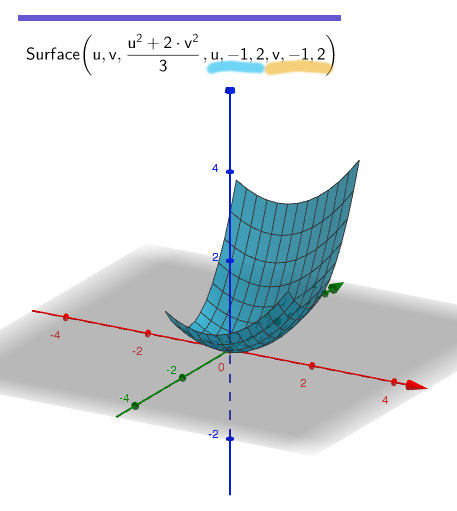
Plot the surface defined by $$z=\frac{x^2+2y^2}3.$$
For our two parameters, we could just use $u=x$, $v=y$, and then $z=\frac{u^2+2v^2}3.$
Turning this into a vector function of $u$ and $v$: $$\myv r=\langle u, v, (u^2+2v^2)/3 \rangle$$
Try copying this code into GeoGebra to reproduce the surface below...
Surface(u,v,(u^2+2*v^2)/3,u,-1,2,v,-1,2)
What happens if you change the numbers (ranges) after u and v in the code above?
Example: plane
$$\myv r(u,v)=\myv r_0 + u\myv a+v\myv b$$
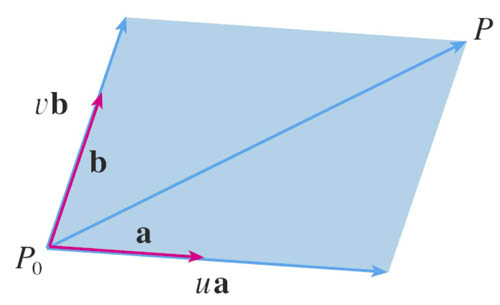
Using $\myv r_0=\myc{0,0,3}$, $\myv a=\myc{1,0,0}$, and $\myv b=\myc{1,1,1}$, figure out how to code a Surface(....) function in Geogebra for a partial plane, such that the parameters run like this: $-1\lt u \lt 3$ and $-1\lt v \lt 4$.
Example: cylinder
$$\myv r(u,v)=\langle 2\cos u, v, 2\sin u \rangle$$
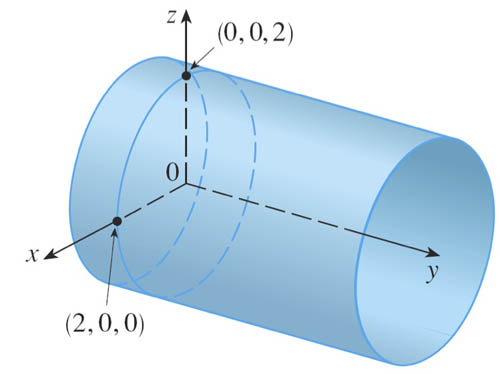
It is also common to have one or more of the parameters representing some angle.
Render in Geogebra the cylindrical surface ab for $-1\lt v\lt 3$. Figure out what the starting and ending value of $u$ should be in order to produce the cylinder.
A spherical surface
Do A 11.6.2 - Make the surface of a sphere
a. Let $s$ be an angle, such that $\frac{-\pi}2 \lt s \lt \frac{\pi}2$. Let $R=2$. Find $x(s)$ and $z(s)$, and code those into GeoGebra (replace the functions below) so as to create the half-circle in the $x$-$z$ plane
Surface( [x(s)], 0, [z(s)], s, -pi/2, pi/2)
b. Yes, think about the radius (distance from the $z$ axis) of a point as you rotate one of the points in your half-circle about the $z$-axis. Think about how to write coordinates $x(t)$ and $y(t)$ in terms of a circle of this radius.
c. Eventually you'll have a cell in GeoGebra that looks like
Surface( [x(s,t)], [y(s,t)], [z(s,t)], s, -pi/2, pi/2, t, [tmin], [tmax] )
Choosing parameters based on symmetries/forms
Consider the points that fulfill: $$\frac{x^2}{4}+y^2+\frac{z^2}{4} = 1$$
You could solve for $z$: $$z=\pm\sqrt{4\left( 1-\frac{x^2}{4}-y^2 \right)} $$ and plot $\myc{x, y, z(x,y)}$.
Or, we re-arrange the equation into $$x^2+z^2 = 4(1-y^2).$$ We recognize the left side as the equation for a circle with a radius $\sqrt{4(1-y^2)}$ that depends on $y$.
This suggests that we write the *radius* as one of the parameters, $u=2\sqrt{1-y^2}$ (and inverting: $y=\sqrt{1-\frac14 u^2}$), and then we could write $x$ and $y$ in terms of a "polar angle" parameter $v$ sweeping around a circle of radius $u$ like this: $$\myv r(u,v)=\myc{u\cos v,\sqrt{1-\frac14u^2},u\sin v}$$