Triple Integrals [11.7]
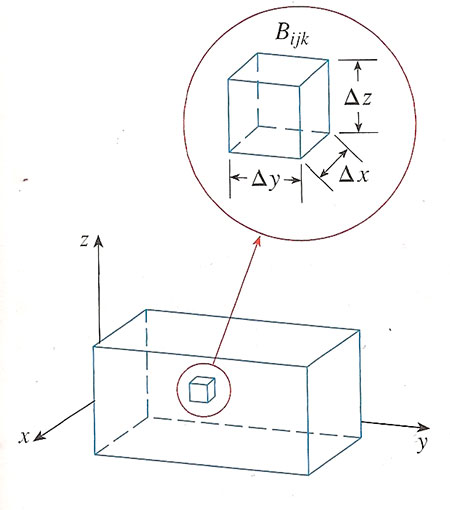
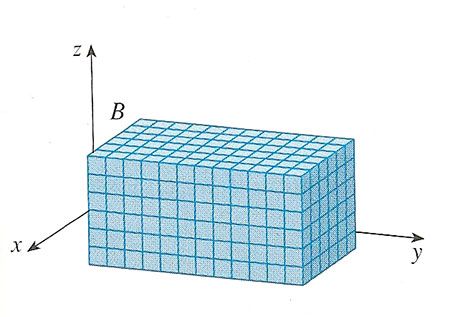
Dividing a box, $B$...
- $l$ equal slices $\perp$ to $\uv i$,
- $m$ equal slices $\perp$ to $\uv j$,
- $n$ equal slices $\perp$ to $\uv k$,
The volume of one little block is $$\Delta V = \Delta x \Delta y \Delta z.$$
And we can evaluate a triple integral by successive iterated integrals.
Order doesn't matter for a box integral, but one possibility is...
- Evaluate... $$A(y,z)=\int_a^b f(x,y,z)\,dx$$ while treating $y$ and $z$ as constants,
- $$B(z)=\int_c^d A(y,z)\,dy$$ while treating $z$ as constant,
- $$\iiint_Bf(x,y,z)\,dV=\int_r^s B(z)\,dz.$$
Integrating over a general bounded region, $E$
$u_1(x,y)$ and $u_2(x,y)$ are surfaces.
$h_1(y)$ and $h_2(y)$ are curves / arcs in the $xy$ plane.
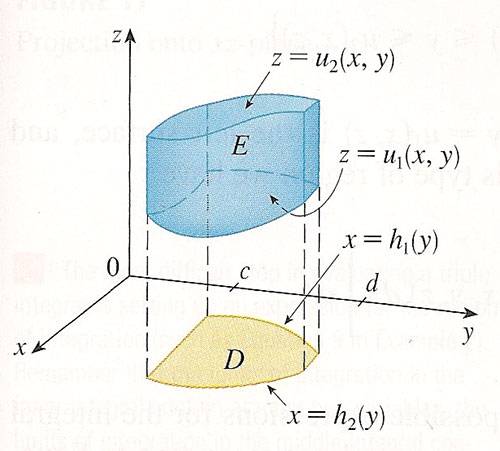Extend the idea of manipulating the limits of the integrals to set up triple integrals over some general bounded 3D region, $E$, whose boundaries can be described in functional form, e.g.
$$\iiint_Ef(x,y,z)\,dV=
\int_{y=c}^d\int_{x=h_1(y)}^{h_2(y)} \int_{z=u_1(x,y)}^{u_2(x,y)}f(x,y,z)\,dz\,dx\,dy.$$
Now the order of evaluating integrals (from inside to outside) does matter.
To find the volume of the solid, $E$, defined by these limits: $$V_E= \int_{y=c}^d\int_{x=h_1(y)}^{h_2(y)} \int_{z=u_1(x,y)}^{u_2(x,y)}\,dz\,dx\,dy$$ where $dx\,dy\,dz=dV$.
To Do
- 11.7 Volume problems