Triple Integrals in cylindrical and spherical coordinates [11.8]
Cylindrical coordinates
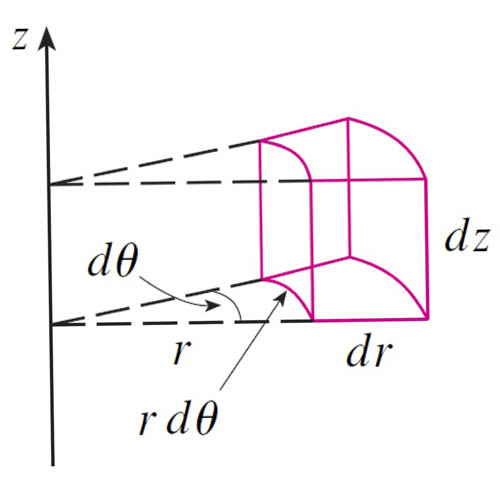The figure shown is very approximately a "box" with volume
$$dV=(r\,d\theta)(dr)(dz)=r\,dr\,d\theta\,dz.$$
Spherical Polar coordinates
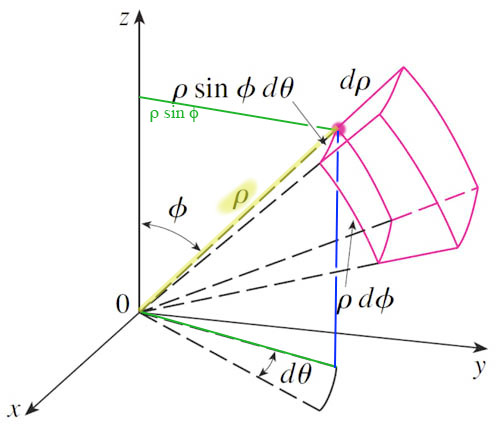
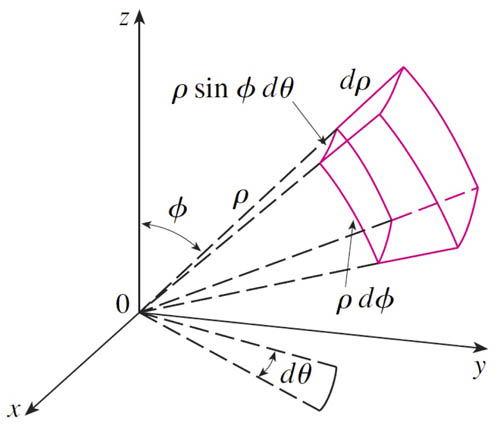The figure shown is very approximately a "box" with volume
$$dV=(\rho\,d\phi)(\rho\sin\phi\,d\theta)(d\rho)=\rho^2\sin\phi\,d\rho\,d\theta\,d\phi.$$
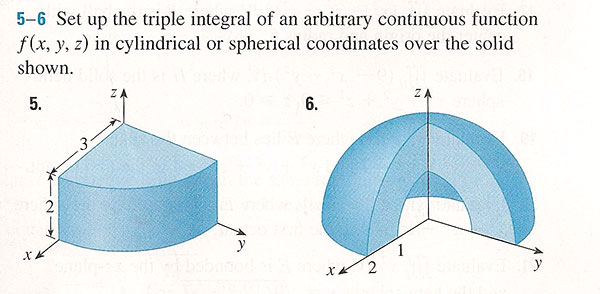
Setting up volume integrals
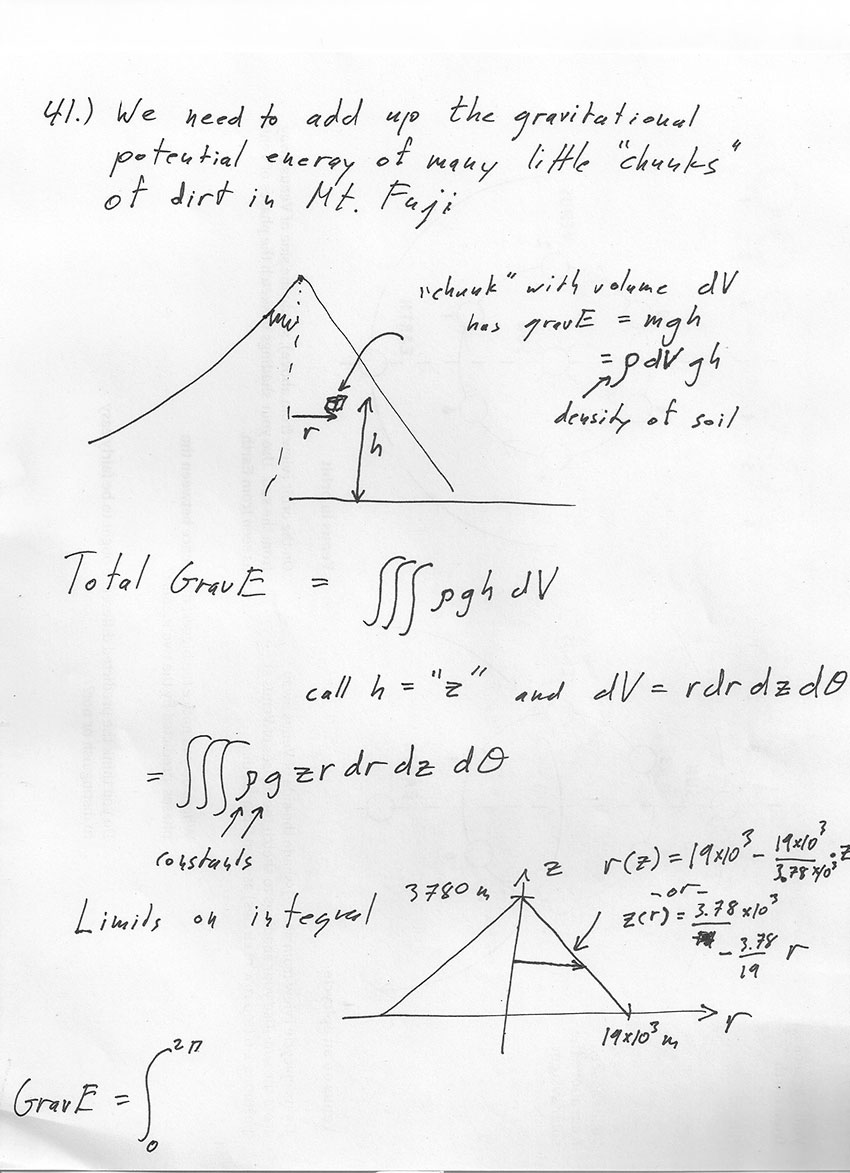
Raising Mt Fuji!
Problem 41. Total work (energy) needed to create Mt Fuji ~Right circular cone with...
- Radius of bottom=62,000 ft ~ 19 km=19,000m.
- Height of 12,400ft=3780m.
- Rock has an average density of $\rho=$200 lbs/ft^3 = 3,200 kg/m^3. (Sorry folks, $rho$ is also the typical symbol used for density! This $rho=3200$ kg/m^3 is not the spherical-polar distance from the origin!!!
- Force of gravity (weight)=$mg$, where $m$ is mass (kg) and $g\approx 10$ m/s^2.
- Energy to lift a mass: The work (energy) $W$ need to lift a mass $m$ through a height difference $h$ is $$W=mgh.$$ if height has units of meters, $g\approx 10$ m/s^2, and $m$ is in kilograms, then $mgh$ will have units of Joules.
It may be easiest to set up the integral as if you were only interested in the volume of Mt Fuji first, and then add the energy after that.
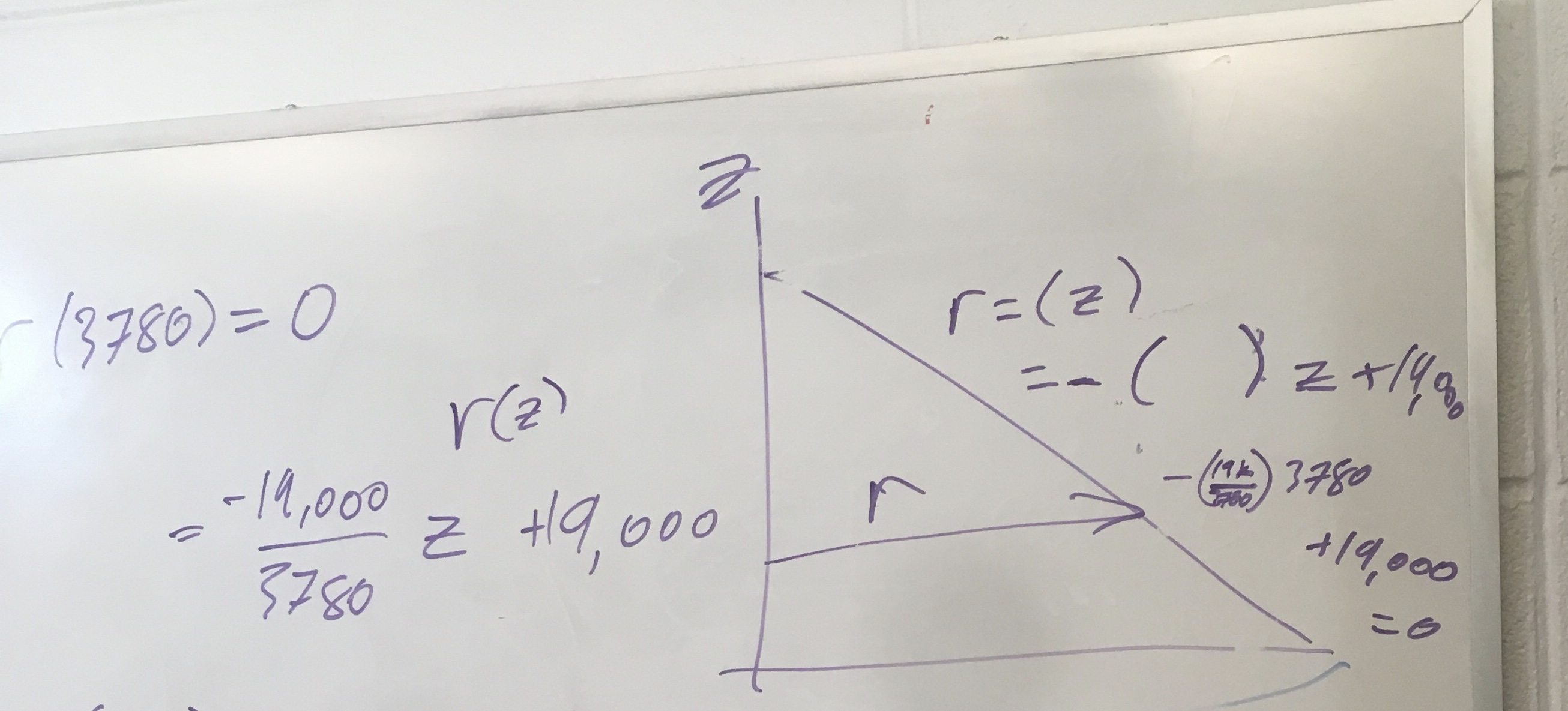
Thinking of Mt Fuji as a right-circular cone, with a radius at the base (at $z$=0 m) of 19,000 m, and a radius at the top ($z$=3780 m) of 0 m, we can write an expression for $r(z)$: $$r(z)=19000 -\left(\frac{19000}{3780}\right)z = 19000 -5.03z.$$ So, we could calculate the volume of Mt Fuji from a triple integral, in Cylindrical coordinates, where $\theta$ runs from 0 to $2\pi$, $z$ runs from 0 to 3780, and $r$ runs from 0 to the $r(z)$ (the function above). Translating this into the limits on a triple integral... $$\begineq V &= \iiint\,dV=\iiint rdr\,d\theta\,dz\\ &= \int_{z=0}^{3780}\int_{\theta=0}^{2\pi}\int_{r=0}^{19000-5.03z}rdr\,d\theta\,dz \endeq$$
The limits on the triple integral will be the same as what we used to calculate the volume, So the total energy is... $$\begineq &E=\iiint dE=\iiint gh\,dm =\iiint g z \rho\, dV\\ &=\int_{z=0}^{3780}\int_{\theta=0}^{2\pi}\int_{r=0}^{19000-5.03z}10*z*3200*rdr\,d\theta\,dz\\ &=\int_{z=0}^{3780}\int_{\theta=0}^{2\pi}\int_{r=0}^{19000-5.03z}32,000zr\,dr\,d\theta\,dz\\ \endeq$$ CoCalc says this is $E=4.32\times 10^{19}$ Joules
- Carry out the integral by hand, take a picture of your work, and hand in the picture on Moodle,
- Or, carry out the integral in a CoCalc notebook. Export your notebook to .pdf, and hand in the .pdf on Moodle.
Your answer above is in Joules (J).
A large coal power plant, or nuclear plant, has power output of 2 gigawatts=2,000 megawatts=$2\times10^{9}$Joules/second: In a year of continuous operation it puts out
$6.3\times 10^{16}$J.
How many months or years would such a power plant need to operate to produce the energy content you calculated above?
This would take $4.32\times 10^{19}$ Joules / $6.3\times 10^{16}$ Joules per year \approx$ 685 years!