Green's theorem problems

1. Let $C$ be the triangle path $(0,0)\to(1,1)\to(0,1)\to(0,0)$.
   

   show / hide solution

   The orientation of the path is negative. So, multiplying by $-1$, The vector integral around the outside is equal to the positive orientation: $$\begineq \oint_{-C}(-2y\,dx+3x\,dy)&=&\\ \oint P\,dx+Q\,dy &=&\iint\left(\frac{\del Q}{\del x}-\frac{\del P}{\del y}\right)\,dA\\ &=&\iint\left(3-(-2)\right)=5\iint dA=5*\frac 12. \endeq$$ =5/2.

2. Use Green's Theorem to calculate $\oint_C(y-x)\,dx +(2x-y)\,dy$ where $C$ is the boundary of the rectangle shown.
   
   

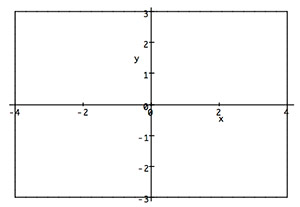
   show / hide solution

   $$Q_x-P_y=2-1=1$$ so $$\oint_C P\,dx+Q\,dy=\int_{-4}^{4}\int_{-3}^3 (1) \,dx\,dy=8\times 6.$$ =48

3. Compute $\oint_C\left(-\frac{xy^4}{2}\right)\,dx + \left(x^2y^3\right)\,dy$ where $C$ is the curve shown below.
   
   

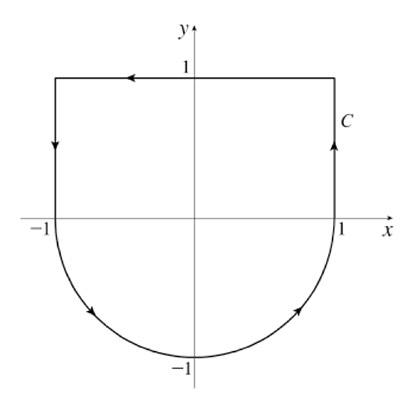
   show / hide solution

   $$Q_x-P_y=2xy^3-(-4xy^3/2)=4xy^3$$ then $$\begineq\oint_C...&=&\int_{x=-1}^1\int_{y=-\sqrt{1-x^2}}^1 4xy^3\,dy\,dx\\ &=&\int_{x=-1}^1 4x \left(\int_{y=-\sqrt{1-x^2}}^1 y^3\,dy\right)\,dx\\ &=&\int_{x=-1}^1 4x \left( \left.\frac{y^4}{4}\right|_{-\sqrt{1-x^2}}^1 \,dy\right)\,dx\\ &=&\int_{x=-1}^1 \frac{4x}{4} \left(1-(1-x^2)^2 \right)\,dx\\ &=&\int_{x=-1}^1 x (2x^2-x^4)\,dx=\int_{x=-1}^1 (2x^3-x^5) \,dx\\ &=&\left[\frac{2x^4}{4}-\frac{x^6}{6}\right]_{x=-1}^1=\left[\frac24-\frac24-\left(\frac16-\frac16\right)\right] \endeq$$ =0

4. Use Green's Theorem to evaluate the following line integrals:
   1. $\oint_C\left(\arctan(x^2)-y^2\right)\,dx+ \left(x^2y-\ln(y^2+1)\right)\,dy$ where $C$ is the semicircle $y=\sqrt{4-x^2}$ together with the line segment $(-2,0)\to(2,0)$ as shown.
      
      

      show / hide solution

      $$Q_x-P_y=2xy-(-2y)=2y(x+1).$$ So, $$\begineq \oint_C...&=&\int_{x=-2}^2\int^{\sqrt{4-x^2}}_{y=0} 2y(x+1)\,dy\,dx\\ &=&\int_{x=-2}^2 2(x+1)\int_0^{\sqrt{4-x^2}} y\,dy\,dx\\ &=&\int_{x=-2}^2 2(x+1)\left.\frac{y^2}{2}\right|_0^{\sqrt{4-x^2}}\,dx\\ &=&\int_{x=-2}^2 2(x+1)\frac12 (4-x^2)\,dx\\ &=&\int_{x=-2}^2 (x+1)(4-x^2)\,dx=\int_{x=-2}^2 4x-x^3+4-x^2\,dx\\ &=& \left.\left(\frac{4x^2}2-\frac{x^4}{4}+4x-\frac{x^3}{2}\right)\right|_{x=-2}^2\\ &=& 0 - 0 + 16-8 \\ \endeq$$ =8
      

   2. $\oint_C xy\,dx+(x^2+y^2)\,dy$ where $C$ is this triangle.
      
      
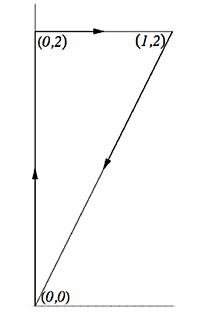
5. Consider the non-closed curve $C$, $(3,0)\to(0,2)\to (1,0)$ as shown. Figure out a way to use Green's Theorem to help you compute $\int_C(x+y)\,dx+(3x-y)\,dy$.
   
   Hint:
   

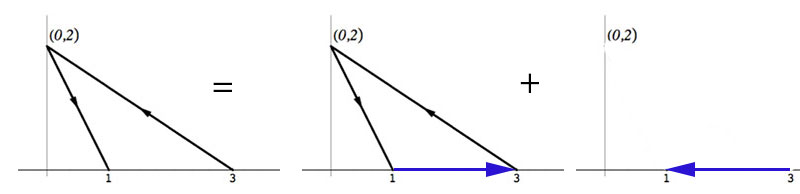
   show / hide solution

   $\myv F=P\uv i+Q\uv j$ With $P=x+y$ and $Q=3x-y$,
   
   The vector integral $\oint_\text{triangle}\myv F\cdot\,d\myv r$ all the way around the triangle above is, according to Green, given by the double integral: $$\nonumber\iint Q_x-P_y\,dA=\iint (3-1)\,dA=2*A=2*(\text{base}*\text{height}/2)=4.$$
   The vector line integral along the path above ($d\myv r=dx$ and $y=0$) is $$\nonumber\int \myv F\cdot\,d\myv r=\int_3^1P(x,y=0)\,dx=\int_3^1x\,dx=\left.\frac{x^2}2\right|_3^1=\frac 12 -\frac92=-4$$

   Adding the two contributions together: 4-4=0.