[9.1] - Review / Preview
We started in on section 9.1 in Schlicker's "Active Calculus". With what we discussed about the distance formula, you should be able to answer questions 1 and 2 below.
Now Read section 9.1.4 and 9.1.5 on Traces and Contour Maps/Level curves. Then complete question 3.
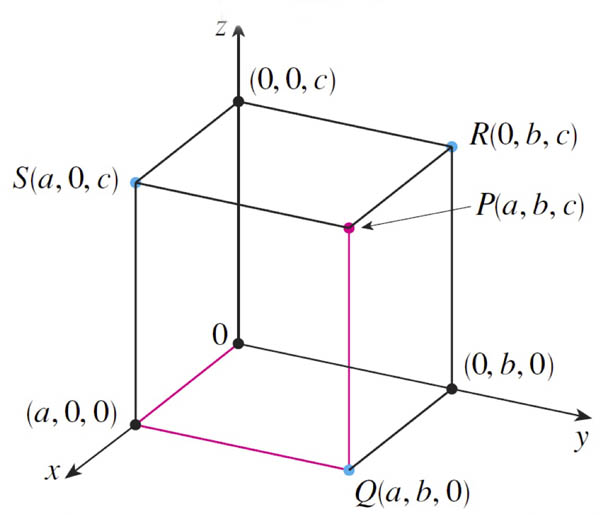Consider the point $P=(x,y,z)$ [I'm using an older diagram here. Just translate these
parameters in the diagram to this notation: $a\to x; b\to y; c\to z$.]
- What are the coordinates of the closest point to $P$ on the $x$-axis? And what is the distance between these two points?
Closest point, $Q$, has the same $x$ coordinate. But to be on the $x$ axis $y=0$ and $z=0$, so $Q=(x,0,0)$
Distance $PQ$ is $\sqrt{(x-x)^2 + (y-0)^2 +(z-0)^2}=$ $\sqrt{y^2+z^2}$ . - What are the coordinates of the closest point to $P$ on the $yz$ plane? And what is the distance between these two points?
The $yz$ plane means $x=0$. Closest point is $R=(0,y,z)$ .
The distance $PR$ is $\sqrt{(x-0)^2+(y-y)^2+(z-z)^2}=$ $|x|$ (absolute value of $x$).
- What are the coordinates of the closest point to $P$ on the $x$-axis? And what is the distance between these two points?
- The work above should help you answer
Schlicker's question 8 [in section 9.1]. Record your answers to question 8 below.
With what we did above, we can answer part b) first: The points whose distance from the $x$-axis equals the distance from the $yz$ plane means... $$\begineq \sqrt{y^2+z^2} = |x|\\ y^2+z^2 = x^2\endeq$$ This is the last equation in b.)
a.) The term on the left represents a circle in the $yz$ plane centered on $(y,z)=(0,0)$ (which is where the $x$ axis is...) and the term on the right means that the radius is $x$. So as the $x$ coordinate grows, the radius of the circle grows too. So this is A cone opening along the $x$-axis.
- Answer Schlicker's question 13 and record your answers below. [Hint: You can use Geogebra to graph an equation and a plane together.]