9.6 - The matching game
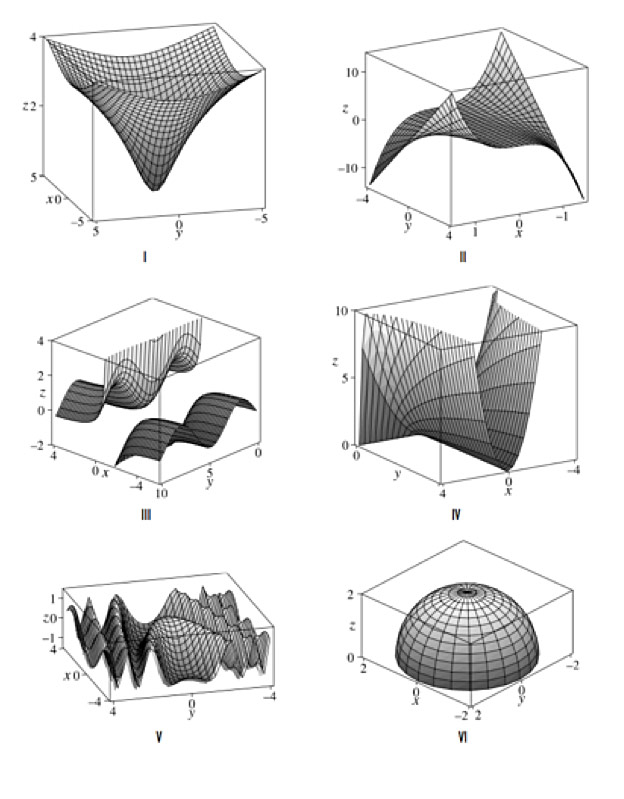
Match each function with its graph. Give reasons for your choices. (Your reasons might include arguments involving traces of $x$, $y$ or $z$)
| 1) $f(x,y)=\frac{1}{x+1}+\sin y$.
the fraction blows up as $x\to-1$. Otherwise, if $x=k$, then $z\propto C+\sin(y)$.
|
2) $f(x,y)=\sqrt{4-x^2-y^2}$
Horizontal traces ($z=k$) are circles. Impossible for $z$ to be greater than $\sqrt 4=2$. |
| 3) $f(x,y)= \cos(x+y^2)$
If $y^2=k$, then $z\propto \cos(x+k)$. Also, the $\cos(\text{ })$ function never gets above 1 or below -1, so $-1< z < +1$ as well. |
4) $f(x,y)=\ln(x^2+y^2+1)$
Lowest possible value occurs when $x=y=0$: $f(0,0)=\ln 1=0$.
Horizontal traces are circles. |
| 5) $f(x,y)=x^2\sqrt y$
If $y=k$, $z\propto x^2$. If $x=k$, $z\propto \sqrt y$. Undefined for $y\lt 0$. |
6) $f(x,y)=x^3y$
When $y=k$, $z\propto x^3$. When $x=k$, $z\propto x$. |