[11.2] - Area between curves
This desmos graph has a better representation of the function $x=y^{\frac 14}$ than the plots below for b and c. Use the desmos one to estimate areas.
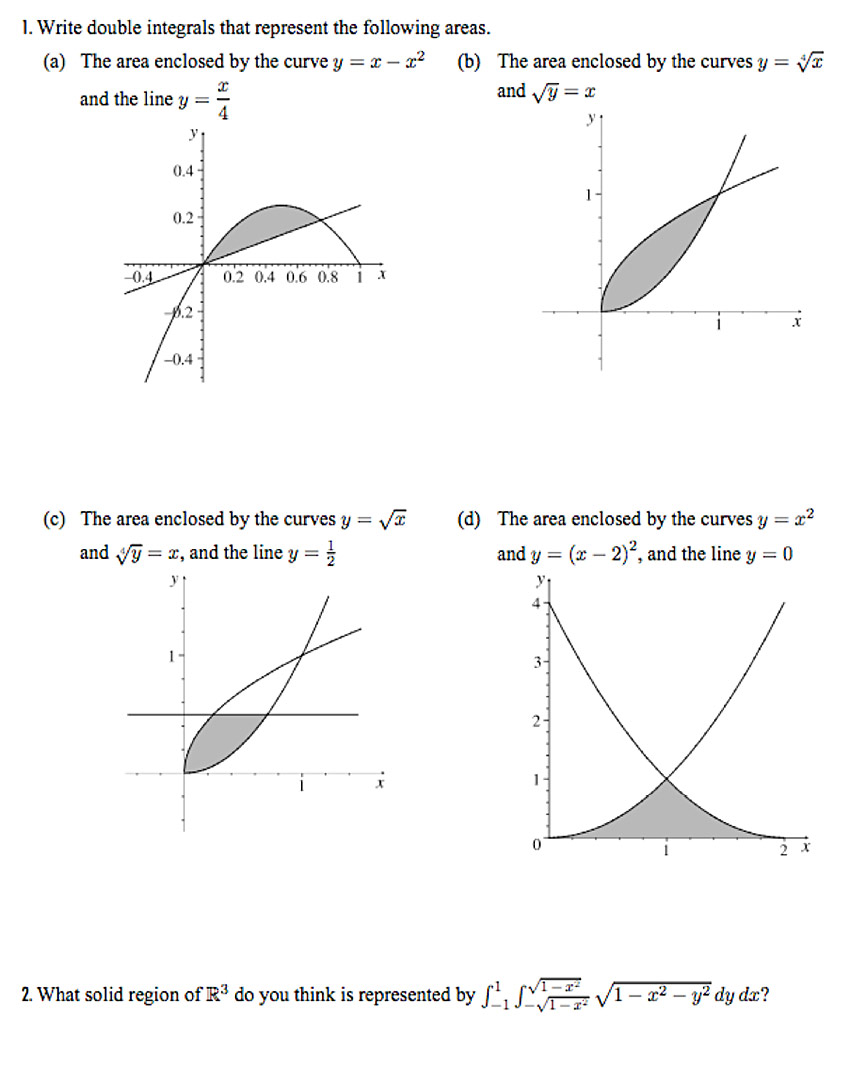
a. $$\int_{x=0}^{3/4}\int_{y=x/4}^{x-x^2}dy\,dx$$ =0.070
b. Solving for $y$ by squaring both sides of $\sqrt{y}=x$ gives us $y=x^2$. $$\int_{x=0}^{1}\int_{y=x^2}^{\sqrt[4]{x}} dy\,dx$$ =7/15
c. Now we want functions $x(y)$ of $y$. Solving $y=\sqrt x$ for $x$ gives $x=y^2$ which is the function closest to the $y$ axis. $$\int_{y=0}^{1/2}\int_{x=y^2}^{\sqrt[4]{y}} dx\,dy$$
d. When solving for $x$, we take the square root of both sides of $y=(x-2)^2$. The left side could be either $-\sqrt y$ or $+\sqrt y$. The shape works out right if you choose the negative root, and then
$$
\int_{y=0}^1\int_{x=\sqrt y}^{2-\sqrt y} dy\,dx.$$
=2/3
2.) Think of $\sqrt{1-x^2-y^2}$ as the surface $z=\sqrt{1-x^2-y^2}$. Then think of the argument of the integral as the difference between two functions, $z(x)-0$....
And the integral can be written: $$\int_{x=-1}^{1}\int_{y=-\sqrt{1-x^2}}^{+\sqrt{1-x^2}} \int_{z=0}^{\sqrt{1-x^2-y^2}}dz\,dy\,dx=\frac23 \pi$$ ...because we are integrating $dV=dz\,dy\,dx$ over a region which is half of a sphere of radius 1!