Half-lives & Dating

Throwing dice

 

Throw 600 dice into the air all at the same time.

How many are likely to come down showing a 3?

a.) 1   b.) 5   c.) 10   d.) 50   e.) 100   f.) 500  

show / hide

There are 6 sides to a regular dice. So the probability that a rolled dice will come as a '3' is 1/6.

So, we'd expect that, for a large collection of dice, approximately 1/6 of the dice would be showing '3'. (And 1/6 would show '1', and 1/6 would show '2'....).

So, out of 600 dice, we'd expect $600*\frac 16=100$ dice would show a '3'

Remove all the 3s, and on average you would expect to have 500 dice left over.

Now, continue this process: Imagine that you toss the dice up, and each time you remove all the dice that come up '3'. On average, you would expect to lose 1/6 of the number of dice with each throw.

And so, we can assemble a table of how many dice are left after each toss:

number of throws	$N_\text{dice}$	$N_\text{dice}$
$0$	$600.0$	$600.0*\left(\frac 56\right)^0=600.0$
$1$	$600.0-\frac 16 600.0=500.0$	$600.0*\left(\frac 56\right)^1=500.0$
$2$	$500.0-\frac 16 500.0=416.7$	$600.0*\left(\frac 56\right)^2=416.7$
$3$	$416.7-\frac 16 416.7=347.2$	$600.0*\left(\frac 56\right)^3=347.2$
$4$	$347.2-\frac 16 347.2=289.4$
$5$	$289.4-\frac 16 289.4=241.1$
$6$	$241.1-\frac 16 241.1=201.0$
$7$	$201.0-\frac 16 201.0=$___	$600*\left(\frac56\right)^7=$___

As was the case with exponential growth, several different ways are shown for how to calculate the number of dice left over after "$x$" tosses.

The way of calculating the dice looks like it has a lot in common with exponential growth. But in this case, the number of dice is decreasing by a certain fraction with each toss, instead of increasing by a fraction. So we call this process...

Exponential decay

We saw that for an exponential growth process, such as money on deposit, the money in a savings account increased by the same fraction (or same percentage) each year. One equation that gave the total amount of money on account was: $$y(x)=P\cdot(1+r)^x.$$

• $P$ is the amount you started with (at $x=0$).
• $r$ was the fraction by which your money increased each year. Or, if you know the percentage growth rate, you can divide that percentage by 100 to get the fractional rate of growth.
• $x$ was the number of years.

But in the case of throwing dice and taking out the 3's, the number of dice is decreasing by the same fraction with each toss. Instead of a growth process, we call this an exponential DECAY process.

The number of tosses is like the time in exponential growth processes. And we also have a fraction of decrease. So, perhaps you will not be too surprised that the formula for the number of dice left over after $x$ tosses, if we take out a fraction, $r$, each time, is:

Exponential decay process: $$y(x)=P\cdot(1-r)^x.$$ There is a minus in front of $r$ instead of a plus. This means that (1-r) is less than one. And mulitiplying any number by a number less than 1 gives a smaller number.

Now, perhaps you can see why there is a fraction $\frac 56$ in the last column of the table:

• The fraction of dice we're losing with each toss is $r=\frac 16$.
• We're starting with $P=600$ dice.
• If $x$ is the number of tosses,
• Then the formula for the number of dice left after $x$ tosses will be $$y(x)=600\cdot\left(1-\frac 16\right)^x=600\cdot\left(\frac 66-\frac 16\right)^x=600\cdot\left(\frac56\right)^x.$$

Half-life

An exponential growth process is characterized by a constant doubling time, $d$.

But an exponential decay process is characterized by a constant half-life, $h$.

In the case of our dice, it should take $h$ tosses for the number of dice to drop from 600 to 300. And then it should take another $h$ tosses for the number of dice to drop from 300 to 160.

There is another formula to calculate the number of dice left after a time, $x$, in terms of the half-life, $h$: $$y(x)=P\cdot\left(\right)^{\frac xh}.$$ You can look at what is similar and different from the formula for exponential growth in terms of a doubling time.

Isotopes and adioactive decay

Here are some observations about atoms:

• The nucleus consists of protons and neutrons,
• A proton and a neutron have almost the same mass.
• An electron is much lighter. The mass of an electron is about 1/1800 of that of a proton.
• So most of the weight of an atom is in the nucleus
• The electrical charge of a proton is the same, but opposite, of the charge of an electron.
• So, in an electrically neutral atom, there will always be the same number of electrons and protons. This number is called the atomic number. For example, the atomic number of hydrogen is 1, the atomic number of carbon is 6.
• The chemical interactions of an atom depend only on the atomic number.
• Some Carbon

The chemical properties of an atom are determined by it's electrons. And there are just as many electrons as protons in an electrically isotopes are unstable. We call these unstable ones radioactive isotopes. After a time, the nucleus of an unstable atom gives off some sort of particle, and decays (or turns into) a different nucleus, called the daughter nucleus or daughter isotope.

If we have some "chunk" of radioactive matter, we can monitor the process of decay by counting the particles given off with a radiation detector. Here is some data we have gotten in past classes, by monitoring a sample of barium-137, $Ba^{137}$: 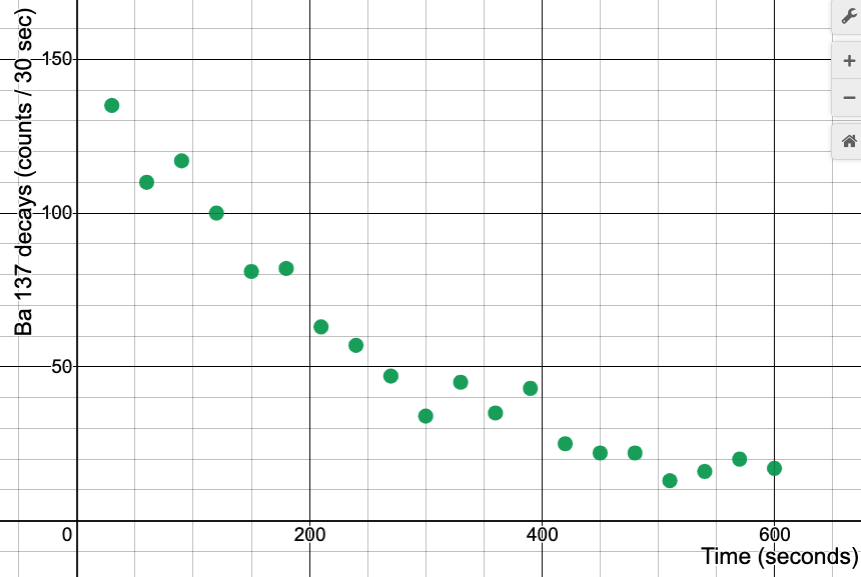XXX

---

Exponential decay

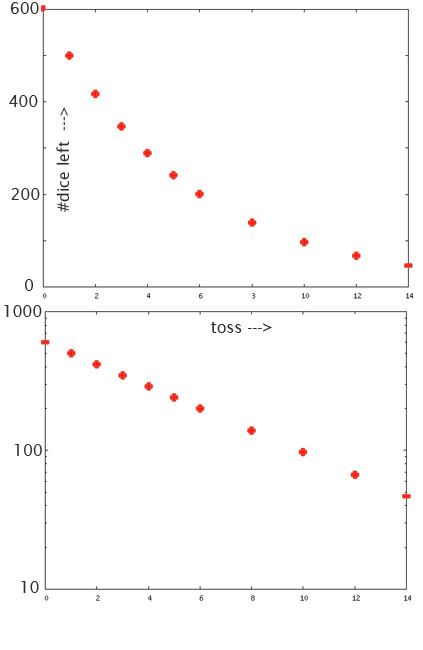
Exponential growth: a "J"-curve, straight on a semi-log plot, characterized by doubling time.

Dice-ish data:a "reversed J"-curve, straight on a semi-log plot, characterized by a half life.

Each dice has a characteristic probability that a "3" will be rolled in one toss: 1/6.

Each radioactive nucleus has a characteristic probability that it will decay in a second.

If the dice are tossed once per minute, what is the half-life for the number of dice: The time after which we have only half of the original number of dice?

Say you have 100 coins, and you throw them all up in the air once each minute, and then remove all the heads. What is the "half-life" for the number of coins left in minutes?

What if people died like radioactivity works?

It is worth pausing to consider how weird this is:

The current world average lifespan at birth is 67.2 years.

If we died with a half-life of 67.2 years:

• Half the population born in 1990 would die by 67--in 2057, but half of the population would still be alive.
• 67 years later, (age 134) half of the survivors would be dead, but half (1/4 of the initial population) would still by alive.
• 67 years later, (age 201 in the year 2191) 1/8 of those born in 1990 would still be alive.

Humans seem to have a pretty firm "expires by" date, but not radioactive atoms.

Half-lives

Carbon dating

Where do radioactive isotopes come from? We will find that many elements were made in stars.

There are 2 processes that affect ${}_6^{14}C$ in Earth's atmosphere. (Carbon in the atmosphere is mostly present in the chemical compound $CO_2$):

• ${}_6^{14}C \rightarrow {}_7^{14}N + {}_{-1}^0 \beta$
  Radioactive decay with a half-life ~6000 yrs.
• ${}_7^{14}N + {}_{-1}^0\beta \rightarrow {}_6^{14}C $
  Extra-terrestrial particles bombard Earth, including energetic betas ($\beta$'s, or electrons).

Eventually a balance is reached where the number that decay each year is ~ equal to the number of new ${}_6^{14}C$ nuclei produced each year.

This equilibrium ratio is about

1 ${}_6^{14}C$   :   1 trillion ($10^{12}$) ${}_6^{12}C$

Photosynthesis

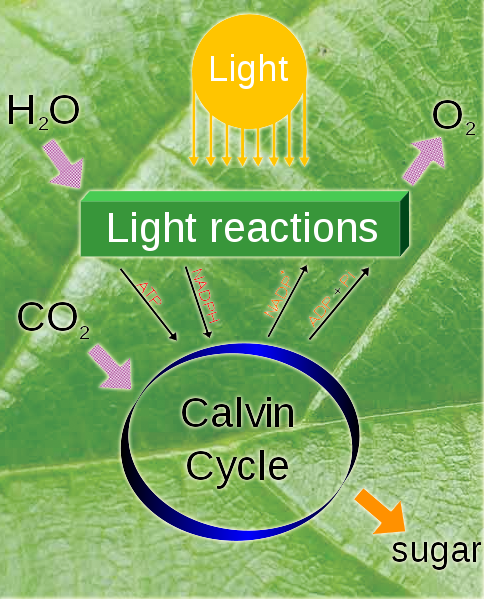
Plants inhale ${}_6^{14}C$-containing $CO_2$ while alive, and use this carbon to store sugars, build cell walls, etc.

While alive, their ${}_6^{14}C$:${}_6^{12}C$ ratio is... the same as the atmosphere: ~ 1:trillion.

Plant death

Death means no new $CO_2$ coming in.
Carbon-14 decays to nitrogen, but no new ${}_6^{14}C$ is arriving. Grind up old leaves, and count the isotopes (in a mass spectrometer)...

${}_6^{14}C$ : ${}_6^{12}C$ ratio	Age (years)
1.0 : 1 trillion 0.5 : 1 trillion 0.25 : 1 trillion 0.13 : 1 trillion	0 6,000 12,000 18,000

1. How many years after a plant dies until its Carbon-14 : Carbon-12 ratio drops below 1% of what it was when it was alive? [instead of 1 : 1 trillion it is below 0.01 : 1 trillion.]
2. Once an atom of Carbon-14 is produced in the upper atmosphere, what is the probability that it will decay sometime in the following 6000 years?
   1. More than 50%,
   2. 50%,
   3. Less than 50%?
3. A particular atom of Carbon-14 was generated in the atmosphere 100,000 years ago, and it hasn't decayed yet to Carbon-12. In the next 6000 years, what is the probability that this atom will decay?
   1. More than 50%,
   2. 50%,
   3. Less than 50%?

   How would we know if this really works?

   
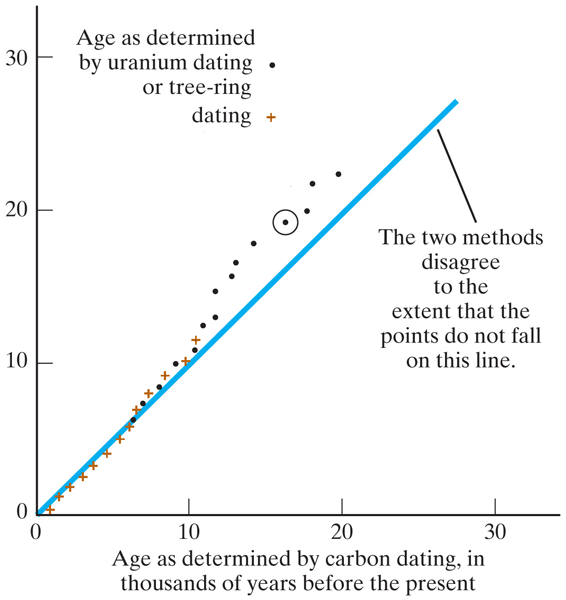
   Check against against tree-rings: take carbon samples from different rings. Compare the ring count with the date you get from the Carbon-14 : Carbon-12 ratio.

   Alcohol *has to be* radioactive

   The U.S. Department of Alcohol, Tobacco, and Firearms tests alcoholic beverages and will not allow it to be sold unless it has "enough" radioactivity. Why?

   There is a law in this country that alcoholic beverages may only be made from fresh fruits, and in particular not from petroleum products.

   Petroleum is the remains of plant matter, but it has been underground for 10's or 100's of millions of years: Many, many half-lives of Carbon-14 (half-life=6000 years).

   $\Rightarrow$ Petroleum will have virtually no Carbon-14, and therefore no Carbon-14 decays. So looking for radiation from Carbon-14 decays is an easy way to test for petroleum vs recent fruits.

   Ancient temps from ${}^{18}O$ : ${}^{16}O$

   All three naturally occuring oxygen isotopes are stable: ${}^{16}O$ (99.762% natural abundance), ${}^{17}O$,${}^{18}O$. So, assume no change in terrestrial isotope ratios.

   Heavy water: $H_2O$ molecules with the heavier oxygen isotopes are heavier.

   Evaporation

   High temps: at extremely high temps (boiling) all water molecules go liquid $\rightarrow$ vapor.

   Low temperatures: It's more likely for thermal jostling to kick a lighter $H_2O$ from liquid $\rightarrow$ vapor than a heavier one $\Rightarrow$

   • Atmosphere is enriched in oxygen-16 $\Rightarrow$oxygen-16-rich water vapor falls as snow in Greenland and forms one ice layer per year.
   • Oceans are enriched in oxygen-18 $\Rightarrow$ benthic (marine life) skeletons / shells are rich in oxygen-18.

   IPCC data for climate from years ago

   

   Brief history of Earth

   

   Suggested exercises

   Chapter 14, Conceptual Exercises: 17, 19, 21, 34, 35

   Image credits

   Oliver Kurmis, Ian Turk, Kurzon, Yzmo, Daniel Mayer, Peter Pick, water vapor, Torsten Reuschling