Sun / latitude observations

Here we are, in our little home in the universe!

After introducing the idea of solar noon, we'll explore how the sun's elevation angle at solar noon changes throughout the year, and how this differs from the North Star.

Download the .pdf of this activity to be able to write on it.

Back to Polaris...

Yes, there's Polaris. Its azimuthal angle is zero (="North"), and its elevation angle in Goshen is about 42${}^o$ above the North horizon--Goshen's latitude.

One of the really striking things about the North star is that its elevation angle is always the same!

  • at 1 am, at 2 am, at 3 am...
  • in January, in February, in March...

Not so for the sun!

  • Sunrise occurs when the sun peeks over the horizon (elevation angle = 0${}^o$), somewhere in the East (Straight E= azimuth angle of 90${}^o$ clockwise from N)
  • The sun rises (increasing elevation angle) in the sky...
  • ...until solar noon="high noon", when it's at its highest elevation in the sky. At this point its azimuthal angle should be half-way between East and West.

    What *two* directions are "half-way between" East and West? What are the azimuthal angles of these two directions?



  • Then, it drops down towards the horizon (decreasing elevation angle)...
  • Eventually it sets somewhere in the West (Straight W= azimuth angle of -90${}^o$, or more conveniently, 360-90 = 270${}^o$.

To make matters more complicated, the elevation angle of the sun at solar noon is not the same from day to day. It changes throughout the year, and this is related to the changing length of the day as well.

"Straight" Earth

Before we go any further, Consider again our picture of the Earth with latitude markings (below):

You might also consult these interactive graphs:

  • Polar / Latitude lets you vary the latitude and picture the elevation of Polaris above the horizon.
  • Sun / Latitude lets you vary the latitude and picture the elevation of the sun above the horizon (at "high noon").

Now...

  1. Make a mark / draw a little human at about 42${}^o$ N latitude on the right side of the Earth circle.
  2. The rays from Polaris are all coming straight *down* towards Earth, parellel to the axis of rotation. (Draw some Polaris rays).
  3. Imagine that the sun was straight above the equator, to the right in this picture. Draw some rays from the sun, which are all parallel.
  4. So, a person at the equator would see the sun straight up above: "High noon".
  5. Anyone on the right side of the circle would be experiencing the sun at its highest point in the sky (also solar noon).

Now use a little geometrical thinking to puzzle out what the elevation angle of the sun would be: You can probably see that there's a right angle between Polaris' rays and the Sun's rays. And, while Polaris' angle is above the North horizon, I think you can see that the sun's elevation angle would be above the South Horizon.

The sun's elevation in Goshen (Latitude=42 degrees) at high noon above the South horizon would be:




The sun's changing elevation angle

We'll explore how the sun's solar noon elevation angle changes by looking up the sun's elevation at solar noon using the National Oceanic and Atmospheric Administration's (NOAA) solar calculator website. To use that:

  1. Follow the instructions to zoom in, pick up one of the pins already on the map, and then drop it on Goshen. (or enter the latitude and longitude of Goshen...)
  2. Choose as the date, 21 Jan 2020
  3. In the Result section you'll see the time of solar noon.
  4. Copy that time into the Local Time box above.

Now the Az/El, Azimuth and Elevation, at Local Time is displayed in the results.

Make a graph in Desmos of the elevation angle at solar noon versus the month (21st of each month)

  1. If you haven't already made an account on Desmos.com, make one. This will allow you to save and share graphs you make:
  2. Click the + and choose table. In this table, $x_1$ will be the number of the month (1=Jan, 2=Feb, etc...) and $y_1$ will be the elevation angle of the sun at solar noon (in Goshen).

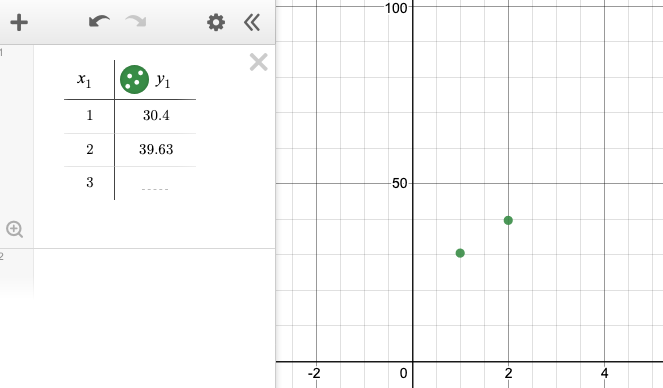
  3. Switch back and forth between the NOAA solar calculator and Desmos, and enter your elevation angle for the sun at high noon for the 21st day of each of the 12 months.

Fitting the data

Desmos allows you to fit a function that has some parameters (numbers) in it to data. Your data probably looks roughly like a sine (or cosine) function with a period of 12 months (the 12 below). The general equation for such a function is: $$a+A\sin\left( \frac{2*\pi}{12}*(x-s) \right).$$ In this equation, $a$ is the average value of the function, and the function varies from a low value of $a-A$ to a high value of $a+A$. We say that $A$ is the amplitude of oscillation.

You'll fit your data like this:

  1. Hit + and insert a new "expression".
  2. Type out your formula like this,

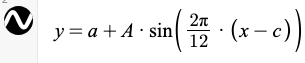
    typing pi to get the pi symbol.
  3. When you're asked if you want all the sliders, say yes.
  4. After you've typed it out, go and change all the sliders to run from 0 to 50

Now play around with the sliders and see what each one does.

To get the computer to do the fitting:

  1. Modify your formula to look like this:

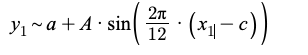
    Make sure your subscripts match the ones in your table, and use ~ instead of "=".

When you've got the fitting to work, save your Desmos graph, and paste the URL of that graph in here:


Your average value parameter $a$: What was it, and how does it compare with your guess about the "straight Earth"?



If Earth was always straight to the sun (that is, the sun was always straight above the Equator, throughout the whole year) what would $A$ have to be, so that the elevation of the sun would not be changing?



But instead you have a varying maximum angle. What is your value of $A$ and what do you think that means about Earth's position relative to the sun? (You may include a sketch if that's helpful.)