"Air" resistance
- Series expansion of friction forces in 2 powers of speed
- Linear friction (viscosity)
- Quadratic friction (energy of swirliness)
- Flow and Reynolds number
- Low speed : laminar flow
- High speed : turbulent flow
- Vehicles (and rolling resistance)
See also
- Drag (Wikipedia)
- Reynolds Number (Wikipedia)
Air resistance
An object moving through a fluid medium--by which I mean a liquid or a gas--encounters resistance (that is, a force) which is exactly opposite its motion.
This force does not exist without motion of the object relative to the medium, so it seems reasonable to make the force a function of the speed v (possibly a complicated function). $\myv{f}$ $ = -f(v) \uv{v}$
That is to say, we'll be considering problems like the one on the left, where we'll neglect an additional lift force (which is not always negligible).
Linear and Quadratic components
As long as we're well below the speed of sound of the medium ( ~ 770 mph for air at STP) the force on a moving object can be approximated with the first two terms of a power series... $$f(v)= bv +cv^2=f_1+f_2$$
- The linear term is associated with viscous drag (sliding friction). It dominates at low speeds.
- An object with area $A$ moving at a constant speed, $v$, sweeps out a volume $Avt$ in time $t$. The quadratic term arises from the work it takes to accelerate the "fluid" in this volume up to the same speed $v$ as the object. [Problem 2.4]. This term dominates at higher speeds.
For water flowing in a pipe, we have laminar flow for slow speeds. As the speed of the water increases, the flow becomes turbulent.
Viscous drag
The
linear drag term is proportional to $\beta$ which is characteristic of the medium and a
typical linear dimension $D$ of the object.
$$f_1 = bv = \beta D v$$
In laminar flow, think of the molecules of the medium as being part of "curtains" parallel to the flow. As the object passes, the curtains move away from the object, and then back to their original places but with no net change in kinetic energy.
Friction arises from the drag with the "curtains". So the dimension $D$ is a typical linear dimension of an object parallel to the direction of the flow. ($\beta$ is proportional to the viscosity, but see Taylor's equation 2.82 for viscosity...)
For a sphere in air at standard temperature and pressure (STP), $D$ is the diameter of the sphere and $\beta = 1.6 \times 10^{-4}$ N sec / m$^2$.
Pure linear resistance is associated with laminar flow, and is the only source of resistance at low Reynolds numbers (Re < 1).
Quadratic drag
The quadratic drag term arises when the flow is turbulent: The object is moving fast enough to be having head-on collisions with molecules in the medium.
During a time $t$ at constant speed $v$, an object of cross-sectional area $A$ moves a distance $d=vt$. It must accelerate (impart additional kinetic energy to) the molecules in a tube of volume $Ad=Avt$. The molecules are accelerated up to $\approx$ the speed of the object.
- See "Sustainable Energy Without the Hot Air". David MacKay has an analysis of energy use by cars along these lines.
- $Re = D\rho v/ \mu $
- $D$ is a 'typical' length of the object parallel to the flow,
- Air: $\rho= 1.3$ kg /m${}^3$ ; $\mu = 1.8 \times 10^{-5}$kg/(m s).
- Read 2.2 and 2.3
- Problem 2.4
Therefore, the frictional force is proportional to the density of the medium and the cross-sectional area $A=D^2$, where $D$ is a 'typical' object dimension perpendicular to the direction of flow of the medium around the object. $$f_2 = cv^2 = \gamma D^2 v^2$$
For a sphere in air at (STP), $D$ is the diameter of the sphere and $\gamma = 0.25$ N sec$^2$ / m$^4$.
Reynolds Number
Can we neglect $f_1$ or $f_2$ for a particular problem? That depends on the dimensionless ratio: $$\frac{f_2}{f_1} = \frac{cv^2}{bv}\frac{\gamma D^2v^2}{\beta D v}=\frac{\gamma D}{\beta}v.$$ where the final result is according to our approximations for a sphere.
Using our values for $\beta$ for air, and $\gamma$ for a sphere in air, this gives $f_2/f_1= 1.6 \times 10^3 \frac{\text{s}}{\text{m}^2}Dv$.
The Reynolds Number, $Re$, is also a dimensionless number used by engineers to characterize flow, and proportional to $Dv$: $$Re = \frac{D\rho v}{\mu} .$$ Where $\rho$ is the density of the material, and $\mu$ is the viscosity. At STP $\rho=1.225$ kg/m^3 and $\mu=1.8\times 10^{-5}$ kg / (m s) (the "dynamic" viscosity).
For air at STP we get $\rho/\mu=69\times 10^3 \frac{\text{s}}{\text{m}^2}$. So in this case the Reynolds number for sphere is $Re\approx 45 \frac{f_2}{f_1} $ for a sphere in air: The Reynolds number for identical spheres at identical speeds would be about 45 times greater than the ratio of their quadratic/linear forces by a factor of 45, or approximately 1.5 orders of magnitude greater than our sphere-specific result calculated above.
Osborne Reynolds, "An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels", Philosophical Transactions of the Royal Society (1883).
Problem 2.3
In the case of a sphere in air, with density and viscosity $\rho= 1.275$ kg /m${}^3$ ; $\mu = 1.78 \times 10^{-5}$kg/(m s), we get $Re = 72 \times 10^3 $s/m${}^2 Dv \approx 48 \frac{f_2}{f_1}$ (problem 2.3).
Flow in a pipe
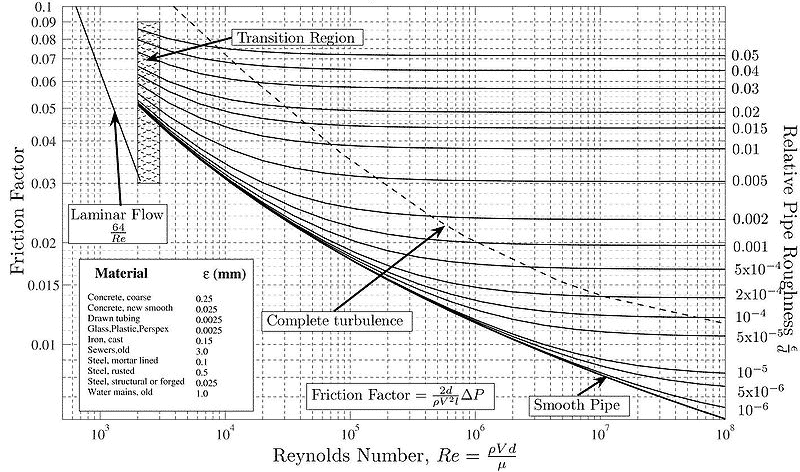
A Moody Diagram relates pressure drop in a non-ideal pipe via a non-dimensional friction factor to the Reynolds number of the flow. A clear transition from laminar to laminar + turbulent flow is seen between $10^3 < Re < 10^4$.
Cyclist
Estimate the
Reynolds number for a cyclist moving at a 'typical' speed, using:
Let's say $D\approx 1$ meter and $v=12$ mph=5.4 m/s. Then
$$Re = D\rho v/ \mu=(1)*(1.3)*(5.4)/(1.8 \times 10^{-5}=390,000.$$
And from our considerations above, the ratio of quadratic resistance / laminar force should be $f_2/f_1=Re/45 \approx 8700$ so quadratic air resistance is by far the dominant force.
We'd have to be going well below 1 mph for linear resistance to dominate quadratic.
Vehicles on the surface of Earth
For vehicles, there are a bunch of miscellaneous sources of drag related to frictional losses in wheel bearings, shaking and vibration of the vehicle (and the road bed) flexing of the wheels/tire casings. These forces are collectively called "rolling resistance". They are approximately independent of speed, and vary with the weight of the vehicle. So we could write: $$f(v)=f(v)= bv +cv^2 + dmg.$$
But since the viscosity of air is pretty low, and the viscous force drops as $v$ already, the dominant force of resistance for vehicles at low speeds is not viscosity but rather rolling resistance. So practically, a good approximation is: $$f(v)\approx cv^2+dmg.$$
MacKay points out that the two principle ways that cars use energy include 1.) Fighting quadratic air resistance, and 2.) Accelerating the mass of the car from 0 to cruising speed between stops. With a few assumptions and no regenerative braking, he estimates that the crossover from one dominating to the other occurs when the distance between stops is about 750 m (~0.5 mile).
Summary
Taylor ignores rolling resistance in this chapter, so for objects immersed in a 'fluid', we can say:
At high speeds, turbulent flow and $f(v)\propto v^2$
At low speeds, laminar flow and $f(v)\propto v$
Homework
Image credits
Michael Belisle, Kraaiennest, BoH, Beck and Collins, http://www.flickr.com/photos/bike/ ( CC BY-SA 2.0)
