Linear resistance [2.2, 2.3]

Linear resistance

We can neglect the quadratic contribution to air resistance at low Reynolds number, when speeds are slow, and/or viscosity is high. $$\myv{f}(v) \approx -bv \uv{v}$$

The equation of motion for our particle is then $$m \ddot{\myv{r}} = m \myv{g} - b \myv{v}$$

Since $\dot{\myv{r}}=\myv{v}$, we can turn this into a differential equation for velocity: $$m \dot{\myv{v}} = m \myv{g} -b \myv{v}$$

We can write two scalar differential equations, one for the horizontal ($x$) component of $\myv v$, and one for the vertical ($y$) component. Following Taylor's convention, we'll say that "down" is the positive $y$-direction: $$ m \dot{v}_x = -bv_x$$ $$ m \dot{v}_y = mg -b v_y$$ Each of these is a first order differential equation which can be separated in Cartesian coordinates, and then integrated.

Horizontal motion

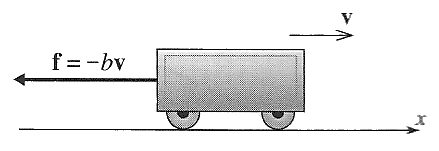The $x$ equation alone might describe a cart (with no rolling resistance!) moving over a flat surface, through a viscous medium. $$ \dot{v}_x = -\frac{b}{m} v_x$$

The exponential function has the property that its derivative is identical to itself, to within a constant of multiplication, and so the solution is: $$v_x(t)= A e^{-t b/m}=v_x(0)e^{-t/\tau}; \ \ \tau=m/b$$ As an example, below is a graph of $v_x(t)=10e^{-t/4.5}$; $10/e=3.68$)
[For a function $f(t)=Ae^{-t/\tau}$, it is useful to think of $\tau$ as the "relaxation time": the time it takes for the function to drop to the fraction $1/e$ of its starting value. Well, any starting value...]

Horizontal position, $x(t)$

The horizontal speed is: $$v_x(t)= v_{x0}e^{-t/\tau}$$ Writing $v_x=\dot x(t)=v_{x0}e^{-t/\tau}$, we have a diff. eq. for $x(t)$. Separating variables and integrating to find $x(t)$: $$\begineq x(t)&=& x(0)+\int_0^t v_x(0)e^{-t'/\tau} dt' \\ & =& 0 + [-v_x(0)\tau e^{-(t'/\tau)}]_0^t\\ & =& v_{x0}\tau (1-e^{-t/\tau}).\endeq$$

As $t \to \infty$ the bracket $(1-e^{-t/\tau}) \to 1$, so the particle will come to rest at position $x(t\to\infty)=v_{x0} \tau$.

Vertical motion

The equation for vertical motion alone might apply to something like a small droplet in a viscous medium. $$ \dot{v}_y = g -\frac{b}{m} v_y$$

Assuming that $\lim_{t \to \infty}\dot{v}_y=0$, we can solve for a terminal velocity: $$v_{\text{ter}} = \frac{mg}{b}$$

Our differential equation for $v_y(t)$ can be re-written: $$ \dot{v}_y = -\frac{b}{m} (v_y - v_{\text{ter}})$$

Hmmm. Looks just about exactly like the horizontal case. If only the time derivative of the quantity in () on the right had the same derivative on the left.

Hey wait! Since $v_{\text{ter}}$ is a constant, its time derivative is zero, and so if we defined $u(t) = v_y(t)-v_{\text{ter}}$, we indeed have $\dot{u} = \dot{v}_y$, so this looks exactly like our earlier situation: $$\dot{u} = -\frac{b}{m} u$$

The solution is: $$A e^{-t/\tau} = u(t) =v_y(t) -v_{\text{ter}}$$

We find $A$ by setting $t=0$ in the equation above: $$A \equiv v_{y0}-v_{\text{ter}}.$$

And now we can get rid of $u$ and solve for $v_y(t)$: $$v_y(t) = v_{y0}e^{-t/\tau} + v_{\text{ter}}(1-e^{-t/\tau})$$

Problem 2.5

What if a raindrop is 'thrown' downwards with an initial speed twice its terminal velocity $v_{y0} = 2v_{\text{ter}}$? Describe and graph the velocity.

Using our just-derived expression for velocity as a function of time: $$\begineq v_y(t) &= v_{y0}e^{-t/\tau} + v_{\text{ter}}(1-e^{-t/\tau})\\ &=2v_{\text{ter}}e^{-t/\tau} + v_{\text{ter}}(1-e^{-t/\tau})&=v_{\text{ter}} (1+e^{-t/\tau})\endeq$$