Central Forces
- Definition of a central force.
- Spherical-polar coordinates.
- The gradient, $\myv \grad U$, in spherical polar coordinates(!)
- Conservative forces in spherical-polar coordinates.
Consider some "thing" (maybe a charge, maybe a hunk of matter) at the origin exerting a force on an object at position $\myv r=r\,\uv r$.
The force is a central force if it can be written as: $$\myv{F}(\myv{ r}) = f(\myv{r}) \uv{r}.$$ The force acts along the line that connects the "thing" and the object.
A central force is spherically symmetric if the magnitude of the force depends only on the magnitude $|\myv{r}| = r$, that is... $$\myv{F}(\myv{r}) = f(r) \uv{r}$$
Spherical polar coordinates

If $r$ were the radius of the earth,
- $\phi$ would be the longitude relative to the prime meridian, and
- $\theta$ would be (in the Northern hemisphere) 90 deg minus the latitude.
Convince yourself of these conversions: $$x = r \sin \theta \cos \phi;\ \ y=r \sin \theta \sin \phi ;\ \ z= r \cos \theta .$$
Unit vectors
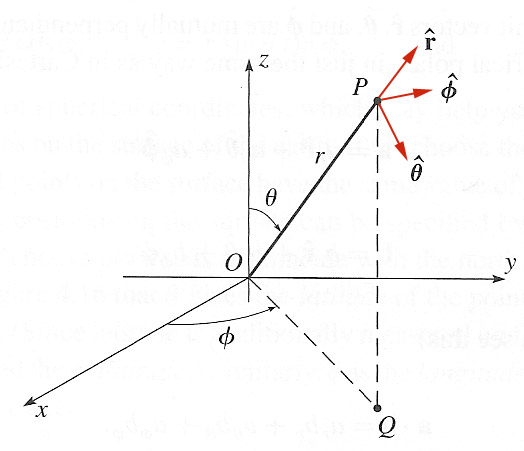
The unit vectors vary with position :-<.
But, they are mutually perpendicular. If there are two vectors, given in terms of these unit vectors at the same position, such that $$\myv{a} = a_r \uv{r} + a_{\theta} \uv{\theta} + a_{\phi} \uv{\phi}\ \text{and}\ \myv{b} = b_r \uv{r} + b_{\theta} \uv{\theta} + b_{\phi} \uv{\phi} $$
...then we can calculate their dot product as $$\myv{a} \cdot \myv{b} = a_r b_r + a_{\theta} b_{\theta} + a_{\phi} b_{\phi}$$
Change in position

The position vector $\myv{r}$ is the vector $OP$ in the figure above. Now, if $r$ changes by $dr$, $\theta$ by $d \theta $, and $\phi$ by $d\phi$, what is the change $d \myv{r}$ of $\myv{r}$? $$d \myv{r}= dr\, \uv{r} +r d \theta \,\uv{\theta} + r \sin \theta d \phi \, \uv{\phi}$$
Gradient in spherical polar coordinates
How to write the gradient in spherical coordinates?!?
We had this general expression: $$df = \myv{\grad} f \cdot d\myv{r}$$
Using the expression we just came up with for $d \myv{r}$ and the (simple) way dot products work [at a common location] in spherical coordinates we can write this in terms of the as-yet-unknown components of our gradient: $$df = (\myv{\grad} f)_r dr + (\myv{\grad} f)_{\theta} r d \theta + (\myv{\grad} f)_{\phi} r \sin \theta d\phi$$
On the other hand, for any function of three variables, we can write a small change in the value of the function as... $$df = \frac{\del f}{\del r} dr + \frac{\del f}{\del \theta} d \theta +\frac{\del f}{\del \phi} d \phi$$
Comparing these two, it looks like... $$(\myv{\grad} f)_r= \frac{\del f}{\del r};\ \ (\myv{\grad} f)_{\theta}= \frac{1}{r}\frac{\del f}{\del \theta};\ \ (\myv{\grad} f)_\phi= \frac{1}{r \sin \theta } \frac{\del f}{\del \phi }$$
Or, putting this all together in one vector expression: $$\myv{\grad} f = \uv{r} \frac{\del f}{\del r} + \uv{\theta} \frac{1}{r}\frac{\del f}{\del \theta} + \uv{\phi} \frac{1}{r \sin \theta} \frac{\del f}{\del \phi}.$$
Conservative, Central forces

[Richard Lugar was Indiana's conservative, centrist U.S. Senator...]
But, back to Physics....
If a central forces - $\myv{F} (\myv{r}) = f(\myv{r}) \uv{r}$ - is conservative then we can draw some further conclusions...
In terms of spherical coordinates, we note that our expression for a central force can be written as: $$f(\myv r)\uv r = f(\myv r)\uv r + 0 \uv \theta + 0\uv \phi,$$ that is, $F_\theta = F_\phi=0$.
If a force is conservative, it must be the gradient of a potential, that is $\myv{F} (\myv{r}) = - \myv{\grad} U = -\left[ \uv{r} \frac{\del U}{\del r} + \uv{\theta} \frac{1}{r}\frac{\del U}{\del \theta} + \uv{\phi} \frac{1}{r \sin \theta} \frac{\del U}{\del \phi}\right].$
In order for the force to be central, the $\uv{\theta}$ and $\uv{\phi}$ components of the force must vanish. This is only possible if...
$\Rightarrow \frac{\del U}{\del \theta} = 0$, and $\frac{\del U}{\del \phi}=0$
So, for a conservative force, the potential energy may not depend on $\theta$ or $\phi$: $U(r, \theta , \phi ) = U(r)$. So, the potential is not merely central, but actually spherically symmetric (depends only on $r$) and so is $\myv{F}(\myv{ r}) = -\uv{r} \frac{\del U}{\del r} = \myv{F}(r)$ So, we have shown that
If a force is central and conservative, it must actually be spherically symmetric.
(4.43 b) Spherical symmetry => conservative?
Is it enough for a force to be spherically symmetric in order to be conservative?
A force is conservative if the curl vanishes, that is $\myv{\grad} \times \myv F=0$. We'll use (but not derive!) the expression for the curl in spherical coordinates.... $$\begineq \myv{\grad} \times \myv{F} =& \uv{r}\ \frac{1}{r \sin \theta}\left[\frac{\del}{\del \theta}(\sin (\theta) F_\phi) - \frac{\del}{\del \phi}F_{\theta}\right]\\ &+ \uv{\theta}\ \left[\frac{1}{r \sin \theta}\frac{\del}{\del \phi}F_r-\frac{1}{r}\frac{\del}{\del r}(r F_\phi)\right] \\ &+ \uv{\phi}\ \frac{1}{r}\left[\frac{\del}{\del r}(rF_{\theta})-\frac{\del}{\del \theta}F_r\right].\endeq$$
First we note that $F_{\theta}=0$ and $F_{\phi}=0$.
Then, the only remaining terms involving $\frac{\del}{\del \theta } F_r$ and $\frac{\del}{\del \phi} F_r$. But these vanish since for spherical symmetry $F_r = F_r(r)$ is only a function of $r$.
So, the curl vanishes, and this means that all spherically symmetric central forces are conservative.
Homework
Chapter 4: 41, 42