Energy of interacting particles
So far we have only considered the kinetic and the potential energy of a single particle influenced by forces.
But we know of many situations (solar systems, plasma of charged particles) where each and every particle is both subject to the forces of other particles, and is itself a source of forces on the other particles.
Is there any hope of defining something like a total kinetic energy, a total potential energy, and their sum as some sort of total energy? (It would be nice if that was conserved...)
It does seem like the kinetic energy of a particle only depends on its own speed, and not on the speed of other particles, so we might start with two particles, and guess that... $$E \stackrel{?}{=} T_1(\dot{r}_1)+T_2(\dot{r}_2) + U_1(\myv r_1, \myv r_2)+U_2(\myv r_1, \myv r_2).$$ but those potential energy terms seem like they're going to get very complex very fast.
But both the gravitational force and the electrical force are central, spherically symmetric-- and $\Rightarrow$ conservative--forces. I'd like to show you that the total energy of two particles under these circumstances has a simpler form:
The total energy of two particles interacting via a central, conservative force can be written as $$E = T_1 + T_2 + U(\myv r_1 - \myv r_2)$$ Total energy is constant, and is the sum of the kinetic energies of the individual particles, and just one potential energy function that depends on a very particular combination of the two positions of the particles: their relative position = $\myv r_1-\myv r_2$.
If we have just two particles in a universe, interacting, let's write the force that particle 2 exerts on particle 1 as: $\myv{F}_{12} = \myv{F}_{12}(\myv{r}_1, \myv{r}_2)$,
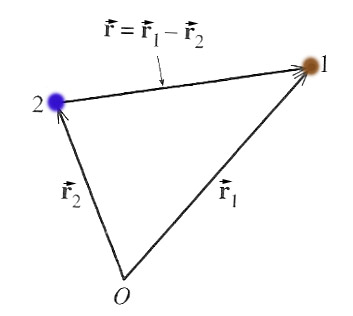 For a number of forces we are familiar with, the force only depends on the relative coordinates of the two particles. That is, the particular combination $\myv r_1-\myv r_2$:
$\myv{F}_{12} = \myv{F}_{12}(\myv{r}_1 - \myv{r}_2)$.
For a number of forces we are familiar with, the force only depends on the relative coordinates of the two particles. That is, the particular combination $\myv r_1-\myv r_2$:
$\myv{F}_{12} = \myv{F}_{12}(\myv{r}_1 - \myv{r}_2)$.
So, for example, if we are looking at the electrical force between two charges, it can be written as: $$\myv{F}_{12} = -k \frac{q_1 q_2}{|\myv{r}_1 - \myv{r}_2|^3} (\myv{r}_1 - \myv{r}_2)$$
The fact that the force only depends on the relative coordinates can be seen as a consequence of the "translational invariance of space": That is, if we change both $\myv r_1$ and $\myv r_2$ by the same amount, we expect the force to remain unchanged.
Potential energy
If the force is conservative, then we should find that the force on particle 1 depends on the gradient "$\myv{\grad}_1$" of a potential energy function, $U$, with respect to variations of the position of particle 1: $$\myv{\grad}_1 = \uv{x} \frac{\del}{\del x_1}+ \uv{y} \frac{\del}{\del y_1}+\uv{z} \frac{\del}{\del z_1}.$$
Specifically, if the force acting on particle 1 $F_{12}$ is conservative, then we can define the force as the negative gradient of a potential energy function depending on $\myv{r}_1$, $\myv{F}_{12}= - \myv{\grad}_1 U(\myv{r}_1)$,
But since $\myv\grad_1$ only cares about variations in $\myv r_1$, we could shift the origin of the potential energy by a vector, say, $\myv r_2$, and it wouldn't change the gradient of the potential: $\myv{F}_{12}= -\myv{\grad}_1 U(\myv{r}_1 - \myv{r}_2)$.
This is like saying, "Whether the gravitational potential is $U(h)=mgh$ or $U'(h)=mg(h+13.71634)$, we'll still get a force (-gradient of PE) of $-mg\uv z$."
Now consider what happens if $U(\myv r_1,\myv r_2)=U(\myv r_1-\myv r_2)$ were a function of the relative coordinates of the two particles. What happens when we take the gradient, $\myv{\grad}_2$ of this potential energy function?
Applying the chain rule, consider the partial derivatives with respect to $x_1$ and $x_2$ of the potential energy, if it depends only on $\myv r_1-\myv r_2=(x_1-x_2)\uv x+(y_1-y_2)\uv y+(z_1-z_2)\uv z$. $$\frac{\del U(\myv r_1-\myv r_2)}{\del x_1}= \frac{\del U(\myv r_1-\myv r_2)}{\del (\myv r_1-\myv r_2)}\frac{\del (x_1-x_2)}{\del x_1}\uv x=\frac{\del U(\myv r_1-\myv r_2)}{\del (\myv r_1-\myv r_2)}\uv x*(+1)$$ $$\frac{\del U(\myv r_1-\myv r_2)}{\del x_2}= \frac{\del U(\myv r_1-\myv r_2)}{\del (\myv r_1-\myv r_2)}\frac{\del (x_1-x_2)}{\del x_2}\uv x=\frac{\del U(\myv r_1-\myv r_2)}{\del (\myv r_1-\myv r_2)}\uv x*(-1)$$ The conclusion is that $\frac{\del U(\myv r_1-\myv r_2)}{\del x_1}=-\frac{\del U(\myv r_1-\myv r_2)}{\del x_2}$, and similarly for the other pairs of $y$ and $z$ variables, and therefore, indeed for the gradients.
This means that $$\myv{F}_{21} = - \myv{\grad}_2 U(\myv{r}_1 - \myv{r}_2) = \myv{\grad}_1 U(\myv{r}_1-\myv{r}_2) = -\myv{F}_{12}$$ which is Newton's third law about equal and opposite forces, which we sure wanted to have work out anyway!
If we choose as our potential energy function, $U(\myv r_1-\myv r_2)$, then Newton's 3rd law (equal and opposite reaction forces) must necessarily result as a consequence, with just that one potential energy function (a function of the relative coordinates). We don't need to have a different $U$ for each particle.
Total energy
The total energy of the system would then be $$E=T_1 + T_2 + U(\myv{r}_1 - \myv{r}_2)$$
Where $U$ takes into account in one expression the potential energy of both particles.
Interaction of many particles
I'll just state the result of section 4.10, that
(the net force on particle $\alpha$) is $-\myv{\grad}_{\alpha} U$
where $U$ is a sum of potential energies from different kinds of interactions.
Examples
Problems 4.46, 4.47
4.46: Using momentum conservation, $$m_1\myv v_1=m_1\myv v_1'+m_2\myv v_2'.$$ Square both sides: $$m_1^2 v_1^2= m_1^2v_1'^2+m_2^2v_2'^2+2m_1m_2\myv v_1'\cdot\myv v_2'.$$ Now use energy conservation to simplify this further, and solve for the dot product $\myv v_1'\cdot\myv v_2'$ to continue the problem...
4.47: Write out the equations that express energy conservation ($T_o=T_f$) and conservation of momentum ($P_o=P_f$). This gives you two equations in six unknowns: $m_1, m_2, v_1, v_1', v_2, v_2'$. This should be enough, theoretically, to eliminate two of the unknowns ($m_1$ and $m_2$) and end up with the desired relationship as an equation between the remaining four unknown speeds.