Driven oscillator

$$\begineq ma=&F\\ m \ddot{x}=& -kx - b \dot{x} \color{blue}{ + F(t)} \endeq$$

$F(t)$ is a driving force, a function of time $t$. We can again, divide the equation of motion by $m$, define $f(t) = F(t)/m$, and use those previously defined constants $\beta=b/2m$ and $\omega_0^2=k/m$ to write this as:

$$\frac{d^2}{dt^2}x + 2 \beta \frac{d}{dt}x +\omega_0^2 x = f(t).$$ Wolfram Oscillator

Sinusoidal driving force

Instead of considering all possible functions of time, let's specialize just a bit to the case of sinusoidal oscillations. Since we're going to be taking derivatives, the bookkeeping is simpler if we write a typical sinusoidal driving force as $$f(t) = f_0 e^{i\omega t}$$

• Though $f(t)$ is complex, we'll just take the real part of this (thanks to Euler's equation) when all is said and done.
• We'll assume $f_0$ is real without loss of generality: We'll eventually calculate a phase shift, $\delta$, of the oscillater response *relative* to the driving force.
• While a sinusoidal function might seem like a rather narrow solution, we will eventually find that a sum of such sinusoidal driving forces can be uniquely chosen to represent any periodic $f(t)$, as well as a single driving "pulse". So this is a step on the way to much more general time-dependent driving functions.

The differential equation for position that we would like to solve (written as a complex function of time $z(t)$) is... $$\frac{d^2}{dt^2}z + 2 \beta \frac{d}{dt}z +\omega_0^2 z = f(t).$$

What to guess?

Let us suppose that if we are driving this spring system sinusoidally at a frequency $\omega$, that its motion will eventually have the same frequency, though with an unknown amplitude and phase shift relative to the driving force. That is, our guess is (writing this as $z$ instead of $x$ to remind us that it's complex...): $$z(t)=Ce^{i\omega t} = Ae^{-i \delta}e^{i \omega t}$$

Where $C$ is the complex amplitude, but $A$ is a real number $A=\sqrt{C^*C}$. Where "$C^*C$" does not mean "C times C". It means "The complex conjugate of C times C" which is guaranteed to be a positive, real number.

Actually, our proposed solution is just the real part of $z(t)$, which is... $$Re(z(t)) = A \cos (\omega t - \delta)$$

Substituting $z(t)$ into our differential equation yields... $$-\omega^2Ce^{i\omega t} + i \omega 2 \beta Ce^{i\omega t} +\omega_0^2 Ce^{i\omega t} = f_0 e^{i\omega t}.$$

Dividing through by $e^{i\omega t}$ we get this 'auxiliary' equation for $C$: $$(-\omega^2 + i \omega 2 \beta +\omega_0^2 )C = f_0.$$ We're left with an equation that can be solved for the complex amplitude $C$, $$C= \frac{f_0}{\omega_0^2-\omega^2+2i\beta\omega}.$$

The amplitude $A$ for our real solution is $A=\sqrt{C^*C}$ which gives... $$\begineq A^2 = C^* C & = & \frac{f_0}{\omega_0^2-\omega^2-2i\beta\omega} \times \frac{f_0}{\omega_0^2-\omega^2+2i\beta\omega}\\ & = & \frac{f_0^2}{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2}\endeq$$

and therefore...

$$A= \left[\frac{f_0^2}{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2}\right]^{1/2} $$

We'd also like an expression for the phase difference $\delta$ between the driving force and the response. By substituting $C=Ae^{-i\delta}$ into our auxiliary equation for $C$ we can re-write that as: $$f_0 e^{i \delta} = A(\omega_0^2-\omega^2 + 2i\beta\omega)\label{aux}$$

Now, $f_0$ and $A$ are both real, so the phases of the complex numbers which they multiply must be the same. (Draw a picture of two vectors in the complex plane!). In terms of the complex number, in the parentheses(...) on the right side of Eq (\ref{aux})...

$$\delta = \arctan\left[\frac{\text{Im}(...)}{\text{Re}(...)}\right]=\arctan\left[\frac{2\beta\omega}{\omega_0^2-\omega^2}\right].$$

A partial solution

Now, we have the solution in hand for a sinusoidal driving force. It's the real part of $z(t)$ which is... $$x(t) = A \cos ( \omega t - \delta)$$

with the amplitude $A$ and phase offset from the driving force $\delta$ above.

But further consideration reveals that this is not the only solution...

Linear operators

Consider a function $x(t)$ and a constant $a$...

A linear operator $\hat D$ is one that has these two properties: $$\hat D(ax) = a\hat Dx;\ \ \hat D(x_1 +x_2) = \hat D x_1 + \hat D x_2.$$

Certainly the operator that represents multiplication by a constant, $k$, that is $\hat D \equiv k \times $, obeys these two properties.

Another one is $\hat D = \frac{d}{dt}$, that is, the operation of "taking the derivative with respect to $t$ ". For certainly $\frac{d}{dt} ax = a \frac{d}{dt}x$ and $\frac{d}{dt}(x_1 + x_2)=\frac{d}{dt}x_1 + \frac{d}{dt}x_2$. Higher order derivatives will also have these two properties.

Indeed, we can write the differential equation for the unforced oscillator in terms of an operator which consists of taking derivatives, multiplying by constants and adding such operations together: $$\hat{D}\equiv\frac{d^2}{dt^2} + 2 \beta \frac{d}{dt} +\omega_0^2.$$ which is a sum of products of individually linear operators. Such a combination is also a linear operator.

The differential equation that we solved for the damped (unforced) oscillator can be written in terms of this operator as... $$\hat{D}x = 0=\frac{d^2}{dt^2}x + 2 \beta \frac{d}{dt}x +\omega_0^2 x.$$

And now, the fact that this is a linear operator means that.... $$\hat{D}(ax_1 + bx_2)= a\hat{D}x_1 + b\hat{D}x_2$$

which says that, if $x_1$ and $x_2$ are solutions of $\hat{D}x = 0$, then so is $ax_1 + bx_2$.

The equation for the forced oscillator is of the form $\hat{D}x = f(t)$.

Because of the linearity of this operator, we can say that,

• if $x_h$ is a solution of what we'll call the "homogeneous" equation $\hat{Dx} = 0$,
• and $x_p$ is a 'particular' solution to our the full, forced oscillator equation $\hat{D}x = f(t)$,

Then $ax_h + bx_p$ is also a solution, since: $$\hat{D}(x_h+x_p) = \hat{D}x_h + \hat{D}x_p = 0 + f(t)=f(t)$$

In the material on the unforced oscillator, we saw that all of the solutions for the unforced oscillator for which the damping parameter $\beta > 0$ died away after a characteristic time $\tau$. So we might write the solutions for the unforced oscillator as "transient" ones of the form $x_h(t) = e^{-t/\tau}x_{tr}(t)$, and so the most general solution to the oscillator being driven by a sinusoidal force is....

$$x(t) = A \cos (\omega t - \delta) + e^{-t/\tau}x_{tr}(t)$$

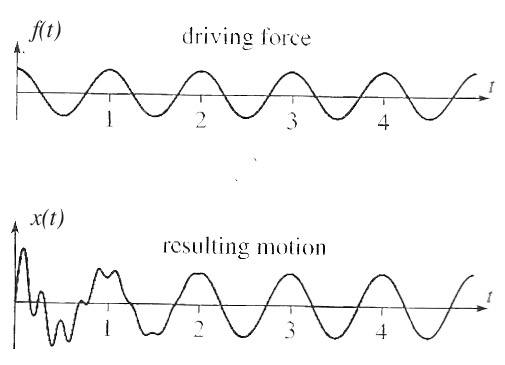
• The boundary conditions for our problem will determine the transient solution, but do not influence the long-time solution.
• No matter the initial conditions, eventually the transient solution dies off, and the system settles into the long-time behavior, $A\cos(\omega t - \delta)$. It's as if all initial conditions are "attracted" towards this long time solution. So the long time solution is called an attractor.

Homework

chapter 5:33, 35 (a & c), 38.