Resonance

LRC circuits

For the circuit shown, the current $I(t)$ flowing is related to the charge $q(t)$ (on the left side of the capacitor) by $I = \dot{q}$

There is a voltage drop (or increase) across each of the three circuit elements:

$V_C = q/C$

$V_R = IR = \dot{q} R$

$V_L= \dot{I} L = \ddot{q} L$

If we make a complete tour around the circuit, then the voltage should be the same as when we started. That is to say the sum of the three voltage drops should be 0: $V_L + V_R + V_C = 0 =L\ddot{q} +R \dot{q} + \frac{1}{C}q$

Where

• $R\dot{q}$ - (like $-b\dot x$) Resistance results in current-dependent energy loss to heat (energy dissipation).
• $(1/C) q $ - (like $k x$) a spring like element, "pushing" the system towards equilibrium,
• $L \ddot q$ - (like $m\ddot x$) Inductance is resistance to change, like inertia. But unlike friction (also a resistance to change) without loss of energy.

This equation looks very much like the differential equation we solved for the damped oscillator.

We could attach some source (might be the input from an antenna....) of EMF that is oscillating in time, ${\cal E}(t)$. This time, as we sum voltage changes around the circuit, instead of zero we get...

$L\ddot{q} +R \dot{q} + \frac{1}{C}q = {\cal E}(t)$

Amplitude of driven oscillations

Back to our mechanical, driven oscillator... $A= \left[\frac{f_0^2}{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2}\right]^{1/2}$

$A \propto f_0$.

Looking at the denominator, how do we make it very small ($\Rightarrow$ large $A$)?

It's easier to make it smaller when $\beta$ is small (compared to $\omega$ or $\omega_0$) though non-zero.

In the figure, the values of $\beta$ from top to bottom are:
0.1
0.2
0.3,
And the gray line is at $\omega=\omega_0$.

To find the value of $\omega$ that minimizes the denominator, solve

$\frac{d}{d\omega} \left[\frac{f_0^2}{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2}\right]=0$

This works out to... $\omega = \sqrt{\omega_0^2 - 2 \beta^2}$

It looks like, particularly for small $\beta$ values, that the largest amplitudes will occur when $\omega \approx \omega_0$, and that gives us this approximate value for the maximum amplitude: $A_{max} \approx \frac{f_0}{2\beta \omega_0}$

5.41 - Width of resonance peak

The width of a peak is typically characterized by its full width at half maximum (FWHM). Let's find the FWHM (problem 5.41) for the graph of $A^2$: $\frac{f_0^2}{(\omega_0^2-\omega^2)^2+4\beta^2\omega^2}$

First, let's assume that $\beta \ll \omega_0$, so that the maximum is very nearly $\omega \approx \omega_0$. For this value of $\omega$, the denominator is $4\beta^2\omega_0^2$.

So, we need to find the value of $\omega$ for which the denominator is $\color{blue}8\color{black}\beta^2\omega_0^2$, that is... $$\begineq [\omega_0^2-\omega^2]^2 =& 4\beta^2\omega_0^2\\ \left[ (\omega_0+\omega )(\omega_0-\omega ) \right]^2 =& 4\beta^2\omega_0^2 \endeq $$

Now, $\omega$ and $\omega_0$ are close enough that we might assume that $\omega + \omega_0 \approx 2 \omega_0$ (though still $\omega - \omega_0 \neq 0 $), so... $$\begineq [2\omega_0(\omega_0-\omega)]^2 \approx & 4\beta^2\omega_0^2\\ 4\omega_0^2[(\omega_0-\omega)]^2 \approx & 4\omega_0^2\beta^2 \endeq$$ $$\Rightarrow \omega_0-\omega = \pm \beta$$

Quality factor

Another way that is sometimes useful to characterize the resonance is with a "quality factor" $Q$ which is the distance from $\omega=0$ of the resonance divided by its width: $Q=\frac{\omega_0}{2 \beta}$

This turns out to be $\pi$ times the number of cycles that this underdamped oscillator would make during its characteristic decay time.

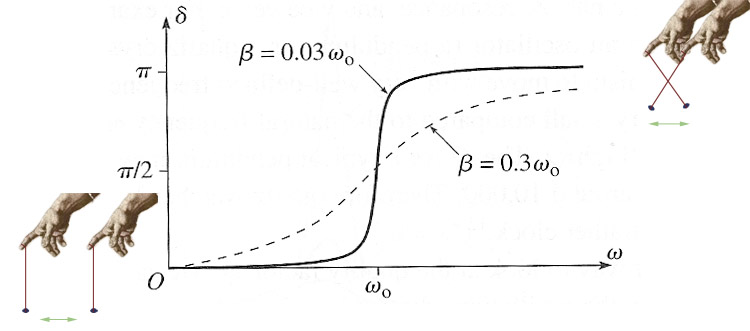
Phase change

How is the phase changing as you sweep $\omega$ through resonance? As a function of $\omega$: $$\delta(\omega) = \tan^{-1}\left(\frac{2\beta\omega}{\omega_0^2-\omega^2}\right).$$

Here's a graph of $\tan(\delta)$ as a function of $\omega$.

 

Comparing the graph of $\tan \delta$ to this one of $\tan \theta $, it looks like the phase angle $\delta$ is...

• $\approx 0$ for small $\omega$,
• $\pi/2$ at resonance ($\omega_0$),
• $\rightarrow \pi$ for $\omega \gg \omega_0$.

Homework

Chapter 5: 43, 49