Fourier series

Periodic functions

A function which repeats with "period" $\tau$: $$f(t+\tau) = f(t)$$

The sine and cosine function are periodic. In fact, there are a bunch of different ones that all have the same period:

The angular frequency, the number of "radians per second" can be expressed as $\omega=2\pi/\tau$ in terms of the period. You should convince yourself that all of these functions share a common period $\tau$: $\cos(n\omega t)$ and $\sin(n\omega t)$ where [n=0,1,2,...]

The constant function, $f(t)=C$, is periodic for all values of $\tau$>, because $f(t+\tau)=f(t)=C$. We might perversely write this as a cosine function with $\omega=0$: $$f(t)=C\cos(0 t).$$

An amazing discovery

... by Jean Baptiste Fourier (1768-1830) was that any possible periodic function can be written as a linear combination of the sine and cosine functions above:

$$f(t) = a_0 +\sum_{n=1}^{\infty}[a_n \cos (n\omega t) + b_n \sin (n\omega t)]$$

I could, somewhat perversely, write this as $$f(t) = a_0\cos(0\omega t) +\sum_{n=1}^{\infty}[a_n \cos (n\omega t) + b_n \sin (n\omega t)]$$ to emphasize the connection of all the terms to particular functions of sine and cosine.

The coefficients ($n>0$) are given by: $$a_n=\frac{2}{\tau}\int_{-\tau/2}^{\tau/2} f(t) \cos (n\omega t) \,dt,$$ $$b_n=\frac{2}{\tau}\int_{-\tau/2}^{\tau/2} f(t) \sin (n\omega t)\,dt,$$ and $$a_0 = \frac{1}{\tau} \int_{-\tau/2}^{\tau/2} f(t) \,dt = \langle f \rangle.$$ $a_0$ is the average value of the function, over one period of oscillation.

Fourier components of a square wave

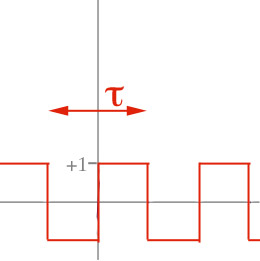We'd like to find the fourier coefficients for the square wave $f(t)$ pictured at right, where

$f(t)= +1$ for $0 < t < \tau/2$

$f(t)=-1$ for $-\tau/2 < t < 0$

The average value of the function over one period is 0, $$\Rightarrow a_0=0.$$

The cosine coefficients are: $$a_n=\frac{2}{\tau}\int_{-\tau/2}^{\tau/2} f(t) \cos (n\omega t) \,dt$$ Note that:

• $f(t)$ is an odd function, that is, $f(-t)=-f(t)$
• But the cosine is even, that is, $\cos(n\omega (-t)) =\cos(n\omega t)$,
• The product of an even function and and odd function is an odd function.
• The integral of an odd function over an even interval is zero.

$$\Rightarrow a_n=0.$$

The sine coefficients are: $$ b_n=\frac{2}{\tau}\int_{-\tau/2}^{\tau/2} f(t) \sin (n\omega t)\,dt.$$

• Both $\sin(n\omega t)$ and $f(t)$ are odd in $t$.
• An odd times an odd function = even function.
• An even function integrated over the even interval $[-\tau/2,+\tau/2]$, is twice the function integrated over the interval $[0,+\tau/2]$.
• $\omega = \frac{2\pi}{\tau}$, so $\omega\tau = 2\pi$.

$$\begineq b_n=&\frac{4}{\tau}\int_{0}^{\tau/2} f(t) \sin (n\omega t)\,dt\\ =&\frac{4}{\tau}\int_{0}^{\tau/2} 1\cdot \sin (n\omega t)\,dt\\ =&\frac{4}{\tau}\left[ \frac{-1}{n\omega} \cos (n\omega t)\,dt \right]_{0}^{\tau/2} =\frac{4}{2 \pi \tau n}\left[ \cos (n\omega \tau/2)+1 \right] \\ =&\frac{4}{2 \pi \tau}\left[ \cos (n\pi)+1 \right] \endeq $$ The quantity in square brackets [...] is 2 if $n$ is odd, and 0 if $n$ is even, so... $$\Rightarrow b_n= \left\{ \begin{matrix} \frac{4}{\pi n} & n \text{ odd}\\ 0 & n \text{ even}\end{matrix} \right. $$

So, the fourier series for $f(t)$ should be $$f(t) = +\frac{4}{\pi}[\sin(\omega t) +\frac{1}{3}\sin(3\omega t)+\frac{1}{5}\sin(5\omega t)+\frac{1}{7}\sin(7\omega t)+...]$$

The graph shows $f(t)$ with successively more of the terms above, and shifted vertically (except for the lowest graph) so as to see each function separately.

one term,
three terms,
5 terms,
11 terms.

Homework

Chapter 5: 47