Finding the best path

Fushimi Inari, Kyoto, Japan, by Agustin Rafael Reyes
The Euler-Lagrange equation
The general problem is to minimize some expression $S$, given in terms of an integral, like $$S=\int_{x_1}^{x_2} f[y(x), y'(x), x]\,dx.$$
Think of $f(x)$ as an "accounting" function: It tells us *how* to calculate the "thing to be minimized" for some particular path, $y(x)$. The choices for this "accounting function" that we saw so far, are:
- Minimize the distance travelled: This means minimize $ds$ for a particular path. To write this in terms of an integral of $f(y,y',x)$ as above, notice that... $$\begineq ds =&\sqrt{ds^2}=\sqrt{dx^2+dy^2}=\sqrt{dx^2+(\frac{dy}{dx}dx))^2}\\ =&\sqrt{ dx^2+(\frac{dy}{dx})^2 dx^2}=\sqrt{dx^2 \left[1+ \left(\frac{dy}{dx}\right)^2\right]}\\ =&dx\sqrt{1+(y'(x))^2}\endeq$$ and so $f(y,y',x) = \sqrt{1+(y')^2}$.
- Minimize the time (Fermat's principle for light): This means that we should minimize $dt=ds/v$. In the case of light, we can write the speed of light as $v=c/n(\myv r)$, where $n$ is the index of refraction, which depends on the position.
Since we're right now looking at functions in two dimensions, let's write this as $v=c/n(x,y)$. putting this together with our expression above for $ds$, we find: $$ dt=\frac{ds}{v}= \frac{\sqrt{1+(y')^2}}{n(x,y)}dx$$ and so our "accounting function" can be written as $$f(y,y',x)=\frac{\sqrt{\color{blue}1+\color{black}(y')^2}}{n(x,y)}$$
Note that in both cases, the "accounting function", $f$, can be written as a function of $x$, $y$, and $y'$.
We need to minimize $S$ by means of an appropriate choice of function $y(x)$, where the only constraint on $y(x)$ so far is that it's a function that passes through two definite points:
$y(x_1) = y_1$ and $y(x_2)=y_2.$
Since $y(x)$ and $y'(x)$ are functions of $x$, $f[y(x),y'(x),x]$ is actually ultimately a function of $x$.
Imagine that $y(x)$ is actually the function that minimizes $S$. Then $S$ must be a bit larger when the path is slightly different from $y$--say $y(x) +\eta(x)$. Here, $\eta(x)$ is some continuous function, that is non-zero except at the endpoints (see the diagram below):
$\eta(x_1) = 0$ and $\eta(x_2) = 0$.

Or, we could parameterize things with a constant $\alpha$, where a wrong (non-minimum) path is given by $$Y(x) \equiv y(x) + \alpha \eta(x),$$ and then as $\alpha \rightarrow 0$, $Y(x) \rightarrow y(x)$.
Now $S$ depends on the parameter $\alpha$: $$S(\alpha)= \int_{x_1}^{x_2} f(Y(\alpha,x), Y'(\alpha,x),x)\,dx =\int_{x_1}^{x_2} f(y+\alpha\eta, y'+\alpha\eta',x)\,dx.$$
For *all* the functions, the prime ' means $\frac{\del}{\del x}$. In particular, $\eta'(x)=\frac{\del \eta}{\del x}$.
If $y(x)$ is the solution that minimizes $S$, then we would expect that this would be the condition for a minimum: $$\begineq \left.\frac{dS}{d\alpha}\right|^{\alpha=0}=0 =& \left[ \int_{x_1}^{x_2} \frac{\del f(Y, Y',x)}{\del \alpha}\,dx \right]^{\alpha=0}\\ =&\left[ \int_{x_1}^{x_2} \left( \frac{\del f(Y, Y',x)}{\del Y} \frac{\del Y}{\del \alpha} +\frac{\del f(Y, Y',x)}{\del Y'}\frac{\del Y'}{\del \alpha} \right) \,dx \right]^{\alpha=0}\\ \endeq$$
There are 4 terms to figure out. 2 of these are... $$\frac{\del Y}{\del \alpha} = \frac{\del (y(x)+\alpha \eta(x))}{\del \alpha} = \eta(x)$$
and $$\frac{\del Y'}{\del \alpha} = \frac{\del (y'(x)+\alpha \eta'(x))}{\del \alpha} = \eta'(x).$$
The other two will eventually be evaluated at $\alpha=0$, whence $$\left.\frac{\del f(Y, Y',x)}{\del Y}\right|^{\alpha=0}= \frac{\del f(y, y',x)}{\del y}$$ $$ \left.\frac{\del f(Y, Y',x)}{\del Y'}\right|^{\alpha=0}= \frac{\del f(y, y',x)}{\del y'}$$
Putting this all back into our minimization condition $$\begineq \frac{dS}{d\alpha} = 0 =& \int_{x_1}^{x_2}\frac{\del f}{\del \alpha}\,dx \\=& \int_{x_1}^{x_2}\left(\eta \frac{\del f}{\del y} + \eta' \frac{\del f}{\del y'}\right) dx.\endeq$$
We'll push this further by using integration by parts to re-write the last piece as... $$\begineq \int_{x_1}^{x_2}\eta'\frac{\del f}{\del y'} dx =& \left[\eta(x)\frac{\del f}{\del y'}\right]_{x_1}^{x_2} -\int_{x_1}^{x_2} \eta\frac{d}{dx}\frac{\del f}{\del y'} dx \\ =& 0 -\int_{x_1}^{x_2} \eta\frac{d}{dx}\frac{\del f}{\del y'} dx \endeq$$
The quantity in brackets $[..]$ vanished because we required $\eta(x_1)=0$ and $\eta(x_2)=0$.
Substituting into our minimization condition gives... $$\frac{dS}{d \alpha} = 0 = \int_{x_1}^{x_2}\eta(x)\(\frac{\del f}{\del y}-\frac{d}{dx}\frac{\del f}{\del y'}\)\, dx.$$
Since $\eta(x)$ could be just about any function, the only way to assure that this expression vanishes is if ....
$$\frac{\del f}{\del y}-\frac{d}{dx}\frac{\del f}{\del y'} = 0$$
This is the Euler-Lagrange equation.
So, very generally:
- As long as our "accounting function", $f$, is some function of $x$, $y(x)$, and $y'(x)$,
- The path, $y(x)$, that minimizes that integral $\int f(y,y',x)\,dx$ must satisfy the Euler-Lagrange differential equation.

We have transformed the problem of finding a path, $y(x)$ which minimizes an integral into the problem of solving a differential equation for $y(x)$!
Applications
Shortest path between two points
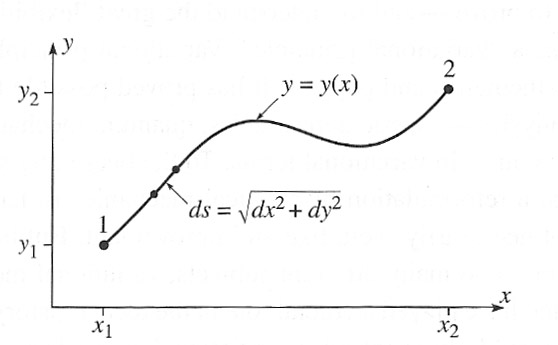
The problem was to minimize the length $L$: $$\begineq L =& \int_1^2 ds =\int_1^2 \sqrt{ds^2} = \int_1^2 \sqrt{dx^2+dy^2} = \int_1^2 \sqrt{dx^2+\left(dx\frac{dy}{dx}\right)^2 } \\ =&\int_{x_1}^{x_2} \sqrt{1+y'(x)^2} dx. \endeq $$
Solve it this way:
- identify the function $f(y,y',x)$ that appears in the integral: $$f(y,y',x)=\sqrt{1+y'(x)^2}.$$
- Write out the E-L equation $\frac{\del f}{\del
y}-\frac{d}{dx}\frac{\del f}{\del y'} = 0$ and calculate the terms:
There is no explicit dependence of $f$ on $y$ so the first term vanishes, $$\frac{\del f}{\del y}=0.$$
Work out the partial derivative in the 2nd term: $$\frac{\del f}{\del y'}=\frac{\del (1+y'^2)^{1/2}}{\del y'} = \frac 12(1+y'^2)^{-1/2}2y'=\frac{y'}{\sqrt{1+y'^2}}.$$ Putting the pieces together, the E-L equation becomes: $$\begineq \frac{\del f}{\del y}-\frac{d}{dx}\left(\frac{\del f}{\del y'}\right)=&0\\ 0-\frac{d}{dx}\left(\frac{y'}{\sqrt{1+y'^2}}\right) =& 0.\endeq$$
- Solve the E-L differential equation for $y(x)$, using any boundary conditions as needed:
The equation above implies that: $$\frac{y'}{\sqrt{1+y'^2}} = c.$$
Squaring and doing some algebra: $$\begineq \frac{y'^2}{1+y'^2} =& c^2\\ y'^2 =& c^2(1+y'^2)\\ y'^2-c^2y'^2=&c^2\\ y'^2=&\frac{c^2}{1-c^2}\equiv m^2\\ \frac{dy}{dx}=&\pm m \endeq$$
The solution to this diff eq is $$y(x)=m x + b.$$ and you can choose $m$ and $b$ to run through the two points 1 and 2.
Whaddaya know: A line is the shortest path between two points !!!
Homework
Chapter 6, problems 3,8,10.
