Using Gauss' law
We started with Gauss' theorem, which is true of any vector field:
$$\oint_{\cal S} \myv E \cdot d \myv a = \int_{\cal V} \myv \grad \cdot \myv E \,d \tau.$$
We found that the divergence of the electric field is the charge density:
$$\myv \grad \cdot \myv E = \frac{\rho}{\epsilon_0},$$
at each and every point in space.
Substituting this expression into Gauss' theorem results in what is called "Gauss' Law" in electrodynamics:
Gauss' law: $$\oint_{\cal S} \myv E \cdot d \myv a = \oint_{\cal S}d\Phi_E = q_{\text enc}/\epsilon_0.$$
Gauss' law is always true. But it's tough to calculate flux integrals for complicated surfaces.
But sometimes, when we can take advantage of symmetry, we can use Gauss' law to actually calculate the electric field exactly! As we shall now see...
Field near an infinite plane of charge
Imagine an infinite flat sheet of charge with a two-d charge density $\sigma$.
What is $\myv E$ at a height $z$ above the sheet?
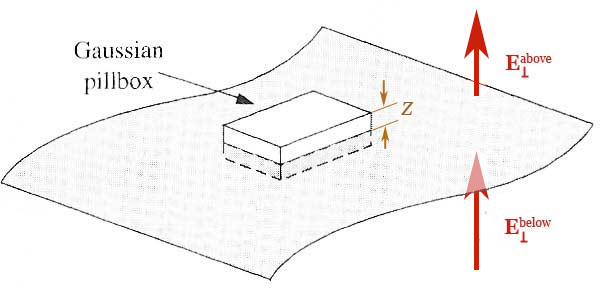
Calculating $\myv E$ near an infinite plane of charge using symmetry and Gauss' Law - Narrated: 13 min
- What is the full, vector expression for $d\myv a$ in Cartesian coordinates for the top of the box? Does this make sense to you?
On the top of the box: $$d\myv a = dx\,dy\,\uv z.$$ On the bottom of the box...Since we are interested in how much "flow" is going out of the box, we need to dot the electric field into a vector which is point to the outside of the box. So, on the bottom surface of our Gaussian box... $$d\myv a = dx\,dy\,(-\uv z).$$
- What would the full vector expression be for d$\myv a$ on the surface of a sphere, in spherical polar coordinates? ($r,\theta, \phi$)
The temptation is to look at the variables which are changing to integrated over the surface of a sphere, that is $\theta$ and $\phi$, but not $r$, and write... $$d\myv a = d\theta\,d\phi\,\uv r$$ But this cannot be right... Looking at the unit, $d\theta$ and $d\phi$ are in radians so this $d\myv a$ would have units of radians^2, whereas in Cartesian coordinates (above) $dx$ and $dy$ have units of length (meters).
The solution is to re-examine the lengths on the sides of the $d\tau$ box for S-P coordinates, back on our "Curvilinear coordinates" page... What we really want is $$d\myv a = dl_\theta\, dl_\phi\, \uv r,$$ where $dl_\theta$ means "how far does the position vector move when the angle $\theta$ changes by an amount $d\theta$". - Paul kinda glossed over what the electric field, $\myv E$, is *below* the infinite sheet. How would you write that?
We found that the magnitude of the electric field is constant everywhere, it's $|\myv E|=\frac{\sigma}{2\epsilon_0}$. But it's always pointing away from the sheet of charge. You could write this as: $$\myv E(\myv r)=\begin{cases} \frac{\sigma}{2\epsilon_0}\,\uv z&\text{ if } z\gt 0\\ -\frac{\sigma}{2\epsilon_0}\,\uv z&\text{ if } z\lt 0\end{cases} $$ Or, get fancy and write it at one go like... $$\myv E(\myv r)=\frac{\sigma}{2\epsilon_0}\,\frac{\myv z}{|\myv z|}.$$
- What "muddy points" were there for you in this video? What do you still wonder about?
By symmetry, it seems that the field can only have a $z$-component: $\myv E = E_z\uv{z}$. So, when we take the flux integral over the "pillbox" pictured, $\myv E$ and $d \myv a$ are at right angles on all the sides of the box. On the top and bottom, $\myv E \cdot \myv{a}= E_z da$ on both. Thus...
Show that, $$\begineq \oint_{\cal S} \myv E \cdot d \myv a &= q_\text{enc}/\epsilon_0\\ 2E_zA &= \frac{\sigma A}{\epsilon_0}.\endeq$$
Show that: $$E_z = \frac{\sigma}{2 \epsilon_0}.$$
The field above an infinite sheet of charge is constant--independent of height $z$!
Problem 2.7 revisited
Here was our vector integration solution to Problem 2.7 .
Find the electric field a distance $r$ away from the center of a spherical surface of radius
$R$ that has a total charge $q$ on it, spread uniformly over its surface.
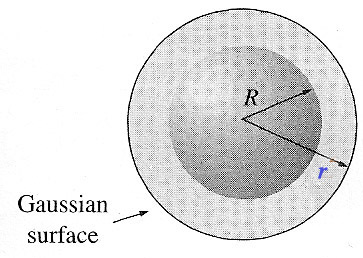
This time, imagine a second, "Gaussian" spherical surface ${\cal S}$ of radius $r$ centered on the the charged sphere.
Now we will use symmetry!: The charge is spread out with spherical symmetry. Consider a point outside of the surface. Could the field have a $\theta$ or $\phi$ component??
If not, we conclude that spherical symmetry implies that... $$\myv E(r, \theta, \phi)=E(r) \uv r.$$
Use Gauss' law, $$\oint_{\cal S} \myv E \cdot d \myv a = q_{\text enc}/\epsilon_0.$$ When $r>R$, show that this gives us... $$|E| = \frac{q}{4\pi \epsilon_0} \frac{1}{r^2}.$$
$$\oint_{\cal S} \myv E \cdot d \myv a = \oint_{\cal S} |E| da = |E| 4\pi r^2 = q/\epsilon_0.$$
If $r < R$ there is no charge enclosed by the Gaussian surface ${\cal S}$, then $E(r) = 0$.
A Gaussian cylinder, used to find the field around a line charge. Use symmetry to convince yourself that $\myv E(z,s,\phi) = E(s)\,\uv s$,

You'll find this progression:
- Spherical symmetry: Field of a point charge: $E \propto 1/z^2$,
- Cylindrical symmetry: Field of a (infinite) line charge: $E \propto 1/z$,
- Planar symmetry: Field of a (infinite) surface charge: $E = $ constant.
Problem 2.12
Find the electric field inside a sphere that has a total charge $Q$ on it, distributed uniformly, with a radius $R$. That is, it has a constant charge density of $\rho=Q/(4 \pi R^3/3)$
The field is spherically symmetric. Using Gauss' law you should find.. $$\myv E(\myv r)=\frac{Q}{4\pi \epsilon_0 R^3}\myv r.$$
Consider a spherical, Gaussian surface, of radius $r$, centered on the center of the sphere. Then the electrical field on the surface of this Gaussian surface is related to the charge enclosed by Gauss' law: $$\iint_{\cal S}\myv E\cdot d\myv a=\frac{q_\text{enclosed}}{\epsilon_0}$$ We use the spherical symmetry of the situation to surmise that the electric field at every point on the surface, ${\cal S}$ of the sphere will have the same magnitude, and point in the radial direction. And that as the radius of the Gaussian sphere changes, the electric field magnitude will change, but will not depend on $\theta$ or $\phi$. That is to say: $\myv E(r,\theta,\phi)=E(r)\uv r$. So, now we calculate (on the left) the surface integral, and (on the right) the enclosed charge: $$\begineq \iint_{\cal S}\myv E\cdot d\myv a&=\frac{q_\text{enclosed}}{\epsilon_0}\\ \iint_{\cal S}E(r)\uv r\cdot r^2\sin\theta \uv r&=\frac{1}{\epsilon_0}\iiint_{\cal V}\rho\,d\tau\\ E(r)r^2\int_{\theta=0}^\pi\int_{\phi=0}^{2\pi}\sin\theta\,d\theta\,d\phi&=\frac{\rho}{\epsilon_0}\iiint_{\cal V}d\tau\\ E(r)4\pi r^2&=\frac{\rho}{\epsilon_0}\frac 43 \pi r^3 =\frac{1}{\epsilon_0}\frac{Q}{(4/3)\pi R^3}(4/3) \pi r^3=\frac{Q}{\epsilon_0}\frac{r^3}{R^3}. \endeq $$ Solving for $E(r)$, the field is: $$\begineq\myv E=E(r)\uv r &= \frac{Q}{4\pi\epsilon_0}\frac{r^3}{r^2R^3}\uv r\\ &= \frac{Q}{4\pi\epsilon_0R^3}r\uv r = \frac{Q}{4\pi\epsilon_0R^3}\myv r. \endeq$$
For $r\gt R$, the total enclosed charge is constant, $Q$, independent of the radius, $r$, of the Gaussian sphere, and the field is
$$\myv E = \frac{1}{4\pi \epsilon_0}\frac{Q}{r^2}\uv{r}.$$
Graphing the radial component of the electric field, you should find...
$E_r$
$r$
Slightly more complicated...
Consider the field in and around two spheres, each with constant charge density
$\rho$.

Even though this problem does not have spherical symmetry, because of the principle of superposition the resulting field will be equal to the sum of the fields from the two spherically symmetric bodies, and we can use Gauss' Law to find the solution of each of those in isolation.
Summary of high symmetry cases
It is *always* true that $$\iint_{\cal S}\myv E(\myv r)\cdot d\myv a=\iiint_{\cal V}\myv \grad\cdot \myv E(\myv r)\,d\tau.$$ The surface, ${\cal S}$ is a closed "Gaussian surface" and ${\cal V}$ is the volume contained in ${\cal S}$. The right-hand side is $\frac 1{\epsilon_0}\iiint_{\cal V}\rho(\myv r)\,d\tau=Q_\text{enc}/\epsilon_0$.
Here are the most common high-symmetry cases:
| spherical symmetry | cylindrical symmetry | planar symmetry | |
|---|---|---|---|
| Charge distribution is symmetric about... | a point (the origin) | a line (the $z$ axis) | a plane ($y=0$) |
| $\myv E(\myv r)$ simplifies to... | $E(r)\uv r$ | $E(s)\uv s$ | $E(y)\uv y$ |
| Gaussian surface | a sphere of radius $r$ | a "can" of radius $s$ and length $L$ | a box (or pill box) extending from $-y$ to $+y$, with an area $A$ perpendicular to $\uv y$. |
| Flux integral $\iint \myv E\cdot d\myv a$ | $4 \pi r^2 E(r)$ | $2\pi s L E(s)$ | $2AE(y)$ |
Enclosed charge
For spherical symmetry, the enclosed charge is: $$\int_{\theta=0}^{\pi}\int_{\phi=0}^{2\pi}\int_{r'=0}^r\rho(r')r'^2\sin\theta\,dr' d\phi d\theta \\ = 4\pi\int_{r'=0}^r\rho(r')r'^2\,dr'$$
For cylindrical symmetry, the enclosed charge is: $$\int_{z=0}^L\int_{\phi=0}^{2\pi}\int_{s'=0}^s\rho(s')s'\,ds' d\phi dz\\ =2\pi L\int_{s'=0}^s\rho(s')s'\,ds'$$
Note that you *still* have to multiply the enclosed charge by $1/\epsilon_0$ before setting it equal to the flux integral, and solving for $E$.
This leads to simple formulas for each case. For example, for spherical symmetry: $$\myv E(\myv r)=\frac{1}{\epsilon_0 r^2}\int_{r'=0}^r\rho(r')r'^2dr'\,\uv r.$$