Current
- Current is charge per unit time passing a point in space.
- A flow of positive charges to the right of 1 Coulomb / sec is the same current as 1 Coulomb / sec of negative charge flowing to the left.
- 1 Coulomb / 1 sec $\equiv$ 1 Ampere = 1 A.
The current in a wire can be cartoonified as a constant line charge $\lambda$ (units: charge / length) moving with a velocity $v$. This combination $$I = \lambda v,$$ has the right dimensions for current....
But current also has a (vector) direction, so we should write: $$\myv I = \lambda \myv v.$$
The force on little chunk of charge, $dq$ that is moving in a magnetic field: $$d\myv F_m = dq\,\myv v\times\myv B.$$ Integrating to get the total force on a wire: $$\myv F_m = \int (\myv v \times \myv B) dq = \int (\myv v \times \myv B) \lambda d l = \int (\myv I \times \myv B) dl$$
For every segment of a wire, there is just as much current flow in as current flow out. Then $I$ is constant along the path of the wire. With $d\myv l$ pointing in the direction of the current... $$\myv F_m = I \int (d \myv l \times \myv B).$$
Electrostatics included: point charge $q$, line charge $\lambda$, surface charge $\sigma$, and volume charge densities $\rho$. If each of these "kinds" of charge is mobile, and moving with a velocity $\myv v$, the corresponding quantities are...
| Current-related quantity | $$\myv F_m$$ |
|---|---|
| line current $\myv I = \lambda \myv v$ | $$\int (\myv v \times \myv B) \lambda d l = \int (\myv I \times \myv B) dl$$ |
| Surface current density $\myv K = \sigma \myv v$: Current per unit width perp to flow. | $$\int (\myv v \times \myv B) \sigma da=\int (\myv K \times \myv B) da$$ |
| Volume current density $\myv J = \rho \myv v$: Current per unit area perpendicular to the flow. | $$\int(\myv v \times \myv B) \rho d \tau = \int (\myv J \times \myv B) d \tau$$ |
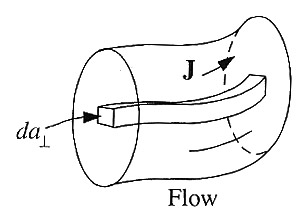So, the
current $dI$ flowing in the square-cross-section "extruded playdoh thing"
that's shown here which has a cross-sectional area $da_\perp$, in a region
where the current
density is $\myv J$,
is
$$dI = da_{\perp} J.$$
Problem 5.5.b
A current $I$ flows down a wire of radius $a$. If it's distributed in such a way that the volume current density is inversely proportional to the distance from the axis, what is $J$?
This is two conditions on $J$:
The first is that the functional form for $J$ is $J(s)=k/s$ for $0<s<a$. (And $J=0$ for $a<s$).
The second is that the total current, integrated over a cross-section through the wire is (using cylindrical coordinates): $$I = \int dI = \int J da_\perp = \int_0^{2\pi} d \phi \int_0^a s\,ds\ k/s=2 \pi k \int_0^a ds = 2\pi k a.$$
Solving this for the constant $k$, we get: $$J(s) = \frac{I}{2\pi a} \frac{1}{s}.$$
Local charge conservation
According to the problem we just did, the current crossing some surface ${\cal S}$ is $$I = \int_{\cal S} J da_\perp = \int_{\cal S} \myv J \cdot d \myv a,$$ [$d\myv a$ is a small piece of surface area, with units like "square meters", and it points in a direction perpendicular to the surface.]
If we integrate over a closed surface, we can use the divergence theorem to write the integral as a volume integral over the enclosed volume. $$\oint_{\cal S} \myv J \cdot d \myv a = \int_{\cal V} (\myv \grad \cdot \myv J) d \tau.$$
This integral must be the total charge leaving $\cal V$ in a unit of time. Since charge is conserved, that's just $-\frac{d}{dt}Q_\text{enc}$ which we can write as: $$\int_{\cal V} (\myv \grad \cdot \myv J) d \tau = -\frac{d}{dt}\int_{\cal V} \rho d \tau = - \int_{\cal V} \frac{\del \rho}{\del t} d \tau.$$
But the volume $\cal V$ is completely arbitrary, so it must be the case that:
At every point in space: $$\myv \grad \cdot \myv J = -\frac{\del \rho}{\del t}.$$ This is called the continuity equation.