Legendre transformations

Gibbs Law is this form of the first law: $$du=T\,ds-P\,dv.$$ So, we can naturally think of $u$ as being a function, $u(s,v)$, of entropy and volume. But the Pfaffian of such a function is... $$du=\frac{\del u}{\del s}ds +\frac{\del u}{\del v}\, dv.$$ If this is true, since $s$ and $v$ may be indepently varied, it must be the case that the coefficients of $ds$ in both of these equations are the same, as well as the coefficients of $dv$, which is to say: $$\left(\frac{\del u}{\del s}\right)_v \equiv T;\ \ \text{ and }\ \ \left(\frac{\del u}{\del v}\right)_s \equiv -P.$$

The enthalpy was defined as $h=u+Pv$ and so the differential of enthalpy is: $$\begineq dh&=du+P\,dv+v\,dP\\ &=(T\,ds-P\,dv)+P\,dv+v\,dP\\ &=T\,ds+v\,dP\\ \endeq$$ Apparently the enthalpy is naturally a function, $h(s,P)$, of entropy and pressure, where pressure is $-(\del u/\del v)_s$, whih is a partial derivative of $u$.

We've seen that $h$ is more useful than $u$ for constant pressure processes.

Legendre transformations

The relationship of $u=u(s,v)$ and $h=h(s,P)$ is an example of a more general problem: In what follows, $u\equiv\del f/\del x$ (not internal energy!), and $v\equiv \del f/\del y$ (not volume!).

Given a function $f=f(x,y)$ of two independent variables $x$ and $y$: $$\begin{align} df = & \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy\\ \equiv & u\,dx + v\,dy.\end{align}$$

Is there some general recipe to come up with a function $g=g(u,y)$ where...

• the independent variables of this new function are $u=\partial f/\partial x$ and $y$ instead of $x$ and $y$, and
• the function $g(u,y)$ is some composition of $f$, $x$, $y$, $u$, and $v$, and
• $g$ has the same units as $f$?

Yes! The recipe is surprisingly simple:

$$g = f - ux.$$

1. You should verify that... $$dg = v\,dy - x\,du,$$ which shows that $g=g(u,y)$...

The original definition of $v$ was $v=\frac{\partial f}{\partial y}$. But we see from this Pfaffian of $g(y,u)$ that it's also true that $v=\frac{\partial g}{\partial y}.$ Summarizing: $$v=\frac{\partial f}{\partial y} =\frac{\partial g}{\partial y}.$$

Looking at the Pfaffian, it must also be true that: $$x=-\frac{\partial g}{\partial u}.$$

Apparently, as the example of internal energy and enthalpy shows, $g=f+ux$ would also work as a Legendre transformation.

Legendre transformation of a function of 1 variable

In pictures!

Give this as an out-of-class exercise.

When $f$ is a function of just one variable, that is, $f=f(x)$, there is a nice visualization of the Legendre transformation.

The Pfaffian of a function of 1 variable, $f(x)$, is $df=(d f/d x)\,dx\equiv u\,dx$. The Legendre transformation is $$g(x)=f -ux=f(x)-\left(\frac{df}{dx}\right)_{\text{at } x}x.$$

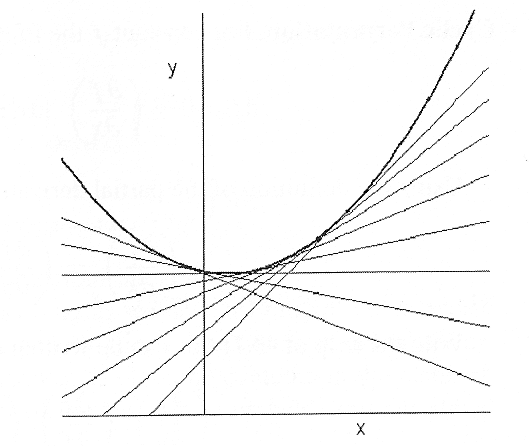
To find out graphically what the meaning of $g(x)$ is, you will carefully draw and label things on the accompanying figure:

1. Pick some particular $x$ value, and label it as '$x$' on the $x$-axis.
2. Draw a line up to meet the curve at $y=f(x)$.
3. Draw a horizontal line to the $y$-axis, and mark this height as '$f(x)$' on the $y$-axis.
4. Draw the tangent line to the function at $(x,f(x))$ that has slope $f'(x)$. Draw the line long enough to cross the $y$-axis.
5. $u\cdot x = f'(x) x$ is the change in height ($\Delta y$) of the tangent line, as you go from $0$ to $x$ in the horizontal direction. Draw a vertical line segment of length $f'(x)x$ on the diagram in a place to make the connection visually with its meaning. Label the distance '$ux$' on your line segment.
6. You have already marked $f(x)$ on the $y$-axis for the $x$ value you choose. Now find $g(x)=f(x)-ux$ visually, Mark and label that $y$ position as '$g(x)$' on the $y$-axis.

Now answer these questions or draw on the diagram as directed.

2. How would you describe the relationship of $g(x)$ to $f(x)$?
   
   
   
3. For $x=0$, what will $g(0)$ be?
   
   
4. Choose a couple of other $x$-values and find $g(x)$ for each of these values. Use these to sketch out (in another color, but on the same figure) the function $g(x)$.
5. Find algebraically the Legendre transformation $g(x)$ of the function $f(x)=3x^2-x+5$.
   
   
   
   
6. Plot with CoCalc or Desmos (or something else) the two functions $f(x)$ and $g(x)$ on the same graph. (In CoCalc you can plot( [f(x),g(x)], ...)). Print out and attach the plot: Label $f(x)$ and $g(x)$. Pick one $x$ value (not zero) and make the construction above to justify visually the value $g(x)$ for that $x$.

The Legendre transformations of internal energy

[OK, now we're back to $u\equiv$ internal energy and $v\equiv$ volume!]

Given $u(s,v)$, and its partial derivatives $T$ and $P$, we could find Legendre transformations which will be function of $s$ and $P$; $T$ and $v$; or $T$ and $P$:

	$du=T\,ds - P\,dv$	$u(s,v)$	$\partial u/\partial v = -P$ $\partial u/\partial s = T$
$h=u+Pv$	$dh = T\,ds + v\,dP$	$h(s,P)$
$f = u - Ts$	$df = -s\,dT - P\,dv$	$f(T,v)$
$g = u -Ts+Pv$	$dg=-s\,dT+v\,dP$	$g(T,P)$

You can show any of these differentials by differentiating the definition of the function, and using $du=T\,ds-P\,dv$, then simplifying.

[Pro tip for googling: A Legendre "transformation" is different from a Legendre "transform".]