
Stern-Gerlach experiments [1.1]
- Using what you know about the Lorentz force, $\myv F=q(\myv E + \myv v \times \myv B)$...
- justify the energy of a loop of current in a (constant) magnetic field: No net force on the loop, but there is a net torque on a loop.
- Creating a non-constant magnetic field results in a net force on a current loop.
- How is a spinning, charge particle (maybe an electron...?) like a current loop?
- A Stern-Gerlach magnet separates moving, charged particles according to the orientation of their "effective current loop", aka "magnetic moment".
Classical force on a current-carrying loop
The Lorentz force acting on a charge:
$$\myv F=q(\myv E + \myv v\times\myv B).$$
A video version of our demonstration of the effect of a magnetic field on beam of electrons:
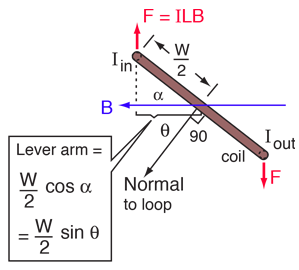
Hyperphysics: Torque on a Current Loop
Imagine that a rectangular loop of wire of dimensions $W \times L$, with a current of magnitude $I$ circulating around the loop, is positioned in a region of space where the magnetic field, $\myv B=B\uv z$, is pointing in the $\uv z$ direction, and has a constant magnitude.
- Verify that the forces are correctly oriented based on the velocity of the charge carrying particles, implied by the current flow.
- Of course, there are *two* possible directions for the "Normal to the loop". Describe a right-hand rule that selects the one pictured.
- The author of the diagram above has not drawn in any Lorentz forces acting on the near and far segments (of length $W$) of the loop... Do such forces exist? If so, what direction are those forces pointing, and why might they not be pictured?
- Estimate the net force acting on the current loop.
- Show that the units for $IL$ and $qv$ are the same...
- Show that the torque is proportional to the area enclosed by the current loop.
- What is/are the equilibrium orientations of the loop? Which are stable and which are unstable?
- Thinking in energy terms about some sort of energy related to how the loop is positioned relative to the magnetic field... describe the "ground state" (lowest possible energy state) of this loop.
Magnetic moment
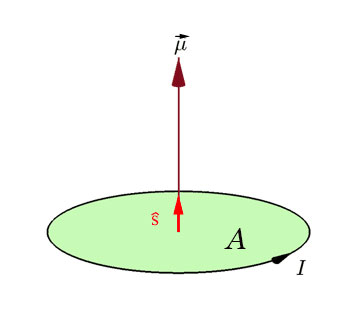 Classically, A current $I$ due to charge running in a loop in a plane with interior area $A$ has a (vector) magnetic moment $\myv{\mu}$ of
$$\myv{\mu} = IA\hat{s}.$$
Classically, A current $I$ due to charge running in a loop in a plane with interior area $A$ has a (vector) magnetic moment $\myv{\mu}$ of
$$\myv{\mu} = IA\hat{s}.$$
If current arises from a spinning particle with intrinsic angular momentum $\myv S=S \uv s$ then it should also be the case that $\myv \mu \propto \myv S$.
The considerations above will hopefully make plausible this expression for the potential energy of such a current loop in a magnetic field: $$U=- \myv{\mu}\cdot\myv{B}.$$
- What is the ground state of such a current loop? (Does this match your considerations above?)
- What is the highest energy configuration of this loop?
- What questions do you have about this expression?
A non-uniform magnetic field
We have been considering a current loop in a constant magnetic field. Now consider this configuration of magnets which produces a field pointing in the $\uv z$ direction, but getting weaker, as a $z$ increases:
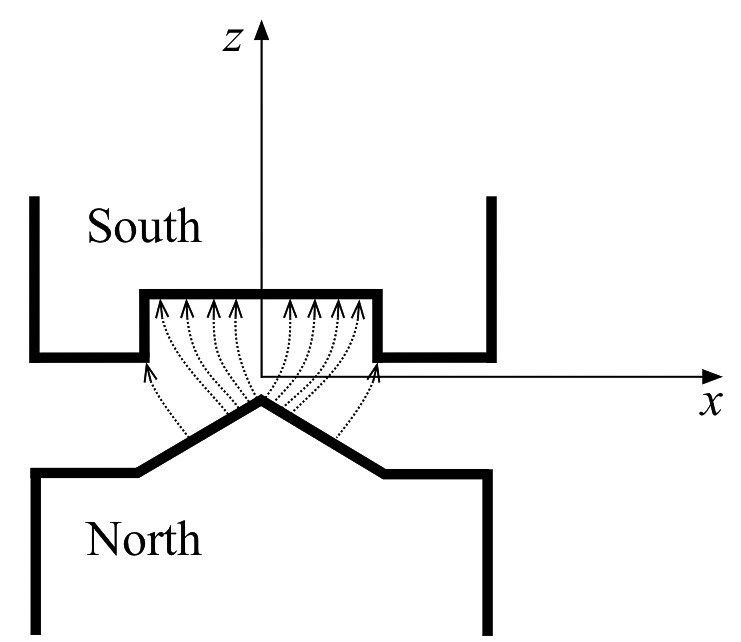
via Sneikder
- If $\myv S=+S\uv z$ which direction could the current loop move to lower it's energy?
- If $\myv S=-S\uv z$?
- If $\myv S=S\uv x (+0 \uv z)$?
These *directions* that a loop could move to lower its energy, correspond to the negative gradient of the potential $\myv B$ field, or in other words, the direction of a *force* acting on a current loop in such an inhomogenous magnetic field.
Measuring the magnetic moment of an electron
 One way to get a constantly circulating current running is to put a static charge on some insulator,
say a
cat, and set it spinning. Then the magnetic moment should be an integral over positions within the cat of charge density, $\rho(\myv r)$ times $dV$, then multiplied by $\myv v(\myv r)\times \myv r$. This should be a constant times the angular momentum of the cat.
One way to get a constantly circulating current running is to put a static charge on some insulator,
say a
cat, and set it spinning. Then the magnetic moment should be an integral over positions within the cat of charge density, $\rho(\myv r)$ times $dV$, then multiplied by $\myv v(\myv r)\times \myv r$. This should be a constant times the angular momentum of the cat.
Unlike a cat, there are some reasons to be skeptical that an electron can have any angular momentum at all (and therefore any magnetic moment...):
So, practically speaking...an electron might be a true *point* particle.
...But that just makes it more exciting for experimentalists to see if they can measure anything like a magnetic moment or find any other evidence that an electron might have angular momentum!
...And we have seen that the magnets producing an inhomogeneous field should push electrons with different magnetic-moment orientations in different directions (and with different magnitudes).
...and if the particles pass through the B-field fast enough, perhaps (inertia) they might not have enough time to re-orient in the field, so it's as if (*) they wouldn't have time to change their original orientation?
The Stern-Gerlach experiment
This is the idea behind the Stern-Gerlach apparatus. It's measuring $\mu_z$, the vertical (in the accompanying diagram) component the magnetic moment (which is proportional to the angular momentum), as long as the time the spin spends between the magnets is short compared to the time it takes for the spin to change orientations (more on that later).
As each silver atom passes thrugh the S-G magnet oriented as shown, it should deviate vertically by an amount proportional to the $z$ component of its unpaired electron's total angular momentum:
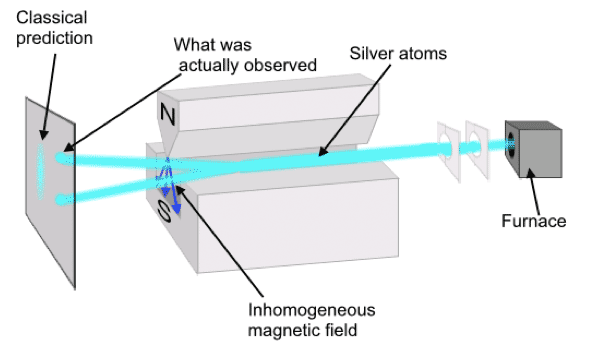
Classically, you'd expect a vertical smearing of the beam, due to at least two factors:
- Varying total angular momentum $S$, depending on how fast each electron is spinning and,
- Randomly varying orientations of $\myv S$ should lead to a continuous distribution of possible $S_z$ values. But...
Result of the Stern-Gerlach experiment: Carrying out the experiment, we observe that every last silver atom lands in one of two distinct patches on the screen!! !
Muddy points
Even in a constant magnetic field, there's a torque acting on a current loop, which should tend to align the angular moment, $S$ of a spinning body with the magnetic field. As the silver atoms move into the S-G magnet, won't that torque cause the spins to align with the magnetic field?
Based on our understanding of $U=-\myv \mu\cdot\myv B$, it is certainly true that the lowest energy state is when the current loop's $\myv \mu$ is aligned with $\myv B$.
However, angular momentum complicates this:
If the current loop arises from a spinning body that also has angular momentum $\myv S$, we saw in class that a torque acting on a spinning body will cause its angular momentum to precess around the direction of the external field, rather than simply "falling down" to its lowest energy state.
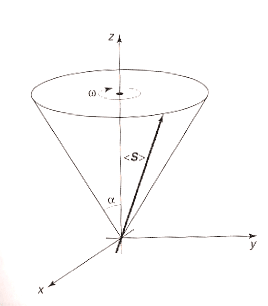
And for precession about the $z$ axis, , the $z$-component of the spin, $S_z$, remains constant. (Though both $S_y$ and $S_x$ are changing).
Here's a video demonstration of a spinning wheel responding to the torque of the gravitational field: (He's referring to torques acting on charged nuclear spins. But the same logic applies to charged electrons with spins.)
Conclusions
Conclusions that have eventually been drawn from the S-G experiment are that:
- Every electron ever measured has the same total angular momentum, $|\myv S|$.
- In a S-G apparatus oriented in the $z$ direction, the $z$ component of angular momentum has only ever been measured to be $$S_z=\pm \frac 12 \hbar.$$ We call these two states 'spin up' and 'spin down'.
See also: Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics (Physics Today, 2003).
Homework
Read
- The Prologue about Erwin's socks.
Lederhosen (literally 'leather pants') are a traditional kind of short pants in rural Germany (particularly Bavaria):
 Phineas Jones (Flickr)
Phineas Jones (Flickr)
- All of section 1.1 (and the rest of my notes--above)
- Section 1.2, through (up to and including) 1.2.2
Write up (and bring to class)
- Any questions that occurred to you in the readings.
- In chapter 1: Problems 7, 8, 9