
Probability and Quantum measurement [1.4]
 "Shooting dice", Michael Summers
"Shooting dice", Michael Summers
Probability: $Z$ analyzer
Can't say it any better than Figure 1.9:

For a S-G apparatus, $$\P_+=|\innerp{+}{\psi}|^2\nonumber$$ is the probability that a $Z$ analyzer receiving as input some wave function $\ket{\psi}$ will measure $S_z$ to have the value $+\hbar/2$.
And $\P_-=|\innerp{-}{\psi}|^2$ is the probability $S_z$ will be measured to have the value $-\hbar/2$.
If $\ket \psi=a\ket ++b\ket-$ then: $$\begineq \P_+ &=|\bra + \Big(a\ket + +b\ket-\Big)|^2\\ &= |a\innerp{+}{+}+b\innerp{-}{+}\\ &= |a|^2,\endeq$$ and similarly, $\P_-=|b|^2.$
So $\P_++\P_-=|a|^2+|b|^2$, and because $\ket \psi$ is normalized, the sum of the two probabilities is exactly 1.
Basis vectors and coordinate systems
I've previously defined the column vector representations of $\ket +$ and $\ket -$ as $$ \ \ \ket + \equiv \begincv 1\\ 0 \endcv; \ \ \ket - \equiv \begincv 0 \\ 1 \endcv, $$ Together with the definition of the inner (dot) product definition of a bra-ket, you can readily see that kets are both normalized to 1: $$\innerp{+}{+}=\begincv 1 & 0\endcv\begincv 1\\ 0 \endcv=1,$$ $$\text{and }\ \ \ \innerp{-}{-}= 1.$$ They are also mutually orthogonal: $$\innerp{+}{-}=\begincv 1 & 0\endcv\begincv 0\\ 1 \endcv=1\cdot0+0\cdot1=0,$$ $$\text{and }\ \ \ \innerp{-}{+}= 0.$$ We initially postulated that any state vector can be represented as the superposition (completeness) $$\ket \psi = a\ket + + b\ket -.$$ (We can also say these two vectors span the space of all possible states.) Therefore...
The set $\{\ket +, \ket -\}$ forms an orthonormal basis set for the $Z$ analyzer.
The unit vectors for a Cartesian coordinate system are all normalized to have unit length: $$\uv i \cdot \uv i=1$$ $$\uv j \cdot \uv j=\begincv 0 & 1\endcv \begincv 0\\1\endcv = 0^2+1^2=1$$ They are all mutually perpendicular, or orthogonal $$\uv i \cdot \uv j=\begincv 1 & 0\endcv \begincv 0\\1\endcv = 1\times 0+0\times 1=0$$ We have also seen that they are complete: Any vector in 2-dimensions can be written as a linear combination of the 2 basis vectors $$\myv V=V_x\uv i+V_y\uv j.$$ These three characterics of the set $\{\uv i, \uv j\}$ are what define an orthonormal coordinate system.
By the way, the unit vectors of polar coordinates, $\{\uv r, \uv \theta\}$ also fulfill these conditions, even though the directions of the unit vectors change depending on position.
Projection
The inner product of one of the basis bras with a state vector returns the coefficient of the corresponding ket: $$\begineq \innerp{+}{\psi}&=\bra + ( a\ket + + b\ket -)\\ &= a\innerp{+}{+}+b\innerp{+}{-}\\ &=a\cdot 1+b\cdot 0 = a.\endeq$$
The component, $V_x$, of the vector $\myv V$ along the $x$ axis is given by $$\begineq V_x &= \uv i\cdot \myv V=\uv i \cdot (V_x\uv i+V_y\uv j)\\ &=V_x\uv i\cdot\uv i+V_y\uv i\cdot\uv j\\ &= V_x\cdot 1+V_y\cdot 0 = V_x\endeq$$ Or, $V_x$ is the projection of $\myv V$ in the $x$ direction.
Coordinate transformations
A state vector can be written as a superposition of the basis vectors of the $Z$ analyzer, say $\ket \psi = a\ket + +b\ket -$.
But an $X$ analyzer has a different set of basis vectors. And in this basis, the same state vector has a different representation $$\ket \psi = a' \ket+_{\color{red}_x}+b'\ket-_{\color{red} -}.$$
A change of coordinate systems does not change a vector. But the vector's components in the new coordinate system will be different.
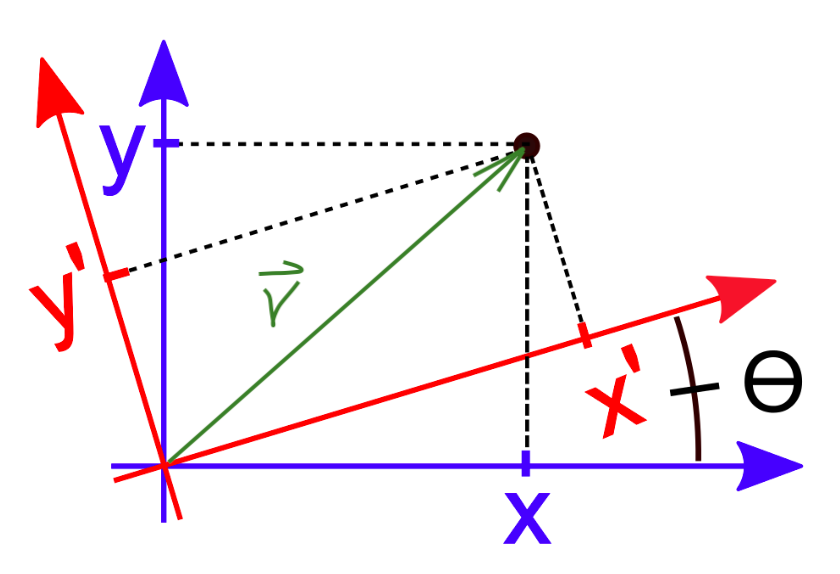
In the new coordinate system, the vector is written as:
$$\myv V=a'\,\uv i'+b'\,\uv j',$$
where $a'=\myv V\cdot \uv i'$ and $b'=\myv V\cdot \uv j'$.
How do we know that the $X$ analyzer has a different set of basis vectors? Because of these two:
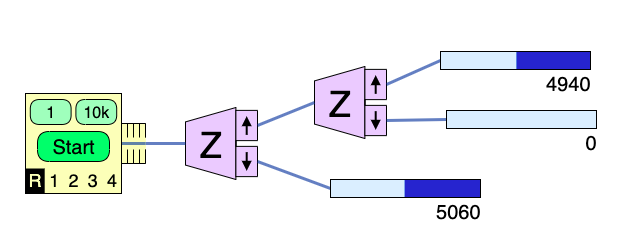
The probability of the top-right channel is $P\uparrow=|\innerp{+}{+}|^2=1$. But...
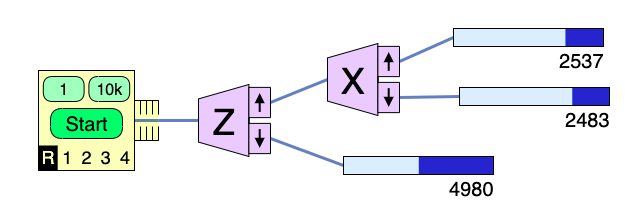
Here the probability of the top-right channel is $\P_{\uparrow x}=|\innerp{+}{+}_x|^2$, which is considerably less than 1. So $\ket +_x$ is not the same as $\ket +$.
Now, $\ket +_x$, like any quantum state vector, could be written as a superposition of the $Z$ basis states:
$$\ket +_x=a\ket++b\ket-.$$
Without proof (though read McIntyre to see his reasoning...)
The basis vectors for the $X$ analyzer, in terms of the $Z$ basis states are: $$\ket +_x = \frac 1{\sqrt 2}\Big( \ket + +\ket -\Big)\equiv \frac 1{\sqrt 2}\begincv 1\\1\endcv$$ and $$\ket -_x = \frac 1{\sqrt 2}\Big( \ket + - \ket -\Big)\equiv \frac 1{\sqrt 2}\begincv 1\\-1\endcv$$
With these definitions, that probability for the top right channel of the second experiment is: $$\begineq \P_{\uparrow x}&=|\innerp{+}{+}_x|^2 =\left|\begincv 1 & 0\endcv\frac{1}{\sqrt 2}\begincv 1 \\1\endcv\right|^2\\ &=\left|\frac{1}{\sqrt 2}\cdot 1\right|^2 =\frac 12. \endeq$$
And here are the basis vectors for the $Y$ analyzer.
The basis vectors for the $Y$ analyzer, in terms of the $Z$ basis states are: $$\ket +_y = \frac 1{\sqrt 2}\Big( \ket + +i\ket -\Big)\equiv \frac 1{\sqrt 2}\begincv 1\\i\endcv$$ and $$\ket -_y = \frac 1{\sqrt 2}\Big( \ket + - i\ket -\Big)\equiv \frac 1{\sqrt 2}\begincv 1\\-i\endcv$$
Muddy points
Problem 5 asks you to consider a beam of particles "which has been prepared" in the state $$\ket\psi = \frac 2{\sqrt{13}}\ket + +i\frac 3{\sqrt{13}}\ket -.$$ Drew asked:
How do you prepare a beam in such a [ridiculously arbitrary] superposition state?
Well, A $Z$ analyzer consists of an S-G magnet with its South pole facing up in the $+z$ direction. We can make an $X$ analyzer by taking the same S-G magnet and turning the South pole by $90^o$ so that it faces in the $+x$ direction.
We have not considered how to describe the state of the outgoing beam if we rotated the South pole by only $45^o$ from $z$ towards $x$. Perhaps the spin up state of such an analyzer might be a coherent superposition of $\ket +$ and $\ket +^x$...like this? ($C$ is a normalization constant, that we'll figure out later...) $$\begineq \ket +_{45^o} &\stackrel {?}{=} C\big(\ket + + \ket +_x\big)\\ &=C\big(\begincv 1 \\0\endcv +\frac{1}{\sqrt 2}\begincv 1 \\1\endcv\big)\\ &=C\big(\begincv 1+\frac 1{\sqrt 2} \\ \frac 1{\sqrt 2}\endcv\big).\\ \endeq$$
It looks like we have quite a bit of freedom to rotate a single S-G magnet in both the $x-z$ and $y-z$ and $x-y$ planes, and this might be enough to get any arbitrary "prepared" state...
Homework (1.4)
In Chapter 1, do problems (but you don't need to do the histograms) 5,6,10,11
Read section 1.2.3 on Superposition of States (and how they differ from mixed states). Come up with a question about this material.
On the Spins simulator... select each of the unknown (but coherent) outputs 1, 2, and 3 (harder!) and use different analyzers (with counters) to see if you can figure out what the initial state was.