The story so far...

We're using separation of variables, trying to find solutions to the time-independent Sch equation when $V=V(x)$, which can be written like: $$\Psi(x,t)=\varphi(x)T(t)=\varphi(x)e^{-iEt/\hbar}$$ where $E$ is the constant in the time-independent Schrödinger: $\varphi(x)$ is a solution of the time-independent Schrödinger equation: $$-\frac{\hbar^2}{2m}\frac{\del^2\varphi}{\del x^2} + V(x)\varphi = E\varphi(x).$$ We're finally at the point of putting in a particular potential, $V(x)$ to see if we can find a solution...

Infinite sqare well

Model an infinite well as: $$V(x) = \left\{ \begin{array}{c} \infty & x < 0\\ 0 & 0 < x < a \\ \infty & a < x \end{array} \right.$$ In my notes, the finite portion of the well is between $0 < x < a$.
McIntyre uses $0 < x < {\color{red}L}$.

This can be generalized to 3 dimensions: Then we'll call it the particle in a box problem.

The probability of finding the particle outside of the well is 0, so already we can write $$\varphi(x)=0 \ \ \ \text{ outside of }\ 0 \lt x \lt a.$$

The time independent Schrödinger equation is $$-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\varphi(x) + V(x)\varphi(x) = E\varphi(x).\label{curvature}$$ So inside the well, we must solve: $$-\frac{\hbar^2}{2m}\frac{\partial^2\varphi(x)}{\partial x^2} = E\varphi(x).$$ or $$ \frac{\partial^2\varphi(x)}{\partial x^2} = -k^2 \varphi(x).$$ where $k=\frac{\sqrt{2mE}}{\hbar}$ is a positive real number. (You'll show that $E>0$ in problem 2.2.)

A general solution to this differential equation can be written: $$A\sin kx+B\cos kx.$$

Some characteristics of the wave function (to be demonstrated with more rigor later):

$\varphi(x)$ is *always* continuous,
$\varphi'(x)$ is continuous where $V'(x)$ is continuous. (Not at the edge of the infinite well!)

The solution(s) need to be continuous with the solution outside the well, so $\varphi(0)=\varphi(a)=0$, and this will narrow the allowed solutions to $$\varphi(x) = A\sin k x.$$

We want $\varphi(a)=0$ which implies $ka=\pm n\pi$, so the solutions occur for values $$k_n=\frac{n\pi}{a}\ \ \ \text{where}\ n=1, 2, 3,....$$

Problem: Why not $n=0$? Why don't $n=-1$ or $n=-2$ show up in the list of allowed $n$ values?

The relationship between $k$ and $E$ tells us that solutions do not exist for just any ol' E, but only for certain values of that separation constant...

Allowed $E$'s: $$E_n=\frac{\hbar^2k_n^2}{2m}=\frac{n^2\hbar^2\pi^2}{2ma^2}=\frac{n^2h^2}{8ma^2}.$$

Problem: Write down the integral you need to do to normalize $\varphi_n(x)$

The normalized solutions (eigenfunctions) of the stationary Schrödinger equation for a particle of mass $m$ in the infinite, 1-d square well with $V(x)=0$ for $0 < x < a$ are: $$\varphi_n(x) = \sqrt{\frac{2}{a}}\sin\left( \frac{n\pi x}{a}\right)\equiv \ket{n}$$

For example, the first three states ($x$ plotted in units of $a$ and $y$ plotted in units of $\sqrt{2/a}$:

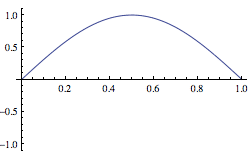$\ket 1$, the ground state

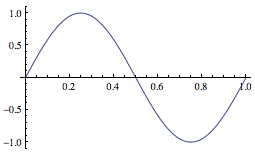$\ket 2$, first excited state

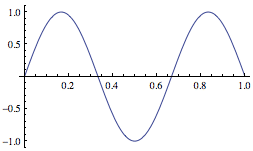$\ket 3$

Some characteristics of the solutions...

Equation (\ref{curvature}) can be interpreted to say something about the curvature of the wave function:$$\frac{\partial^2\varphi(x)}{\partial x^2} \propto (E-V)\varphi(x).$$
The number of nodes is increasing with $n$.
W.r.t. the center of the well, solutions are alternately symmetric and anti-symmetric.
Problem Sketch $\ket 5=\varphi_5(x)$.

Stationary states

The simplest general solution consists of just one eigenfunction $\varphi_n(x)$ multiplied by its time dependence $T(t)=e^{-iEt/\hbar}$: $$\varphi_n(x,t)=\varphi_n(x)e^{-iE_nt/\hbar}.$$

Calculate the expectation value for position: $$\begineq \langle x \rangle =\bra{\varphi_n}\hat x\ket{\varphi_n} =& \int_0^a\varphi_n^* x \varphi_n \,dx\\ =& \int_0^a \varphi^*_n(x)x\varphi_n(x)e^{-i(E_n-E_n)t/\hbar}\,dx\\ =& \int_0^a \varphi_n(x)x\varphi_n(x) \,dx. \endeq $$

$\langle x \rangle$ is not time dependent, and in general, $\langle f(x) \rangle$ is time independent as well for such a stationary state.

For example, in the $\varphi_2$ state, $$\begineq \bra{\varphi_2}\hat x\ket{\varphi_2} &= \int_0^a \sqrt{\frac{2}{a}}\sin\left(\frac{2 \pi x}{a}\right) x \sqrt{\frac{2}{a}}\sin\left(\frac{2 \pi x}{a}\right)\,dx \\ &= \frac{2}{a}\int_0^a x \sin^2\left(\frac{2 \pi x}{a}\right) \,dx = \frac{a}{2}.\endeq$$ [Using WA.]
Oh, $x=a/2$ is the middle of the well!

Problem: Sketch the probability density for $\ket 2$. What is the probability density for finding the particle at the middle of the well?

Calculate the expectation value of the Hamiltonian: $$\begineq \langle H \rangle =& \int_0^a\varphi_n^* \frac{1}{2m}\left(\frac{h}{i}\frac{\del}{\del x}\right)^2 \varphi_n \,dx\\ =& -\frac{\hbar^2}{2m} \int_0^a \varphi^*_n(x)\frac{\del^2\varphi_n(x)}{\del x^2}e^{-i(E_n-E_n)t/\hbar}\,dx\\ =& -\frac{\hbar^2}{2m}\int_0^a \varphi_n(x)(-k_n^2)\varphi_n(x) \,dx \\&=\frac{\hbar^2k_n^2}{2m} = E_n. \endeq $$

$\langle H \rangle$ is also time-independent and is equal to the separation constant, $E_n$, for the state $\varphi_n$.

Classically, $H$ corresponds to the sum of kinetic and potential energy, which we just call the total energy, so at this point we can start talking about $E$ as 'energy' and not just as 'the separation constant'.

But the most general solution is a normalized linear combination, or superposition of the $\varphi_n$ functions: $$\begineq\varphi(x,t)=&\sum_n c_n \varphi_n = \sum_n c_n \varphi_ne^{-iE_nt/\hbar}\\ =& c_1\sqrt{2/a}\sin(\pi x/a)e^{-ih\pi t/(4ma^2)} \\ &\ \ \ +c_2\sqrt{2/a}\sin(2 \pi x/a)e^{-i4h\pi t/(4ma^2)} \\ &\ \ \ +c_3\sqrt{2/a}\sin(3 \pi x/a)e^{-i9h\pi t/(4ma^2)} + ...\endeq$$