
Sketching solutions to the Schrödinger equation
It's possible to sketch solutions to the time-independent Sch equation by thinking about what it implies for the curvature of $\varphi(x)$.
We'll apply this to find:
- Infinite well: How the energy changes if the well narrows.
- Finite well: How do the energy changes compared to the infinite well case...
- Asymmetric wells.
- 1-d harmonic oscillator potential
Curvature
The time-independent Schrödinger equation can be written as $$\frac{\del^2 \varphi(x)}{\del x^2}=\frac{2m(V(x)-E)}{\hbar^2}\varphi(x).$$ On the left is 2nd derivative of $\varphi$: the rate of change of the slope which is the curvature (concavity) of $\varphi(x)$.
In the infinite well, there are solutions when $E \gt V(x)$
When $\varphi(x) \gt 0$ is the curvature positive or negative?
When $\varphi(x) \lt 0$ is the curvature positive or negative?
In both cases this causes the function to curve (a) away from the $x$-axis, (b) back towards the $x$-axis ?
Here are the first three solutions for the infinite well. Do your answers agree with these solutions?
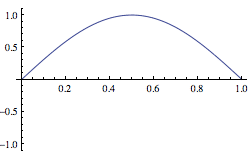 $\ket 1$, the ground state |
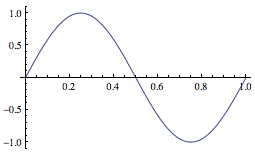 $\ket 2$, first excited state |
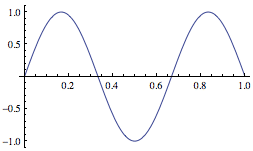 $\ket 3$ |
The tendency above means that $\varphi(x)$ will not "blow up", but rather oscillate back and forth around the $x$-axis.
Curvature and energy
That Sch equation once again: $$\frac{\del^2 \varphi(x)}{\del x^2}=\frac{2m(V(x)-E)}{\hbar^2}\varphi(x):$$
What happens to the curvature if you increase $E$ (while still assuming that $E\gt V(x)$)?
What will this do to the frequency of oscillations of $\varphi(x)$?
Again, check your answers against our infinite well solutions.
And now you are in a position to answer some even more interesting questions:
- Consider an infinite square well of width $a=2$, that is, $V(x)=0$ for $0\lt x\lt 2$, and $V(x)=\infty$ outside of that region. Sketch $\varphi_3(x)$ which has 2 nodes: between 0 and 2 it crosses the $x$-axis 2 times.
- Now, consider a narrower infinite square well of width $a=1$. Sketch $\varphi_3(x)$ (with 2 nodes) for this narrower well.
- For which well is the curvature of the wave function greater at the middle of the well?
- Consult our expression above for the second derivative. Does the wave function with greater curvature likely have a higher energy or a lower energy? (You should check your answer against the expression for the energy of $\varphi_n(x)$, as it depends on $a$.)
Compare this with the expression we derived for the energy of the stationary states... $$ E_n=\frac{n^2h^2}{8ma^2} $$
Using what you now know about the oscillations, sketch $|5\rangle$ (4 nodes) for the asymmetric infinite well.
Finite well
Now consider a finite well: $$V(x)=\left\{ \begin{array}{c} V_0 & x \lt 0 \\ 0 & 0 \lt x \lt a \\ V_0 & x \gt a \end{array} \right. $$
In the "wall region" (outside the well) when $E\lt V_0$, $\varphi(x)$ must curve away from the $x$-axis. But since the curvature is also proportional to $\varphi$, a normalizable solution such that $\varphi(x)\to 0$ as $x\to\pm\infty$ might barely be possible for just the right conditions.
In fact there are two linearly independent possible solutions. Adding them for a general solution. $$\varphi(x)=Ae^{+\alpha x}+B^{-\alpha x},$$ where $\alpha = \sqrt{2m(V_0-E)/\hbar^2}$.
Oh one more thing. Unless $V(x)$ is infinite outside the well, then it's also the case that the slope (derivative) $\varphi'(x)$ is continuous at on either side of the well walls at $x=0$ and $x=a$.
Sketching ...
- Now consider a finite well of width $a=1$. You're going to compare this with the infinite well of width $a=1$ Under these conditions as we saw in class, the wave function is not zero outside the well, but it is dieing off as $x\to\pm\infty$. Sketch your best guess of $\varphi_3(x)$ (with two nodes) for this case!
- How does the curvature at the middle of the well compare in the case of the infinite well, and in the finite well? And deduce from this which of these two wells has a $\varphi_3$ solution with a greater energy...
Writing Schrödinger's equation in the form... $$\frac{\del^2 \varphi(x)}{\del x^2}=\frac{2m(V(x)-E)}{\hbar^2}\varphi(x),$$ relates the curvature of the wave function $\varphi(x)$ to the product of the wave function itself, and the quantity $V(x)-E$. A summary of our deliberations:
Wherever $\color{blue}E \gt V(x)$, the wave function is curving back towards the $x$ axis.
Wherever $\color{blue}E \lt V(x)$ , the wave function is curving away from the $x$ axis.
As $\color{blue}|E - V(x)|$ grows larger, the magnitude of the curvature of the wave function increases.