Phase vs Group velocity
What about our situation that $2 v_\text{quantum} = v_\text{particle}$?
It is frequently the case that the phase velocity of wave peaks is not necessarily the same as the group velocity of the shape or envelope of a wave pulse.
But how could we pick out the two kinds of velocity??
Our wave function $$\begineq\Psi(x,t)&=\frac 1{\sqrt{2\pi}}\int_{-\infty}^{+\infty}\phi(k)e^{i\left(kx-\frac{\hbar k^2}{2m} t\right)}\,dk\\ &=\frac 1{\sqrt{2\pi}}\int_{-\infty}^{+\infty}\phi(k)e^{i\left(kx-\omega t\right)}\,dk,\\ \endeq$$ where in the QM case $$\omega=\frac{\hbar k^2}{2m}.$$ In general the formula $\omega(k)$ is called a dispersion relation and is different for different kinds of waves.
What we called the quantum speed $$v_\text{quantum}=\frac{\omega}{k}=\frac{\hbar |k|}{2m}$$ is the phase velocity: the speed of wave crests (or valleys).
How to calculate the "envelope" speed?
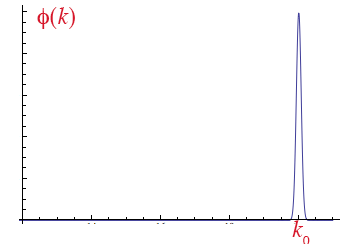Consider a wave pulse that has a distribution $\phi(k)$ which is narrow, and peaked near a value $k_0$.
The picture at right is *not* a picture of the wave function, (a function of $x$). Actually, if $\phi(k)$ is narrowly peaked in $k$, we know that $\Psi(x,0)$ must be a function which is broad in $x$ to satisfy the uncertainty principle.
Making a Taylor (series) expansion of $\omega(k)$ about the value $k_0$: $$\omega(k)=\omega(k_0)+\omega'(k_0)[k-k_0]+... \equiv \omega_0+\omega_0'[k-k_0]+...$$ where $\omega_0'(k_0)\equiv \left. \frac d{dk}\omega(k)\right|^{k=k_0}$.
So the wave function could be approximated as $$\begineq \Psi(x,t) &=\frac 1{\sqrt{2\pi}}\int_{-\infty}^{+\infty}\phi(k)e^{i\left(kx-\omega t\right)}\,dk,\\ &\approx\frac 1{\sqrt{2\pi}}\int_{-\infty}^{+\infty}\phi(k)e^{i\left(kx-[\omega_0+\omega_0'(k-k_0)] t\right)}\,dk,\\ &=\frac 1{\sqrt{2\pi}}e^{i(\omega_0-k_0\omega_0')t} \int_{-\infty}^{+\infty}\phi(k)e^{i(kx-\omega_0'kt)}\,dk,\\ &=\frac 1{\sqrt{2\pi}}e^{i(\omega_0-k_0\omega_0')t} \int_{-\infty}^{+\infty}\phi(k)e^{ik\left(x-\omega_0' t\right)}\,dk,\\ &\equiv A(t)f(x-\omega_0't), \endeq $$ where $f(x-\omega_0't)=\int[...]\,dk$, and $A(t)$ comprises all the factors in front of the integral.
It can readily be seen that $A^*(t)A(t)=\frac{1}{2 \pi}=$constant.
So, the probability density: $$\Psi(x,t)^*\Psi(x,t)=\frac 1{2\pi}f^*(x-\omega_0't)f(x-\omega_0't)$$ is a function of $(x-\omega_0't)$. It is just a shift of the function $\Psi(x,0)^*\Psi(x,0)$ moving with the speed $\omega_0'$.
This is apparently the group velocity. $$\begineq \omega_0'&\equiv \left.\frac{d}{dk}\omega(k)\right|^{k_0} =\left.\frac{d}{dk}\frac{\hbar k^2}{2m}\right|^{k_0} \\ &= \frac{\hbar k_0}{m} =v_\text{particle}=2v_\text{quantum}. \endeq $$
Returning to that animation that we started with...
Which is faster, the group or phase velocity?
But we have the case where group velocity is faster than the phase velocity.
All kinds of relationships are possible between the group and phase velocity, including one of them moving in the opposite direction from the other!
In general
$$v_\text{phase}=\frac \omega k$$ $$v_\text{group}=\frac{d\omega}{dk}$$
For electromagnetic waves (which are actually QM waves) the group velocity in vacuum is $c$, and determines the speed of photons. The phase velocity can exceed $c$.
