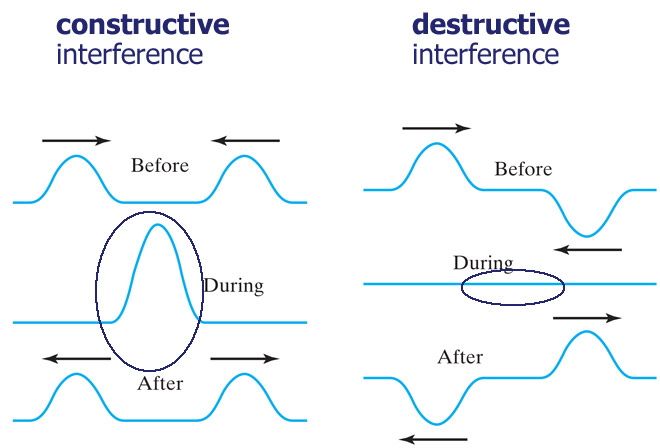
Interference

Using the principle of superposition, you can probably guess what happens when two equal, or equal-and-opposite pulses, travelling towards each other meet:

Waves on the surface of water in 2-d

Wave pulses on the surface of a tank of water exhibit constructive and destructive interference.

Dipping 2 fingers repeatedly into a tank of water (in the picture, on the left side, at the centers of the 2 circles) yields this sort of pattern of "interference".

Where two crests meet, the height of the wave should be twice as high as one. Where two troughs meet, twice as low.

Where a trough and crest meet, total cancellation.

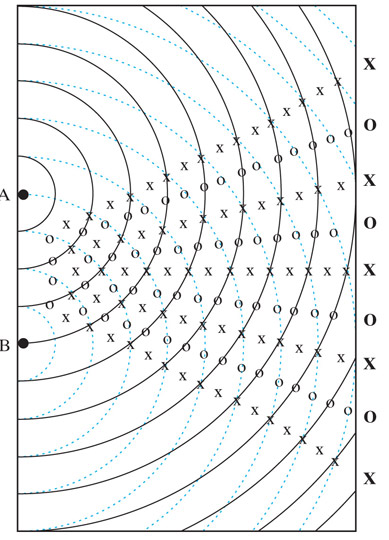
In the accompanying diagram:

  • The brightest spots indicate constructive interference: where two crests meet (one from each source), and the wave height is 2 X the height of one crest.
  • The darkest spots also indicate constructure interference: where two troughs meet (one from each source). and the wave height is 2 X the depth of one trough.
  • The in-between-gray-blue spots indicate destructive interference: where a crest from one source meets a trough from the other source, cancelling each other out.

The "nodes" or locuses of destructive interference, appear to form lines which roughly radiate away from a point between the two sources.

 

Interference patterns

We can pictorially calculate how this pattern should come out by marking up a diagram of the wave pattern from the two sources with
  • "X" at places where crests meet crests (or troughs meet troughs), and
  • "O" at places where a crest from one meets a trough from the other.
An observer standing at the right side of the pool would see large waves rolling in at points marked with an X (lots of energy), and no wave motion at points marked O (no wave energy).

Young's double-slit

Have the waves from just one source hit a screen with two openings in it. Each opening acts like a "source" in its own right. But now the two "sources" are always in synch with each other, and are guaranteed to have the same frequency (that of the original plane wave coming at the wall).

Exercises with ripple tanks

You'll use Paul Falstad's ripple tank simulator to explore interference patterns.

Two sources (like two slits)

  1. Choose "Example: Two Sources", set the Source Frequency to the middle of the range.
  2. Now, drag the two sources up to the top of the picture frame

You'll see an interference pattern, with blurry "nodes" between the areas of constructive interference.

Vary the following parameter, and in each case describe how the spacing of the nodes changes (at the bottom of the screen) as you:

  1. Increase the distance, $a$, between the two sources.
  2. Decrease the frequency of the waves--this should *increase* the wavelength, $\lambda$ of the waves.
  3. Now, imagine a line a distance $d$ away from the two sources. What happens as you increase $d$ (that is, move your line down towards the bottom of the screen)?

$$\lambda=2d\sin\Delta\theta$$

Single slit

  1. Choose "Example: plane wave", set the Source Frequency to the middle of the range.
  2. Now, Right click with your mouse on the picture to "Add Wall". You'll eventually add a second wall. Move, and drag the ends of the little walls you get to arrange to have just a single slit in a wall which is about a third of the way down the screen.

You'll see a less distinct interference pattern, with blurry "nodes" on either side of an area of constructive interference.

Vary the following parameters, and in each case describe how the spacing of the nodes changes (at the bottom of the screen) as you:

  1. Increase the width of the slit, $w$.
  2. Decrease the frequency of the waves--this should *increase* the wavelength, $\lambda$ of the waves.
  3. Now, imagine a line a distance $d$ away from the two sources. What happens as you increase $d$ (that is, move your line down towards the bottom of the screen)?

Two slit interference pattern

We have seen that you can qualitatively find the interference pattern from 2 slits by drawing the peaks and troughs from each slit, and then seeing where there is constructive or destructive interference.

The criteria for constructive interference at any point is that crests from both sources must arrive at the same time. We could measure the distance to slit 1 (call it $d_1$) and the distance to slit 2 (call it $d_2$).

The criteria for constructive interference is that the path difference ("$\color{blue}{\delta}$" in the diagram) be an integer number of wavelengths: $$\delta = n \lambda.$$ where $n$ is an integer, one of 0, 1, 2, 3, ...

Working this out for the case that the slits are much closer to each other than the distance to a "screen" on which we're observing the diffraction:

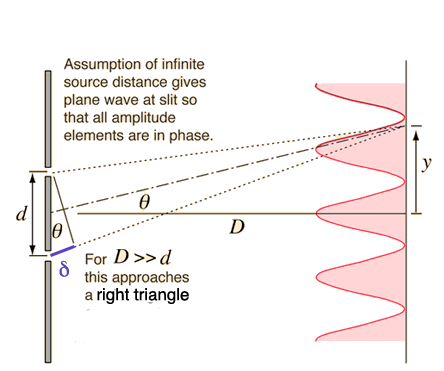
As long as $D \gg d$, the triangle close to the slits is a right triangle with $\sin \theta=\delta/d$. Putting this together with the previous condition on the path difference, the condition for a maximum at the screen is: $$\sin\theta=\frac{n\lambda}{d}$$ Since $y/D\approx\sin\theta$, the distance on the screen between neighboring peaks of the diffraction pattern on the screen is approximately $$\Delta y = \lambda\frac{D}{d}.$$

Image credits

Hyperphysics