Linear algebra

Linear algebra deals with vector spaces. Functions or transformations that map one vector into another can be represented by matrices. Usually we think of vector spaces as having a finite number of dimensions (often 3), but the theory also finds applications in infinite-dimensional spaces, such as the set of periodic functions on a bounded interval.

Matrix Multiplication

Consider two vectors, described in terms of their Cartesian components as $\myv a=(1,1,0)$ and $\myv b=(-1,2,3)$. Their dot product is $$\myv a\cdot\myv b=a_xb_x+a_yb_y+a_zb_z=1*-1+1*2+3*0 = 1.$$ We can represent the first vector as a "row vector", $$\myv a=\begincv 1 & 1 &0\endcv$$ and the second one as a "column vector": $$\myv b=\begincv -1 \\ 2 \\ 3 \endcv$$. The dot product can be laid out as a multiplication of a "row" and a "column"... $$ \myv a \cdot \myv b=\begincv 1 & 1 &0\endcv\begincv -1 \\ 2 \\ 3 \endcv= (1)(-1)+(1)(2)+(0)(3)=1$$ using a convention for multiplying rows by columns that you'll add the product of

Or, using summation notation $\myv a\cdot\myv b=\sum_i a_ib_i$.

Probably you can see how to extend this to vectors with more (or fewer) dimensions than 3!

It's probably clear that $a_2$ is the 2nd element of $\myv a$.

We can extend this row-column multiplation to matrices. Consider a $3\times 3$ matrix: $$\mym A=\begincv 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9\endcv $$ We can (eventually) use the summation notation to describe, compactly the way to multiply two such matrices, but first we need a convention to indicate, with subscripts like we did for vectors, individual elements of the matrix. We'll say that

$A_{ij}$ means the number in row $i$ and column $j$ of the matrix $\mym A$.

With this definition $$\mym A=\begincv A_{11} & A_{12} & A_{13}\\ A_{21} & A_{22} & A_{23}\\ A_{31} & A_{32} & A_{33}\endcv $$ And comparing these definitions with the value specified for $\mym A$ above, we can see that $A_{11}=1$, $A_{12}=2$, $A_{32}=8$, $A_{23}=6$, and $A_{33}=9$, among others.

Now we can use row-column multiplication to define the inner product of two matrices:

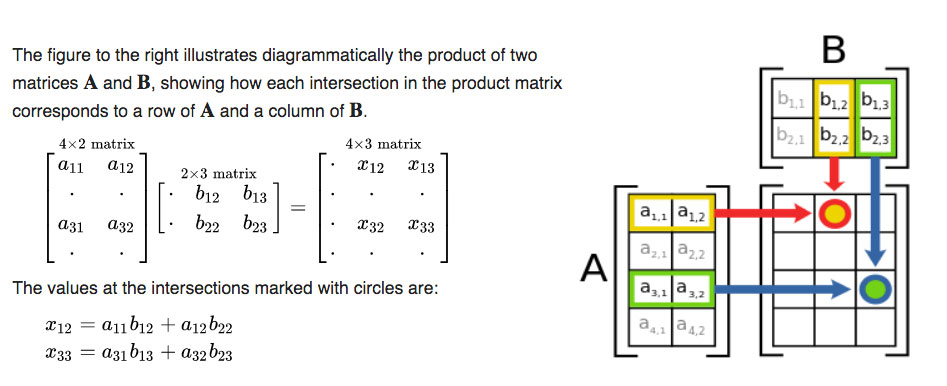
Matrix Multiplication [Wikipedia]

Using summations, we can express the elements of matrix $\mym x$ as: $$x_{ik}=\sum_ja_{ij}b_{jk}.$$

As you can probably see, we can only multiply an $m\times n$ matrix by a $j\times k$ matrix using row-column multiplication if $n=j$.

After a while, it becomes tiresome to write out all these sums, so now many authors use the "Einstein summation convention":

The Einstein summation convention: If you see an expression involving the products of matrix elements (without the $\sum$ symbol), you should know to nevertheless sum over any of the indices which are repeated.

The dot product of two vectors can be written with this convention as: $$\myv{a}\cdot\myv{b}=\sum_i^3a_ib_i \equiv a_ib_i.$$

Multiplying one matrix by another... $$\mym M \mym N=\sum_j M_{ij}N_{jk} \equiv M_{ij}N_{jk}.$$

The cross product of two vectors can be written in the following equivalent ways...

$$\begineq \myv{a}\times\myv{b} &=& \det\begincv\uv{e}_1&\uv{e}_2&\uv{e}_3 \\ a_1&a_2&a_3\\ b_1&b_2&b_3\endcv\\ &=&\sum_{i}\sum_{j}\sum_{k}\varepsilon_{ijk} \uv{e}_iA_j B_k \equiv \varepsilon_{ijk}\uv e_ia_j b_k .\endeq$$

using the Levi-Cevita symbol $\varepsilon_{ijk}$ which is a rank-3 tensor (a $3\times 3\times 3$ matrix!) defined as:

$$\varepsilon_{ijk}=\left\{\begin{array}{} 0 & {\rm if\ not}(i\neq j\neq k)\\ 1 & {\rm even\ permutations\ of\ } 123\\ -1 & {\rm odd\ permutations\ of\ } 123 \end{array}\right. $$

Simultaneous equations

We'd like to solve a set of simultaneous equations, such as:
$x+2y+3z = 1$
$3x+3y+4z = 1$
$2x+3y+3z = 2$

These can be written in matrix form as $\mym A\myv r=\myv c$, where $\mym A$ is a matrix and $\myv r$ and $\myv c$ are column vectors: $$ \left( \begin{array}{c} 1 & 2 & 3\\ 3 & 3 & 4\\ 2 & 3 & 3 \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \end{array} \right) = \left( \begin{array}{c} 1 \\ 1 \\ 2 \end{array} \right) $$

There is a unique solution, it turns out, if the determinant of the matrix is not 0. Calculate it: $\det\mym A=4$.

Schematically, the way to solve this is to find (more about that later) $\mym A^{-1}$, the inverse of $\mym A$. If we had that, we could multiply both sides of the equation by $\mym A^{-1}$ to find... $$\begineq \mym A^{-1}\mym A\myv r &=&\mym A^{-1}\myv c\\ \myv r&=&\mym A^{-1}\myv c. \endeq$$

Using Octave, we find that $$\mym A^{-1}=\frac{1}{4}\begincv -3 & 3 & -1\\ -1 & -3 & 5\\ 3 & 1 & -3\endcv ,$$ and $\mym A^{-1}\,\mym A$ is $$\mym A^{-1}\,\mym A = \begincv 1 & 0 & 0\\ 0& 1 & 0\\ 0 & 0 & 1\endcv $$. This is the "identity matrix", $\mym 1$. Multiplying this by $\myv r$: $$\mym 1 \myv r = \myv r.$$ So, the solution to this set of equations is: $$\begineq \myv r&=&\mym A^{-1}\myv c\\ \left( \begin{array}{c} x \\ y \\ z \end{array} \right) &=& \frac{1}{4}\begincv -3 & 3 & -1\\ -1 & -3 & 5\\ 3 & 1 & -3\endcv \left( \begin{array}{c} 1 \\ 1 \\ 2 \end{array} \right) =\begincv -\frac 12 \\ \frac 32 \\ -\frac 12 \endcv \endeq$$

Tensor?

In order of increasing complexity...

		tensor rank
number	number of marbles in a bag	N/A
distance scalar	5 miles	0
position vector	1.5 mi north, 2.2 mi east, 3 stories up	1
moment of inertia matrix		2

Be aware that there will be some switching back and forth between writing the Cartesian components of a vector $\myv{r}$ as (equivalentl):

$$\myv{r}=x\uv{x}+y\uv{y}+z\uv{z} \equiv r_1\uv{e}_1+r_2\uv{e}_2+r_3\uv{e}_3.$$