Taylor series / Taylor expansion
The question is....
- If we have a function $f(x)$,
- and we know lots of things about the function when $x=a$, such as
- the value of the function at $x=a$, that is $f(a)$,
- derivatives w.r.t. $x$ at $x=a$, that is $f'(a), f''(a), f'''(a),$ etc.
- Evaluating this at $x=a$ to find $c_0=f(a)$.
- Take the first derivative, and evaluate at $x=a$ to find that $c_1=f'(a)$.
- Take another derivative, and evaluate at $x=a$ to find $2c_2=f''(a)$.
- Google around a bit to find out....What's a Maclaurin series--how is it related to a Taylor series?
- If you Taylor expand $f(x)=\ln(x)$ around $x=1$, the Taylor series is a good approximation only for a limited range of $x$. Use some math package to make a graph with
- $f(x)=\ln(x)$,
- 5 terms in the Taylor expansion,
- 12 terms in the Taylor expansion.
- Derive the Madhava sequence for $f(x)=\cos(x)$: a Taylor expansion about $x=0$.
- Derive the Taylor expansion for $f(x)=e^{kx}$ (where $k$ is a constant) about $x=0$.
- Use the two results above, and the Madhava sequence for $\sin(x)$ to prove Euler's equation: $e^{ix} = \sin x +i\cos x$.
- The tangent of a $45^o$ angle is $\tan(45^o)=\tan\pi/4=1$. You can invert this to get
$$\frac{\pi}{4}=\arctan 1.$$
Oh-ho! This gives us a way to come up with a series representation for $\pi$!
Do this:
- Calculate / look up the first four derivatives of the arctan function, and evaluate those derivatives at 1.
- Now you've got what you need to expand $f(1+x)=\arctan(1+x)$ in a Taylor series about $f(1)$. Write that out.
- Set $x=0$ in your Taylor expansion, and you have a series representation for $f(1)=\pi/4$. Based on the terms that you calculated (going up to the term that involves the fourth derivative...) what does it look like the pattern for larger terms will be? Write down the first 8 terms in the series based on the pattern you've discovered with the first couple of terms.
- Now calculate the approximation you get for $\pi$ using the first 2, then the first 4, then the first 8 terms.
Image credits
...is this enough information to let us calculate what $f(x)$ at some other location...say, $x=b$?...Or perhaps even at any location, so that we can write out $f(x)$ purely based on characteristics of the function at $x=a$?? The crudest first approximation with this information might be to say
$$f(x)\approx f(a)$$ We might do a bit better by using the rate of change of the function at $x=a$ which is $f'(a) = \left.\frac{d}{dx}f(x)\right|^{x=a}$. Graphically, this is the slope of a tangent line at $x=a$. So, a slightly better approximation would be to estimate the value of the function as:
$$f(x)\approx f(a) + f'(a)\Delta x=f(a)+f'(a)(x-a).$$
This is certainly better than our first crude approximation, but still not terribly exact. Can we use higher order derivatives to improve this approximation even further??
If the function can be written exactly as a power series in powers of $(x-a)$:
$f(x) = c_0 + c_1(x-a)+c_2(x-a)^2+c_3(x-a)^3+c_4(x-a)^4 ...$$ Try this to find the coefficients $c_n$:
Repeating this procedure we find a general formula for the coefficients of the power series in terms of the 'n'th derivative $f^n$ of the function...
$$c_n = f^n(a)/n!.$$
The resulting power series for $f(x)$ in terms of information we have about the function at $x=a$ is our sought after formula, known as the Taylor series:
The "Taylor expansion of $f(x)$ around $x=a$" means:
$$\begineq f(x) &=& f(a)+f'(a)(x-a)+f''(a)(x-a)^2/2 \\
&&\ \ + f'''(a)(x-a)^3/6+ f''''(a)(x-a)^4/24+...\\
&=& \sum_{n=0}^\infty f^{[n]}(a)\frac{(x-a)^n}{n!}.\endeq$$
where $f^{[n]}(a)$ means the $n$-th derivative of $f$ with respect to x, evaluated at $x=a$. (And the "zero-th" derivative means no derivative at all! Just evaluate the function at $x=a$.) Note the equals sign: This is not an approximation, but an exact result. Though we may need an infinite number of terms to fulfill the precise equality.
The Taylor expansion is so useful because there are many functions
which you can approximate pretty well with just a
few terms from its Taylor expansion.
A function which is analytic for its entire domain is said to be entire. An example is the exponential function (animated at right) expanded in this case about $x=0$.
Madhava of Sangamagrama (c. 1350-c. 1425) was an astronomer in Kerala (India) who came up with series approximations for $\sin(x)$ and other trig functions, which we'd now recognize as Taylor series.
To Taylor expand $f(x)=\sin(x)$ around $x=0$, we need to calculate...
$f(0)=\sin(0)=0;$
$f'(0)=\cos(0)=1;$
$\ f''(0)=-\sin(0)=0;$
$ f'''(0)=-\cos(0)=-1,$ For higher order derivatives, we'll once again cycle through 0,1,0,-1...
Substituting these derivatives into our Taylor formula and expanding in powers of $(x-0)^n=x^n$:
$$\sin(x)=x -x^3/3!+x^5/5!-x^7/7!+x^9/9!-....$$
Graphically, you can see this sequence (slowly) converging to the $\sin$ function...
The graphs shown are.... $\sin(x)$ $x - \frac{x^3}{3!}$ $\sin(x)$ $x - ... + \frac{x^9}{9!}$ $\sin(x)$ $x - ... - \frac{x^15}{15!}$

xkcd
Some crude approximations
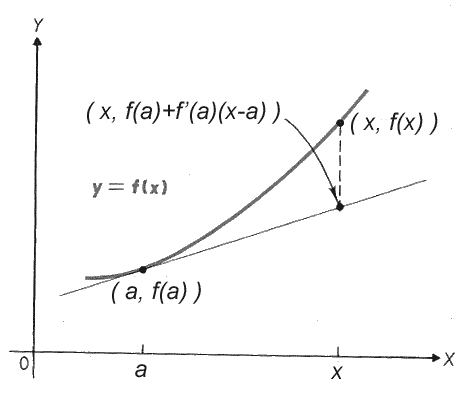
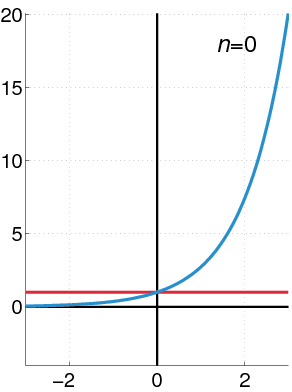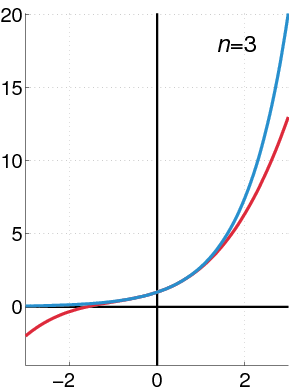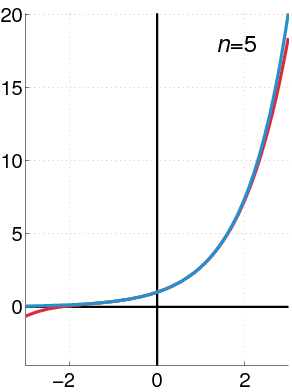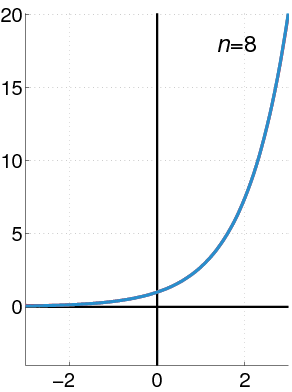 A (real) function which is equal to its Taylor series on some open interval is said to be analytic.
A (real) function which is equal to its Taylor series on some open interval is said to be analytic.
Madhava series for $\sin(x)$
n=3
n=9
n=15
Exercises